FUVEST VESTIBULAR 2006. RESOLUÇÃO DA PROVA DA FASE 2

FUVEST VESTIBULAR 2006.
RESOLUÇÃO DA PROVA DA FASE 2.
Por Professora Maria Antônia Conceição Gouveia
QUESTÃO .01
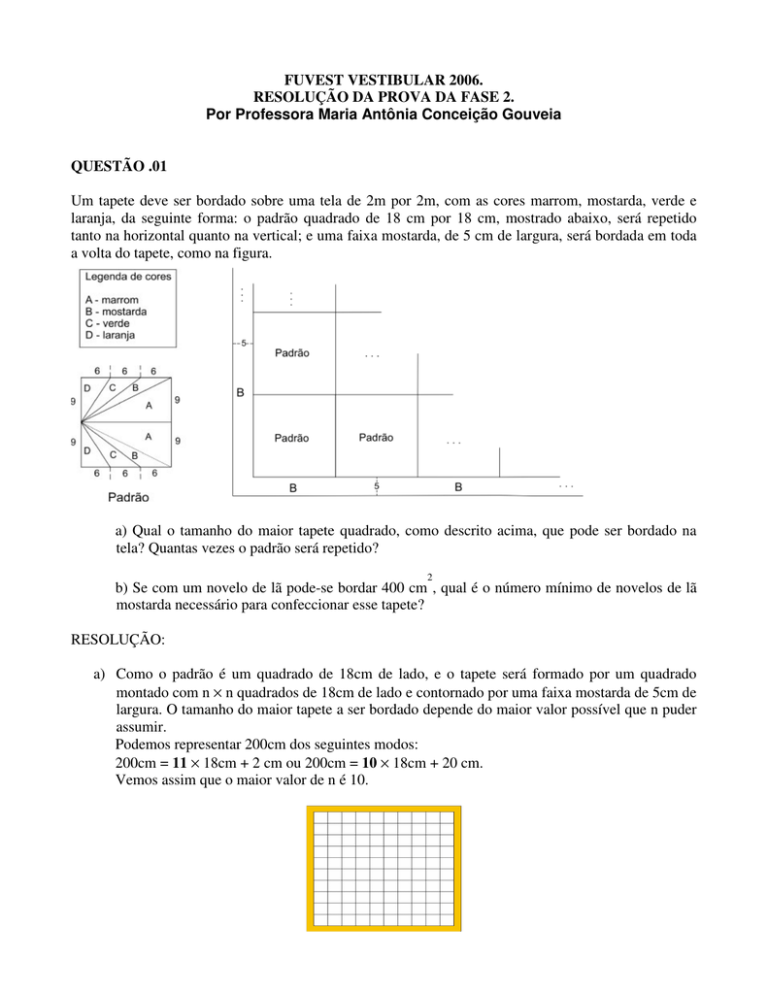
Um tapete deve ser bordado sobre uma tela de 2m por 2m, com as cores marrom, mostarda, verde e
laranja, da seguinte forma: o padrão quadrado de 18 cm por 18 cm, mostrado abaixo, será repetido
tanto na horizontal quanto na vertical; e uma faixa mostarda, de 5 cm de largura, será bordada em toda
a volta do tapete, como na figura.
a) Qual o tamanho do maior tapete quadrado, como descrito acima, que pode ser bordado na
tela? Quantas vezes o padrão será repetido?
2
b) Se com um novelo de lã pode-se bordar 400 cm , qual é o número mínimo de novelos de lã
mostarda necessário para confeccionar esse tapete?
RESOLUÇÃO:
a) Como o padrão é um quadrado de 18cm de lado, e o tapete será formado por um quadrado
montado com n × n quadrados de 18cm de lado e contornado por uma faixa mostarda de 5cm de
largura. O tamanho do maior tapete a ser bordado depende do maior valor possível que n puder
assumir.
Podemos representar 200cm dos seguintes modos:
200cm = 11 × 18cm + 2 cm ou 200cm = 10 × 18cm + 20 cm.
Vemos assim que o maior valor de n é 10.
Cada lado do tapete vai medir 10 × 18cm + 2 × 5cm = 180cm + 10cm = 190cm.
Sendo o tapete montado com n × n quadrados, o padrão será repetido 10 × 10 = 100 vezes.
b)
O tapete tem 100 quadrados do padrão acima ( figura à esquerda) e mais uma moldura do tipo à direita.
A área pintada em mostarda é então:

 6×9
2
2
2
2
2
100 × 2 ×  2  + 190 − 180  cm = (5400+36100-32400)cm = 9100cm .




9100
= 22,75 .
Como com cada novelo são bordados 400cm2 do tapete, o número de novelos será
400
QUESTÃO.02
Um comerciante compra calças, camisas e saias e as revende com lucro de 20%, 40% e 30%,
respectivamente. O preço x que o comerciante paga por uma calça é três vezes o que ele paga por uma
camisa e duas vezes o que ele paga por uma saia.
Um certo dia, um cliente comprou duas calças, duas camisas e duas saias e obteve um desconto de 10%
sobre o preço total.
a) Quanto esse cliente pagou por sua compra, em função de x?
b) Qual o lucro aproximado, em porcentagem, obtido pelo comerciante nessa venda?
RESOLUÇÃO:
Calças
Camisas
Saias
Total
Custo /unidade
x
x
3
x
2
11x
6
Venda
1,2x
 x  1,4x
1,4  =
3
3
 x  1,3x
1,3  =
2
2
Valor p/cliente sem desconto
2,4x
2,8x
3
1,3x
13,9 x
3
a) Como o cliente obteve um desconto de 10%, pagou pela compra: 0,9×
13,9 x
= 4,17x.
3
11x 11x
=
,
6
3
Percentual do total pago pelo cliente em relação ao custo:
(4,17x ) ÷  11x  = 4,17 × 3 = 1,1372727.... o que implica num lucro de 13,73%.
11
 3 
b) Custo de duas unidades de cada peça: 2×
QUESTÃO.03
Uma função f satisfaz a identidade f(ax) = af(x)para todos os números reais a e x. Além disso, sabe-se
que f(4) =2. Considere ainda a função g(x) = f(x−1) +1 para todo o número real x.
a) Calcule g(3).
b) Determine f(x), para todo x real.
c) Resolva a equação g(x) = 8.
RESOLUÇÃO:
4
4
4
x
⇒ f(4) = . f (x ) ⇒ = . f (x ) = 2 ⇒ f(x) = .
x
x
x
2
x -1
3 −1
a) g(x) = f(x−1) +1 ⇒ g(x) =
+1 ⇒ g(3) =
+1 = 2 .
2
2
x
b) f(x) = .
2
x -1
x -1
c) Em g(x) =
+1 fazendo g(x) = 8, temos
+1 = 8 ⇒ x – 1 +2 = 16 ⇒ x = 15.
2
2
Se ax = 4 ⇒ a =
QUESTÃO.04
A reta s passa pela origem O e pelo ponto A do primeiro quadrante. A reta r é perpendicular à reta s, no
ponto A, e intercepta o eixo x no ponto B e o eixo y no ponto C. Determine o coeficiente angular de s
se a área do triângulo OBC for o triplo da área do triângulo OAB.
RESOLUÇÃO:
BC.AO
AB.AO
= 3S OAB =
⇒ BC = 3AB ⇒ AC = 2AB .
2
2
OA
AB
Do triângulo retângulo OAB, temos tgθ =
. Do triângulo OAB, temos tgθ =
⇒
AC
AO
OA AB
=
⇒ AO2 = AB.AC, como AC = 2AB, AO2 = 2 AB2 ⇒ AO = AB 2 .
AC AO
AB
AB
2
2
=
=
⇒ o coeficiente da reta s é
.
Assim tgθ =
AO AB 2
2
2
S BOC =
QUESTÃO.05
Na figura abaixo, O é o centro da circunferência de raio 1, a reta AB é secante a ela, o ângulo β mede
o
3
60 e senα =
.
4
a) Determine sen OÂB em função de AB.
b) Calcule AB.
RESOLUÇÃO:
3
13
3
⇒ cos2α +
= 1 ⇒ cosα =
.
4
16
4
a) Pela Lei dos Senos, aplicada no triângulo OAB, temos:
OB
AB
1
AB
3
3
=
⇒
=
⇒ AB.sen(OÂB) =
⇒ sen(OÂB) =
4
4AB
sen(OÂB) senα
sen(OÂB)
3
4
senα =
b) OÂB = CB̂O − BÔA (propriedade do ângulo externo de um triângulo qualquer) ⇒
3 13
3 1
39
3
.
−
. =
−
sen OÂB = senCB̂O.cosBÔA − senBÔA.cosCB̂O =
2 4
4 2
8
8
Comparando este valor com o obtido no item a:
3
39
3
2
13 + 1
=
−
⇒ AB 3 13 − 1 = 2 3 ⇒ AB =
=
4AB
8
8
6
13 − 1
(
)
QUESTÃO.06
Um torneiro mecânico dispõe de uma peça de metal maciça na forma de um cone circular reto de 15
cm de altura e cuja base B tem raio 8 cm (Figura 1). Ele deverá furar o cone, a partir de sua base,
usando uma broca, cujo eixo central coincide com o eixo do cone. A broca perfurará a peça até
atravessá-la completamente, abrindo uma cavidade cilíndrica, de modo a obter-se o sólido da Figura 2.
Se a área da base deste novo sólido é 2/3 da área de B, determine seu volume.
RESOLUÇÃO:
Como a base do novo sólido 2/3 da base do cone, então a base do cilindro é 1/3 da base do mesmo
cone. Representando como r a medida do raio do cilindro:
2
2
1 r
64
8 3 1 h
225
=   ⇒ r2 =
⇒r=
e =   ⇒ h2 =
= 75 ⇒ h = 5 3
3 8
3
3
3  15 
3
64π .15 1  64 
320 3π
−  π 5 3 = 320π −
=
3
3 3 
9
( )
Vtronco = Vcone maior – Vcone menor =
=
320π (9 − 3 )
.
9

320 3 
 64 
π .
Vcilindro =   15 − 5 3 π =  320 −

3
 3 


Volume
(
)
pedido:
Vtronco
–
Vcilindro
=
=
320π (9 − 3 )
9
–

320 3 
 320 −
π


3


=
2880π − 320 3π − 2880π + 960 3π 640 3π
=
9
9
Resposta:
640 3π
cm3
9
QUESTÃO.07
No paralelogramo ABCD abaixo, tem-se que AD= 3 e DÂB = 30o . Além disso, sabe-se que o ponto P
pertence ao lado DC e à bissetriz do ângulo DÂB .
a) Calcule AP.
b) Determine AB sabendo que a área do quadrilátero ABCP é 21.
RESOLUÇÃO:
a) Sendo a semi-reta AP bissetriz do ângulo DÂB, o triângulo ADP é isósceles.
Aplicando neste triângulo a lei dos cossenos:

3
 ⇒ x2 = 18 + 9 3 ⇒
x2 = 9 + 9 – 2. 3. 3. cos150° ⇒ x2 = 18 – 18.  −

 2 
AP = 3 2 + 3
A + B = 2
2 + 3 = A + B ⇒ A + B + 2 AB = 2 + 3 ⇒ 
⇒
4AB = 3
 3
3
1
1 3 6+ 2
=
A= e B = ⇒ AP = 3 2 + 3 = 3 
.
+

2
2
2
2
2


Escrevendo
(
)
b)
O segmento AH representa a altura do triângulo ADP e do paralelogramo ABCD.
1
9 1 9
A área do triângulo ADB pode ser calculada: SABC = .3.3.sen 150° = . = , bem como por: SABC =
2
2 2 4
3.AH
9
DP.AH 3.AH
3
=
⇒
= 1,5.
= ⇒ AH =
2
2
2
2
4
Como a área do trapézio ABCP é 21, temos:
(AB + PC )AH = 21 ⇒
2
(AB + AB − 3). 3 
(2AB − 3). 1
2
2
2AB − 3 = 28 ⇒ 2AB = 31 ⇒ AB =
 2  = 21 ⇒
2 = 7 ⇒ 2AB − 3 = 7 ⇒
4
31
= 15,5 .
2
QUESTÃO.08
 z -1  1
Determine os números complexos z que satisfazem, simultaneamente, z = 2 e Im
=
1+ i  2
Lembretes: i2 = – 1; se w = a + bi, com a e b reais, então w = a 2 + b 2 e Im(w) = b.
RESOLUÇÃO:
 z = a 2 + b 2
Consideremos z = a+bi ⇒ 
⇒ a 2 + b 2 = 4 (I)
 z = 2
z - 1 (z - 1)(1 − i ) z − 1 − zi + i a + bi − 1 − ai + b − i a − 1 + (b − a − 1)i
=
=
=
=
.
1 + i (1 + i )(1 − i )
2
2
2
b − a −1 1
 z -1  1
Sendo Im
= ⇒ b − a = 2 (II)
 = , então
2
2
1+ i  2
b 2 + (b − 2 )2 = 4
 b = 0 e a = −2

a 2 + b 2 = 4 2b 2 − 4b + 4 = 4 
De I e II temos o sistema 
⇒
⇒ ou
b
−
a
=
2
(
)
b
b
2
=
0


b = 2 e a = 0

b = 0 ou b = 2

Logo z = – 2 ou z = 2i.
QUESTÃO.09
Considere o sistema linear nas variáveis x, y e z.
(
(
) ( )
) ( )
) ( )
 x + cos 2 a y + sen 2 a z = 0

2
2
 x + cos b y + sen b z = 0
 cos 2 c y + sen 2 c z = 0

(
a) Calcule o determinante da matriz dos coeficientes do sistema linear.
b) Para que valores de a, b e c o sistema linear admite soluções não triviais?
c) Calcule as soluções do sistema quando sen2a = 1 e cos2c = 1/5.
RESOLUÇÃO:
1 cos 2a sen 2a  1 cos 2a sen 2a


a) det 1 cos 2 b sen 2 b  = 1 cos 2 b sen 2 b Substituindo a segunda coluna pela sua soma com a
0 cos 2c sen 2c  0 cos 2c sen 2c


1 1 sen 2a
terceira coluna: 1 1 sen 2 b = sen 2c + sen 2a - sen 2 b - sen 2c = sen 2a - sen 2 b
0 1 sen 2c
1 cos 2a sen 2a
1 cos 2 b sen 2 b = (sen a - sen b )(sen a + sen b )
0 cos 2 c sen 2 c
(I)
a −b a +b
c
 e (sen a + sen b ) = 2sen a + b cos a − b  ,
 2   2 
 2   2 
Sendo (sen a - sen b ) = 2sen 
substituindo em (I), temos:
(sen a - sen b)(sen a + sen b)
a+b a−b
a −b a +b
= 2sen 
cos
=
 cos
 . 2sen 
 2   2 
 2   2 
  a − b 
  a + b 
a + b
a +b
a −b
a −b
2sen 
. cos
 = sen 2/ 
.cos 2/ 

.cos
 . 2sen
 2 
 2 
 2 
 2 
  2/ 
  2/ 
1 cos 2a sen 2a 


Logo det 1 cos 2 b sen 2 b  = sen(a – b).sen(a + b).
0 cos 2c sen 2c 


b) Um sistema homogêneo admite soluções não triviais quando o determinante da matriz dos seus
coeficientes é nulo.
Assim: sen(a – b).sen(a + b) = 0 ⇒ sen(a – b) = 0 ou sen(a + b) = 0 que é verdadeira para
(a – b = kπ ou a + b = kπ, com k∈ z) ⇒ ( a = ± b + kπ, com k∈ z).
Resposta: Quando a, b e c são números reais, com a = ± b + kπ, com k∈ z.
c) Se sen2a = 1 e cos2c = 1/5, então cos2a = 0 e sen2c = 4/5.

 x + cos 2 a y + sen 2 a z = 0
x + z = 0


2
2
2
2
 x + cos b y + sen b z = 0 ⇒  x + cos b y + sen b z = 0 ⇒
 cos 2 c y + sen 2c z = 0
 y 4z

 +
=0
5 5
(
(
(
) ( )
) ( )
) ( )
(
) (
(
(
)
) (
) (
)
− z − 4z cos 2 b + sen 2 b z = 0
x = −z


2
2
2
2
x + cos b y + sen b z = 0 ⇒ − z − 4z cos b + 1 − cos b z = 0
 y = −4z
− 5z cos 2 b = 0 ⇒ z cos 2 b = 0


(
) (
)
(
)
(
)
)
Se cos2b ≠ 0, a solução do sistema é S ={(0, 0, 0)} e se cos2b = 0, a solução do sistema é
{(– z , –4z, z) com z ∈R}.
QUESTÃO.10
a) Determine os pontos A e B do plano cartesiano nos quais os gráficos de
12
y=
− 1 e x + y − 6 = 0 se interceptam.
x
b) Sendo O a origem, determine o ponto C no quarto quadrante que satisfaz
AÔB = AĈB e que pertence à reta x = 2.
RESOLUÇÃO:
x = 3 e y = 3
12
12


−1
x 2 − 7x + 12 = 0 
−1
y =
6 − x =
a) 
⇒
⇒
⇒ ou
x
x
x = 3 ou x = 4
x + y − 6 = 0 6x − x 2 = 12 − x
x = 4 e y = 2


Resposta os pontos são: (3,3) e (4,2).
12
− 1 e x + y − 6 = 0 , da reta x = 2, dos segmentos
x
AO , BO e AB temos o triângulo AOB, Sendo AO = 16 + 4 = 2 5 , BO = 9 + 9 = 3 2 e AB =
b) Construindo os gráficos das funções y =
(4 − 3) 2 + (2 − 3) 2 = 2 . Determinando a natureza do triângulo AOB:
2
2
2
(2 5 ) = ( 2 ) + (3 2 )
⇒ 20 = 20 ⇒ AOB é retângulo de hipotenusa AO , cujo ponto médio é M =
(2,1).
Traçando o gráfico da circunferência de centro em M e raio
5 : (x – 2)2 +(y – 2)2 = 5,
B
3
A
2
O
3
Vemos que ela intercepta a reta x = 2 no ponto C = ( 2, 1 –
4
5 ).