PROBABILIDADES As aplicações iniciais referiam-se

1
4
PROBABILIDADES
As aplicações iniciais referiam-se quase todas a jogos de azar. O ponto de
desenvolvimento da teoria das probabilidades pode ser atribuído a Fermat (1601-1665) e
Pascal (1623-1662). Atualmente os governos, as empresas, as organizações profissionais
incorporam a teoria das probabilidades em seus processos de deliberações.
A utilização das probabilidades indica que existe um elemento de acaso, ou incerteza,
quanto à ocorrência ou não de um evento futuro. Mediante determinada combinação de
julgamento, experiência e dados históricos é possível dizer quão provável é a ocorrência de
determinado evento futuro.
A previsão da procura de um produto novo, o cálculo dos custos de produção, a
previsão do malogro de safras, a compra de apólices de seguro, a contratação de um novo
empregado, o preparo de um orçamento, a avaliação do impacto de uma redução(aumento) de
impostos sobre a inflação; contém algum elemento de acaso.
As probabilidades são úteis porque ajudam a desenvolver estratégias. Assim alguns
motoristas parecem demonstrar uma tendência para correr a grandes velocidades se acham
que há pouco risco de serem apanhados, os investidores sentem-se mais inclinados a aplicar
seu dinheiro se as chances de lucros são boas, carregaremos capa ou guarda-chuva se houver
grande probabilidade de chuva; uma empresa pode sentir-se inclinada a negociar se houver
forte ameaça de greve; mais inclinado a investir num novo equipamento se há boa chance de
ganhar dinheiro; ou a contratar um novo funcionário que pareça promissor.
AS PROBABILIDADES SÃO UTILIZADAS PARA EXPRIMIR A CHANCE DE
OCORRÊNCIA DE DETERMINADO EVENTO.
CARACTERIZAÇÃO DE UM EXPERIMENTO ALEATÓRIO
Cada experimento poderá ser repetido sob as mesmas condições
indefinidamente
Não se conhece um particular valor do experimento “a priori”, porém podemos
descrever todos os resultados possíveis – as possibilidades.
Quando o experimento for repetido um grande número de vezes, surgirá uma
s
regularidade, uma estabilidade da fração f =
n
f = freqüência relativa, n = número de repetições, s = número de sucessos de um
particular resultado estabelecido antes da realização.
ESPAÇO AMOSTRAL: É o conjunto (S) de todos os possíveis resultados de um
experimento aleatório (E).
Exemplo:
E = { jogar um dado e observar a face de cima }
S = { 1, 2, 3, 4, 5, 6}
E = { jogar duas moedas e observar o resultado}
S = { (c,c), (c,k), (k,c), (k,k) }
山村
2
EVENTO : é um conjunto de resultados do experimento (subconjunto de S).
φ = evento impossível
S = evento certo
A ∪ B ⇒ ocorre o evento A ou o B ou ambos ocorrem
A ∩ B ⇒ ocorrem A e B
A
⇒ é o evento que ocorre se A não ocorre
Exemplos:
1.
2.
E = { jogar três moedas e observar os resultados }
A = { ocorrer pelo menos duas caras }
R: E = { (c,c,c), (c,c,k), (k,c,c), (c,k,c), (k,k,k), (k,c,k), (k,k,c), (c,k,k) }
A = { (c,c,c), (c,c,k), (c,k,c), (k,c,c) }
E = { lançar um dado e observar a face de cima }
B = { ocorrer um múltiplo de 2 }
R: E = { 1, 2, 3, 4, 5, 6}
B = { 2, 4, 6}
EVENTOS MUTUAMENTE EXCLUSIVOS: não ocorrem simultaneamente A e B
(A∩B= φ )
Exemplo:
E = {.jogar um dado e observar o resultado }
A = { ocorrer um número par }
B = { ocorrer um número ímpar }
A∩B = φ
E = { 1, 2, 3, 4, 5, 6}
A = { 2, 4, 6}
B = { 1, 3, 5}
DEFINIÇÃO DE PROBABILIDADE:
Dado um espaço S, P(A) = probabilidade de um evento A – é uma função definida em
S que associa a cada evento um número real, satisfazendo os axiomas:
1.
2.
3.
4.
5.
0 ≤ P(A) ≤ 1
P(S) = 1
P(A ∩B) = φ ⇒
P( φ ) = 0
P(A∩B) ≠ φ
P(A ∪ B) = P(A) + P(B)
⇒
P(A∪B) = P(A) + P(B) – P(A∩B)
ESPAÇOS AMOSTRAIS FINITOS EQUIPROVÁVEIS
P(A) =
número.de.casos. favoráveis
número.total.de.casos
山村
3
REGRAS DE PROBABILIDADES
Eventos mutuamente excludentes (A ou B ocorrerá)
P(A∪B) = P(A) + P(B)
P(A∩B) = φ
Eventos não mutuamente excludentes (A ou B ou ambos ocorrerão)
P(A∪B) = P(A) + P(B) – P(∩B)
Eventos independentes
P(A∩B) = P(A) P(B)
Eventos dependentes
P(A∩B) = P(B) P(AB) ou P(A) P(BA)
Dois ou mais eventos dizem-se independentes se a ocorrência ou a não ocorrência de
um não influencia a ocorrência do(s) outro(s).
Exercícios:
1. Jogam-se duas moedas equilibradas. Qual a probabilidade de darem cara? (1/4)
2. Um terço dos eleitores de certa comunidade é constituído de mulheres, e 40% dos
eleitores votaram na última eleição presidencial. Supondo que esses dois eventos
sejam independentes, determine a probabilidade de escolher aleatoriamente um
eleitor da lista geral, que seja mulher e que tenha votado na última eleição. (0.133)
3. Em 25% das vezes X chega em casa tarde para jantar. Por outro lado, o jantar atrasa
10% das vezes. Se não há qualquer relacionamento entre os atrasos de X e os
atrasos do jantar, qual a probabilidade de ocorrerem ambos os atrasos? (0.025)
QUANDO OS EVENTOS NÃO SÃO INDEPENDENTES
Exemplo:
Suponha duas urnas com fichas. A primeira Y contém 8 vermelhas e 2 brancas. A
Segunda Z contém 5 vermelhas e 5 brancas. Vamos extrair uma ficha vermelha de cada uma
das urnas. Observe que depende (condicional) de qual seja a urna escolhida.
P(V/ Z) = 5/10
P(B/Y) = 2/10
P(B/Z) = 5/10
Suponha que as duas urnas sejam indistinguíveis e que a probabilidade de escolher
qualquer delas seja ½. Qual a probabilidade de extrair uma ficha vermelha da urna Z?
P(Z) = ½
P(V/Z) =5/10
⇒ P(Z)P(V/Z) = (½).(5/10) = 1/4
Calcule P(Y)P(V/Y)
(0.40)
PROBABILIDADE DE OCORRÊNCIA DE AO MENOS UM DE DOIS EVENTOS
A.
mutuamente excludentes: P(A∪B) = P(A) + P(B)
山村
4
Exercício:
1)
2)
Determine a probabilidade de aparecer cinco ou seis numa jogada de um dado
equilibrado (2/6)
Determine a probabilidade de extração de uma carta de copas ou de uma carta
de paus de um baralho de 52 cartas (1/2)
B.
Não são mutuamente excludentes:
P(A∪B) = P(A) + P(B) – P(A∩B) ⇒ P(A∪B) = P(A) + P(B) – P(A).P(B)
Exercício:
1.
2.
3.
Determine a probabilidade de extração de uma carta de paus ou um dez de um
baralho de 52 cartas (16/52)
Uma urna contém 15 bolas do mesmo raio, enumeradas de 1 a15. Sendo A e B
os eventos. Retirar uma bola múltiplo de 3 ou 4 (7/15)
Idem, retirar uma bola múltiplo de 5 ou 4 ( 2/5)
Teorema de Bayes : Seja A1, A2, A3 ...........An, n eventos mutuamente exclusivos tais
que A1∪A2∪......An = S. Seja P(Ai ) as probabilidades conhecidas dos vários eventos, e B um
evento qualquer de S tal que são conhecidas todas as probabilidades condicionais P(B/Ai)
Então, para cada “i”, tem-se:
P( Ai ).P( B / Ai )
P(Ai/B) =
P( A1).P( B / A1) + P( A2).P( B / A2) + .... + P( An).P( B / An)
O teorema de Bayes é uma técnica utilizada para revisar estimativas probabilísticas
iniciais com base em dados amostrais.
Exemplo 1: Sejam as urnas:
u1
u2
u3 e bolas nas cores:
pretas
3
4
2
Brancas
1
3
3
Vermelhas 5
2
3
Escolheu-se uma urna ao acaso e dela extraiu-se uma bola ao acaso, verificando-se que
ela é branca. Qual a probabilidade da bola ter vindo da urna 2 ? e da 3 ?
P(u1) = P(u2) = P(u3) = 1/3
P(br/u1) = 1/9; P(br/u2) = 3/9= 1/3; P(br/u3) = 3/8
P(u2/br) =
P(u2/br) = ? P(u3/br) = ? (27/59)
P(u 2).P(br / u 2)
P(u1) P(br / u1) + P(u 2) P(br / u 2) + p (u 3) P(br / u 3)
1 / 3.1 / 3
= 24/59
1 / 3.1 / 9 + 1 / 3.1 / 3 + 1 / 3.3 / 8
P(u3 ).P(br / u3 )
27
P(u3|br) =
=
P(u1) P(br / u1) + P (u 2) P(br / u 2) + p(u 3) P(br / u 3) 59
=
山村
5
Exercícios:
1. De um baralho de 52 cartas, escolha aleatoriamente uma carta que seja:
A = {a carta é de ouros} (13/52)
B = {a carta é uma figura} (3/13)
2. Lance um dado e uma moeda.
a) Construa o espaço amostral
b) Enumere os seguintes eventos:
A = {coroa, marcado por número par}
B = {cara, marcado por número ímpar}
C = {múltiplos de 3}
3. Determine a probabilidade de cada evento:
a) Um número par aparece no lançamento de um dado
b) Um rei aparece ao extrair-se uma carta de um baralho
c) Pelo menos uma cara aparece no lançamento de 3 moedas
d) Duas copas aparecem ao retirarem-se duas cartas de um baralho
e) Uma carta de copas e uma de ouros aparecem ao extraírem-se duas cartas de
um baralho.
4. Um número inteiro é escolhido aleatoriamente dentre os números 1, 2, 3,... 50.
Qual a probabilidade de:
a) Número ser divisível por 5
b) Terminar em 3
c) Ser divisível por 6 ou por 8
5. Qual a probabilidade de sair um rei ou uma carta de copas, quando retiramos uma
carta de um baralho?
6. Dois dados são lançados simultaneamente. Qual a probabilidade:
a) A soma ser menor que 4
b) A soma ser 9
c) O primeiro resultado ser menor que o segundo
7. Uma urna contém 5 bolas brancas e 6 pretas. Três bolas são retiradas. Calcule a
probabilidade de:
a) Todas pretas
b) Exatamente uma branca
c) Ao menos uma preta
8. Numa classe existem 5 alunos do quarto ano, 4 do segundo ano e 3 do terceiro ano.
Qual a probabilidade de serem sorteados 2 alunos do segundo ano, 3 do quarto ano
e dois do terceiro ano?
9. Extrai-se uma só carta de um baralho de 52. Determine a probabilidade de obter:
a) Um valete
b) Uma figura
c) Uma carta vermelha
d) Uma carta de ouros
e) Um dez de paus
f) Um 9 vermelho ou um 8 preto
10. Há 50 bolas numa urna, distribuídas como segue:
Cor:
azul vermelho
laranja
verde
Quantidade:
20
15
10
5
=
50
山村
6
Misturam-se as bolas e escolhe-se uma. Determine a probabilidade de a bola
escolhida ser:
a) Verde
b) Azul
c) Azul ou verde
d) Não vermelha
e) Vermelha ou verde
f) Amarela
g) Não amarela
11. No lançamento de dois dados, determine a probabilidade de se obter:
a) A soma dos pontos igual a 10 (3/36)
b) O número de pontos de uma das faces igual ao dobro do número da outra face
(6/36)
c) A soma dos pontos igual a 13 (0)
d) Obter a soma dos pontos menor ou igual a 12 (36/36=1)
e) Obter pontos iguais (6/36)
f) A soma ser 8 (5/36_
g) A soma ser um número primo (15/36)
h) A soma das faces ser 8 ou um número primo (20/36)
i) A soma ser 6 ou 8 (5/18)
12. Uma carta é retirada de um baralho de 52 cartas. Determine a probabilidade de ela
ser:
a) Uma dama ou carta de copas (4/13)
b) Ser vermelha ou ser figura (32/52)
c) Sair rei ou uma carta de espadas (4/13)
d) Ser figura ou carta de paus (11/26)
13. Uma caixa contém 10 bolas, das quais 3 são vermelhas, 5 são azuis e duas são
pretas. Retira-se uma bola ao acaso. Qual a probabilidade de:
a) Ser vermelha (3/10)
b) Não ser vermelha (7/10)
14. Se a probabilidade de um atirador acertar ao alvo é 4/7, qual a probabilidade dele
errar o alvo? (3/7)
15. Uma caixa contém 20 bolas, das quais 12 são brancas, 5 são pretas e 3 são
amarelas. Retira-se uma bola ao acaso, qual a probabilidade de:
a) Ser amarela (3/20)
b) Ser preta (1/4)
c) Não ser amarela (17/20)
d) Não ser preta (3/4)
e) Não ser branca (2/5)
16. Uma urna tem 15 bolas, das quais 6 são brancas e 9 são pretas. Retiradas duas
bolas ao acaso sem reposição, qual a probabilidade de se obter:
a) Duas bolas pretas (12/35)
b) Pelo menos uma bola branca (23/35)
17. Considere um grupo de 20 estudantes, dos quais 13 são homens e 7 são mulheres.
Cinco homens e 3 mulheres usam óculos. Escolhido um estudante ao acaso,
calcule a probabilidade de:
a) O estudante escolhido não usar óculos (12/20)
b) O estudante escolhido ser mulher (7/20)
山村
7
c) Do estudante não usar óculos e ser mulher (4/7)
18. Qual a probabilidade de, no lançamento de um dado branco e um dado amarelo,
ocorrer 4 no dado branco e face 6 no dado amarelo. (1/36)
19. Lançam-se um dado e uma moeda. Qual a probabilidade de se obter face 3 no dado
e coroa na moeda. (1/12)
20. Numa urna há 4 bolas brancas e 6 bolas pretas. Qual a probabilidade de retirarmos
sucessivamente uma bola branca e uma preta com reposição? (24/100)
21. Num sorteio, a caixa A contém 5 bolas brancas e 5 bolas pretas; a caixa B contém
10 bolas azuis e 40 bolas verdes; na caixa C há 15 amarelas e 4 vermelhas. Se
sortearmos uma bola de cada caixa, qual é a probabilidade serem: branca da caixa
A, verde da caixa B e amarela da caixa C? (8/25)
22. Se retirarmos aleatoriamente uma carta de um baralho de 52 cartas, qual a
probabilidade de ser um 7 ou um ás? (8/52)
23. Em um final de torneio de tiro ao alvo a probabilidade de X acertar no alvo é 1/2 e
a de Y é 3/5. Qual a probabilidade de o alvo ser atingido, se ambos atirarem no
alvo. (4/5)
24. Dois amigos foram caçar. Sabe-se que um deles tem 45% de probabilidade de
acertar qualquer caça, enquanto o outro tem 60%. Qual a probabilidade de em cada
tiro disparado:
a) Ambos acertarem na caça (27%)
b) Nenhum acertar na mesma caça (22%)
c) A caça ser atingida (78%)
d) Apenas um acertar a caça (51%)
25. A tabela descreve os hóspedes registrados pelo período de uma semana num hotel
de Curitiba. A distribuição segue de acordo com o sexo e a idade:
Hóspedes hotel PP, período XX
Sexo
Idade
Total
Feminino
Masculino
Abaixo de 20 anos
20
15
35
Entre 20 e 40 anos
65
150
215
Acima de 40 anos
50
95
145
Total
135
260
395
Se um hóspede é aleatoriamente escolhido, qual a probabilidade de:
a) Ser mulher? (0,342)
b) Ser mulher e ter acima de 40 anos? (0,127)
c) Ser homem e ter menos de 20 anos? (0,0038)
d) Ser mulher entre 20 e 40 anos? (0,165)
e) Ser homem e ter menos de 40 anos? (0,418)
f) Ter entre 20 e 40 anos? (0,589)
山村
8
5
DISTRIBUIÇÕES DE PROBABILIDADE
É uma distribuição de freqüências para os resultados de um espaço amostral.
(as “f” são relativas – probabilidades) Mostra a proporção das vezes em que a v.
aleatória tende a assumir cada um dos diversos valores.
Variável discreta: Em Estatística aplicada à Administração, tais dados ocorrem
tipicamente através de processos de contagem, por isso, tais valores são e geralmente
expressos por números inteiros.
Exemplos: no de pessoas por domicílio, no de peças defeituosas encontradas em um
lote, número de acidentes. Os específicos modelos discretos de probabilidade são as
distribuições de probabilidade binomial, a de Poisson. e (hipergeométrica).
Variável contínua: assume qualquer valor fracionário ao longo de um intervalo
específico de valores. Os dados são gerados pelo processo de medição.
Exemplos: pesos de caixas de laranjas, alturas de pinheiros, duração de uma conversa
telefônica, tempo decorrido antes da primeira falha de um dispositivo, número médio de
pessoas por domicílio em uma grande cidade.
São retratadas por uma curva de probabilidade (normal) e (exponencial).
VALOR ESPERADO (E(X)) ou média: é a média ponderada de todos os possíveis
valores da variável com os respectivos valores de probabilidade tomado como pesos.
E(X) = ∑ XP( X )
VARIÂNCIA: quadrado do desvio padrão
2
2
Var(X) = ∑ X . P ( X ) - [∑ X .P ( X )] = E(X2) – [E(X)]2
Propriedades da média (v.a.discreta)
1. A média de uma constante é a própria constante
E (k ) = ∑ kp( x) = k ∑ p( x) = k
2. Multiplicando uma variável aleatória x por uma constante, sua média fica multiplicada
por essa constante:
E[kx]= ∑ kxp( x) = k ∑ xp( x) = kE[ x]
3. A média da soma de duas v. a. é a soma ou diferença das médias
E[ x ± y ] = ∑∑ ( xi ± y j ) = ∑∑ xi p( xi , y j ) ± ∑∑ y j p( xi , y j ) =
i
∑ x ∑ p( x , y
i
i
i
j
i
j
i
i
i
i
) ± ∑ yi ∑ p ( xi , y j ) = ∑ xi p ( xi ) ± ∑ yi p ( y j ) = E[ x] ± E[ y ]
j
i
i
j
4. A média do produto de duas v. a. independentes é o produto das médias
E[ xy ] = ∑∑ xi y j p ( xi , y j )
i
j
i
j
E[ xy ] = ∑∑ xi y j p ( xi ) p ( y j ) , pois x e y são independentes
E[ xy ] = ∑ xi p ( xi )∑ y j p ( y j ) = E[ x]E[ y ]
i
j
山村
9
Propriedades da variância (v.a.discreta)
1. A variância de uma constante é zero
σ ( k ) 2 = E[(k − µ )2 ] = E[(k − k )2 ] = 0
2. Multiplicando-se uma v.a. por uma constante, sua variância fica multiplicada pelo
quadrado da constante
σ 2 ( kx ) = E[(kx − µ( kx ) )2 ] = E[k 2 ( x − µ( x ) )2 ] = k 2 E[( x − µ( x ) )2 ] = k 2σ 2 ( x )
3. Somando-se uma constante à uma v.a. sua variância não se altera
σ 2 ( x ± k ) = σ 2 ( x) ± σ 2 (k ) = σ 2 ( x) pois σ 2 (k ) = 0
4. A variância da soma de duas v.a. independentes é a soma das respectivas variâncias
σ 2 ( x ± y ) = E[[( x ± y ) − ( µ x ± µ y )]2 ] = E[[( x − µ x ) ± ( y − µ y )]2 ] =
E[( x − µ x ) 2 ± 2 E[( x − µ x )( y − µ y )] + E[( y − µ y )]2
mas, E[( x − µ x )( y − µ y )] = E[( x − µ x ) E ( y − µ y )] = COVxy = 0 , pois x e y são
independentes.
Onde
COVxy =covariância
entre
x
e
y.
portanto:
σ ( x ± y ) = σ ( x) + σ ( y )
2
2
2
Covariância: mede o grau de dispersão conjunta entre duas variáveis aleatórias.
COVxy = E[( x − µ x )( y − µ y )] , desenvolvendo, temos: COVxy = E[ xy ] − µ x µ y
1. Demanda diária de aluguel de caminhonetes durante de um período de 50 dias
Demanda possível (X )
Número de
dias ( f )
3
3
7
4
12
5
14
6
10
7
4
8
50
Determine a probabilidade de serem solicitadas exatamente:
a)
Sete caminhonetes em um dia aleatoriamente escolhido.
b)
Serem solicitadas seis ou mais
c)
Valor médio a longo prazo (E(X) = 5,66)
d)
A variância (1,74)
2. O número de caminhões que chegam por hora, a um depósito segue a tabela abaixo.
Calcular o número de chegadas por hora X e a variância dessa distribuição.
Chegadas de caminhões por hora a um depósito
Número de caminhões X
0
1
2
3
4
5
6
Probabilidade
0.05 0.10 0.15 0.25 0.30 0.10 0.05
P(X)
E(X)=3,15 var(X)= 2,13
山村
10
Uma das aplicações de E(X) é na tomada de decisão no risco. A decisão em situação
de risco envolve os seguintes elementos:
- Um número finito de alternativas, entre os quais uma decisão deve ser tomada.
- Um certo número de estados da natureza, cujas probabilidades de ocorrência
podem ser previstas.
- Um certo número de conseqüências, resultando da influência de cada estado da
natureza sobre cada alternativa. O risco da alternativa é medido pela diferença
entre os estados mais favorável e desfavorável da natureza.
Exemplo:
1. Uma pessoa tem duas alternativas: aceitar um prêmio de $ 100 (A); receber um
pagamento de $ 200, se uma moeda cair cara, ou não receber nada, se a moeda cair
coroa (B). Determine o pagamento esperado.
Estados
natureza
da
Cara
Coroa
P(x)
Alternativas
A - Aceitar o
B – correr o
prêmio
risco
0,5
100
200
0,5
100
0
E(A)=100
E(B)=0,5x200+0,5x0=100
Os riscos são para as alternativas:
R(A)=100-100=0
R(B)=05x200-0,5x0=100
Portanto, As expectativas de pagamentos são iguais, entretanto a alternativa A não
apresenta risco, ao passo que a alternativa B apresenta um risco considerável.
2. Uma pessoa pode comprar um bilhete de loteria que custa $ 100 e lhe dá uma
oportunidade em um milhão de ganhar o prêmio de 10 milhões. Quais as expectativas
de pagamento e os riscos?
Estados
natureza
Ganha
prêmio
Não ganha
da
o
P(x)
1
1.000.000
999.999
1.000.000
Alternativas
A – Recusar a
B – Aceitar a
loteria
loteria
100
10.000.000
100
0
E(A)=100
1
999.999
x10.000.000 −
x0 = 10
1.000.000
1.000.000
A alternativa A é preferível à alternativa B. O risco da alternativa A é R(A)=1001
999.999
100=0; R(B)=
x10.000.000 −
x0 = 10
1.000.000
1.000.000
E(B)=
3. Uma pessoa pode escolher entre dois investimentos: A: ações de uma indústria que
tem, no passado, dado 30% de lucros; B: ações de uma nova companhia petrolífera
que está realizando prospecções numa região onde, em média, uma concessão em três
山村
11
tem obtido quantidades comerciais de óleo; em se obtendo óleo, o retorno sobre o
investimento é de 70%; senão, é de 10%. Quais as expectativas de pagamento e os
riscos?
Estados
natureza
Descobre
petróleo
Não descobre
da
P(x)
Alternativas
A - Aceitar o
B – correr o
prêmio
risco
1/3
30%
70%
2/3
30%
10%
As expectativas de pagamento são:
E(A)=30%;
1
2
E(B)= x70% + x10% = 30% ; As expectativas são iguais. Os riscos são:
3
3
R(A)=30%-30%=0
1
2
R(B)= x70% − x10% = 16, 7% . Portanto a alternativa B é mais arriscada.
3
3
4. Sabe-se que a demanda semanal Z de certa mercadoria tem a distribuição de
probabilidade:
Demanda (Z)
0
1
2
3
4
5 6 ou mais
P(Z)
0,05 0,10 0,25 0,30 0,20 0,10
0 1,00
A mercadoria é comprada a $ 2.500, por unidade, e vendida a $ 3.700 durante a
semana em questão: na semana seguinte, a mercadoria é considerada resíduo e vendida a
$ 500. A embalagem custa $ 200 por unidade vendida na semana. Qual a quantidade ideal
Q a ser estocada?
Solução: Se Z ≤ Q, temos:
Faturamento proveniente da venda de mercadoria nova: $ 3.700 Z
Custo da embalagem:
$ -200 Z
Faturamento proveniente da venda de resíduos:
$ 500(Q-Z)
Custo da mercadoria comprada:
$ -2.500Q
Portanto, o pagamento obtido é: 3.000Z – 2.000Q
Se Z>Q, o pagamento obtido é: 1.000Q
A matriz de pagamentos está resumido no quadro seguinte. Como exemplos de cálculo
de pagamentos, façamos:
Z=2, Q=3; então o pagamento é: 3.000x2 – 2.000x3= 0
Z=3, Q=2; então o pagamento é: 1.000x2= 2.000
Calculando a expectativa de pagamento, ou lucro esperado, de cada alternativa:
E(Q=0)=0
E(Q=1)=-2x0,05+1x0,95=0,85
E(Q=2)=-4x0,05-1x0,10+2x085=1,40
E(Q=3)=-6x0,05-3x0,10+0x0,25+3x0,60=1,20
E(Q=4)=-8x0,05-5x0,10-2x0,25+1x0,30+4x0,30=0,10
E(Q=5)=-0,10x0,05-7x0,10-4x0,25-1x0,30+2x0,20+5x0,10=-1,60
Portanto, a alternativa preferível é a de estocar Q=2 unidades, que conduz à melhor
expectativa de pagamento E(Q=2)=1,40=$1.400
山村
12
Matriz de pagamentos (em milhares)
Estados
da natureza
Q
=0
Deman
da A
0
1
2
3
4
5
6
P
(Z)
0
,05
0
,10
0
,25
0
,30
0
,20
0
,10
0
=1
=2
2
1
Alternativas
Estocar Q
Q
=3
=4
4
6
1
3
2
Q
=5
1
2
1
2
10
7
4
1
2
1
2
5
1
2
5
1
8
5
2
山村
13
Exercícios
1)
2)
3)
4)
5)
6)
7)
8)
9)
Uma confeitaria produz 5 bolos em determinado dia. As probabilidades de vender
nenhum, um dois, três, quatro ou cinco valem respectivamente 1%, 5%, 20%, 30%, 29%
e 15%. O custo total de produção de cada bolo é de 10 unidades monetárias. e o preço
unitário de venda é 20 u. m. Calcule o lucro médio, e o desvio padrão. (15,2; 22.91)
Um negociante espera vender um automóvel até sexta-feira. A expectativa de que
venda na segunda-feira, é de 50%. Na terça-feira é de 30%, na quarta-feira é de 10%, na
quinta-feira é de 5% e na sexta-feira é de 5%. Seu lucro é de 3 000 um se vender na
segunda-feira e diminui 40% cada dia. Calcule o valor esperado de lucro deste
negociante nesta venda. (2 199,84)
Um produto deve ser lançado no mercado no próximo ano. A expectativa do
departamento de marketing de que o projeto seja bem sucedido é de 80%. Neste caso, o
retorno esperado em sua vida útil é de 100.u. m. Se isto não acontecer, o prejuízo deve
chegar a 50. u. m. Calcule o lucro médio, a variância e o desvio padrão. (70; 3.600; 60)
O trem do metrô para no meio de um túnel. O defeito pode ser na antena receptora ou
no painel de controle. Se o defeito for na antena, o conserto poderá ser feito em 5
minutos. Se o defeito for no painel, o conserto poderá ser feito em 15 minutos. O
encarregado da manutenção acredita que a probabilidade de o defeito ser no painel é de
60%. Qual é a expectativa do tempo de conserto? (11 minutos)
Um vendedor prepara quatro visitas e espera vender 1000 u. m. em cada uma delas. A
expectativa de vender em cada cliente é de 80%, independentemente. Qual é o valor
esperado de vendas deste vendedor? (3.200)
Uma máquina fabrica placas de papelão que podem apresentar nenhum, um, dois, três
ou quatro defeitos, com probabilidade 90%, 5%, 3%, 1% e 1%, respectivamente. O preço
de venda de uma placa perfeita é 10u.m. e a medida que apresenta defeitos, o preço cai
50% para cada defeito apresentado. Qual é o preço médio de venda destas placas? 9,34
Um investidor julga que tem 0,40 de probabilidade de ganhar $ 25 000 e 0,60 de
probabilidade de perder $ 15 000 num investimento. Determine o ganho esperado.
($1000)
Um empreiteiro faz as seguintes estimativas: prazo de execução 10, 15 e 22 dias com
as respectivas probabilidades de: 0,30, 0,20 e 0,50. Determine o prazo esperado para a
execução da obra, de acordo com estas estimativas.(17 dias)
Os registros de uma grande cidade mostram a distribuição de candidatos para
trabalhos não qualificados, durante o tempo em que se encontram desempregados.
Duração do
desemprego
0
1
2
3
4
5
6
7
8
9-12
(semanas)
oporção de candidatos 0,25 0,20 0,15 0,10 0,10 0,05 0,04 0,03 0,02 0,06
Qual a duração esperada de desemprego de um candidato? Determine o desvio padrão.
10)
Uma urna contém 400 notas de $ 5,00 e 100 notas de $ 10,00. Qual o lucro esperado?
(6)
11)
Uma companhia de implementos agrícolas fixou a data para sua exposição anual e
precisa decidir se a exposição será feita em recinto fechado ou a céu aberto. Julga ela
que, se a exposição for feita a céu aberto, e se não chover, poderá ganhar $6.000,00
líquido. Se chover, entretanto, a exposição a céu aberto renderá somente $ 1.000,00. Por
outro lado, se a exposição for feita em recinto fechado, a companhia espera ganhar
$2.000,00, se chover, e $3.000,00, se não chover. Se a probabilidade de chuva é de 0,50,
山村
14
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
calcule o lucro esperado para ambos os tipos de exposição e escolha o tipo que
proporcione o máximo lucro.
No exercício anterior, a probabilidade de chuva é de 0,90.
Uma seguradora paga o preço integral de um carro em caso de perda total. Para um carro
no valor de $ 40.00,00 é cobrado uma taxa de $ 1500,00. A probabilidade de que um
carro tenha perda total é de 3%. Quanto espera a seguradora ganhar por carro segurado?
(300)
As probabilidades de que haja 1, 2, 3, 4 ou 5 pessoas em cada carro que vá ao litoral num
sábado são, respectivamente: 0,05; 0,20; 0,45; 0,25 e 0,05. Qual é o número médio de
pessoas por carro? Se chegam no litoral 500 carros por hora, qual é o número esperado
de pessoas, em 8 horas de contagem? (3,05: 12.200)
O quadro abaixo representa o registro da qualidade do produto PP da fábrica PPY.
Calcule a média de defeitos esperado e o desvio padrão. (0,75; 1,2)
Nº de defeitos
0
1
2
3
4
5 6 ou mais
Percentagem de produtos 0,60 0,22 0,08 0,05 0,03 0,02
0
Um jogo um estádio de futebol, a lanchonete pode esperar lucrar $ 600 com a venda
de cachorro-quentes se o dia for ensolarado, mas só $ 300 se o dia estiver encoberto e $
100 se chover. As probabilidades para esses eventos são 0,6; 0,3 e 0,1. Qual é o lucro
esperado? (460) Se for feito um seguro de $450 e o custo do seguro for de $ 100, qual
será o lucro esperado?(405)
Um lojista mantém extensos registros de vendas diárias de um aparelho. O quadro a
seguir dá o número x de aparelhos vendidos em uma semana e a respectiva probabilidade
p(x)
Número x
0 1
2
3
4
5
P(x)
0,1 0,1 0,2 0,3 0,2 0,1. Se é de R$ 20,00 o lucro por unidade
vendida, qual o lucro esperado nas vendas de uma semana? (54)
Os analistas da corretora de valores definiram os possíveis cenários da rentabilidade
do mercado de ações para os próximos 12 meses: ruim, regular, bom e excelente. Pelo
consenso do grupo de analistas, as rentabilidades e suas probabilidades associadas para o
cenário estão registradas.
Rendabilidade
probabilidade
Ruim
-10%
10%
Regular
0%
20%
Bom
+12%
40%
Excelente
+25%
30%
Determine o valor esperado (11,30%)
O seguro de vida para pessoas com menos de 40 anos pago pela Seguradora FF é
$200.000,00. Para comprar esse seguro, a pessoa necessita pagar $600 por ano. Se a
probabilidade de morte de uma pessoa com menos de 40 anos é 0,1% pede-se determinar
a expectativa de lucro anual da seguradora. (400,60)
Um lago de areia, numa quermesse escolar para angariar fundos, apresenta 25 pacotes
com valor unitário de $ 1, 5 pacotes valendo $ 5 cada um e 1 pacote valendo $ 10.
Quanto gostaria de pagar para ter uma chance nesta pescaria, se quisesse ter um prêmio
Um fabricante de pneus de automóveis conservou os registros de qualidade de seu no
valor daquilo que você gastou? (1,94)
Um produto e obteve o seguinte quadro de valores baseado nos últimos 6 meses de
produção:
Número de defeitos
0
1
2
3
4
5
山村
15
Percentagem de pneus
60
22
8
5
3
2
Calcule a média de defeitos e o desvio padrão. (0,75; 1,2)
22) Um investidor não sabe se investe $ 10000 de sua herança numa ação que lhe foi
recomendada ou se aplica num título de poupança que lhe rende juros de 9%. No ano
seguinte a ação pode aumentar 20% de valor, ou diminuir 10% ou permanecer alterada.
Estima-se que as probabilidades destas três ocorrências possíveis são de 0,3; 0,4 e 0,3
respectivamente. Que deveria ele fazer se só deseja investir durante um ano e os custos
de investimento forem os mesmos, nos dois casos? (10200; 10900-poupança)
山村
16
5.1
DISTRIBUIÇÃO BINOMIAL
Usa - se o termo binomial para designar situações em que os resultados de uma
variável aleatória podem ser agrupados em duas classes ou categorias. Os dados são nominais.
A distribuição binomial é uma distribuição discreta de probabilidade, aplicável sempre
que o processo de amostragem é do tipo do de Bernoulli; isto é:
a) Em cada tentativa existem dois resultados possíveis mutuamente exclusivos. Elas
são chamadas por conveniência, sucesso ou fracasso.
b) As séries de tentativas, ou observações são constituídas de eventos independentes.
c) As probabilidades de sucesso p, permanece constante de tentativa para tentativa
(estacionário).
Três valores são necessários:
X ⇒ número de sucessos, n ⇒ número de observações
p ⇒ probabilidade de sucesso em cada tentativa
P(X) =
( ). p
n
X
x
.q n − X =
n!
p X .q n − X
X !(n − X )!
Se for expressa por proporções:
X
X
n!
p =
⇒ P( p = ) =
p X q n− X
n
n
X !(n − X )!
E(X) = np
Var(X) = npq
Exercícios:
1) A probabilidade de que um presumível cliente aleatoriamente escolhido faça uma compra
é 0,20. Se um vendedor visita seis presumíveis clientes, qual a probabilidade de que fará
exatamente quatro vendas. (0,01536)
2) Idem, 4 ou mais vendas (0.01536+0.001536+0.000064=0.016960≅0.017)
3) Se a probabilidade de que um presumível cliente realize uma compra é 0,20, e se visita 15
presumíveis clientes, calcule o valor esperado do número de vendas e a variância (3,0:
2,4)
4) A probabilidade de que um empregado aleatoriamente escolhido participe de um
programa de investimento em ações proporcionado pela empresa é de 0,40. Se 5
empregados são escolhidos aleatoriamente, calcule a probabilidade de que a proporção de
participantes seja exatamente 0,60. (0,2304)
5) A probabilidade .....é de 0,40. Se 10 empregados são escolhidos aleatoriamente, calcule a
probabilidade de que a proporção dos participantes seja no mínimo 0,70.
(0.0425+0.0106+0.0016+0.0001=0.0548)
6) Devido às altas taxas de juros, uma firma informa que 30% de suas contas a receber de
outras firmas comerciais se encontram vencidas. Se um contador escolhe aleatoriamente
uma amostra de 5 contas, determinar a probabilidade de:
a) Nenhuma conta está vencida.
山村
17
b) Exatamente duas contas estão vencidas
c) A maioria das contas está vencida.
d) Exatamente 20% das contas estão vencidas. (0.16807-0.3087-0.16308-0.36015)
7) Uma empresa produz 10% de peças defeituosas. As peças são embaladas em caixas que
contém 12 peças. Calcule a probabilidade de um cliente comprar um caixa contendo:
a) Nenhuma peça defeituosa;
b) Uma peça defeituosa. (0,2824; 0,3766)
8) Um levantamento efetuado na carteira de uma agência bancária indicou que 20% dos
títulos eram pagos com atraso. Se em determinado dia foram pagos 20 títulos da carteira,
determine a probabilidade que:
a) No máximo dois sejam pagos com atraso,
b) No mínimo três sejam pagos sem atraso,
c) Mais de 70% sejam pagos sem atraso. (0,206; 1; 0,8050.)
9) Uma amostra de 15 peças é extraída, com reposição de um lote que contém 10% de peças
defeituosas. Calcule a probabilidade de que:
a) O lote não contenha peça defeituosa;
b) O lote contenha exatamente três peças defeituosas;
c) O lote contenha pelo menos uma peça defeituosa;
d) O lote contenha entre três e seis peças defeituosas;
e) O lote contenha de três a seis peças defeituosas.
(20,59; 12,9; 79,4; 5,3; 18,4)
10) Num hospital 5 pacientes devem submeter-se a uma cirurgia, da qual 80% sobrevivem.
Qual a probabilidade de que:
a) Todos sobrevivam,
b) Pelo menos dois sobrevivam,
c) No máximo 3 não consigam sobreviver. (0,3277; 0,9933.; 0,9933)
11) Um levantamento efetuado em um pregão da bolsa de valores mostrou que naquele dia
40% das empresas tiveram aumento do valor de suas ações, enquanto que as ações
restantes ficaram estáveis ou perderam valor. Um fundo negocia com ações de 10 destas
empresas. Calcule a probabilidade de que neste dia:
a) Todas as ações do fundo tenham se valorizado;
b) No máximo ações de duas empresas não tenham se valorizado;
c) Todas as ações do fundo tenham se desvalorizado ou ficaram estáveis.
(0,01; 1,23; 0,60)
12) Uma confecção de roupa infantil suspeita que 30% de sua produção apresenta algum
defeito. Se tal suspeita é correta, determine a probabilidade de que, numa amostra de
quatro peças. Sejam encontradas:
a) No mínimo duas peças com defeitos;
b) Menos que três peças boas. (34,83; 34,83.)
13) Uma empresa distribuidora costuma falhar em suas entregas de mercadorias 15% das
vezes, por atraso na entrega, mercadoria fora de especificação, danos etc., causando
reclamação por parte dos clientes. Calcule a probabilidade de:
a) Não ocorrer reclamação nas 10 entregas de hoje;
b) Acontecer pelo menos uma reclamação nas 10 entregas;
c) Acontecer no máximo uma reclamação nas 10 entregas.
(19,69; 47,8 ; 54,43.)
14) Sabe-se que 20% dos clientes vêm a agência bancária exclusivamente para fazer
depósitos. A agência, automatizando seus serviços, instalou caixas automáticas de
山村
18
depósitos, que deveriam ser utilizadas por estes clientes. Por falta de hábito, apenas 30%
destes clientes utilizam este serviço. Qual é a probabilidade de um funcionário,
consultando clientes em uma fila de nove indivíduos a espera de atendimento em caixas
comuns, encontrar pelo menos um cliente que deve ser instruído a usar o caixa automático
para depósito? (74,27.)
15) Os registros de uma pequena companhia indicam que 40% das faturas por ela emitidas são
pagas após o vencimento. De 14 faturas expedidas, determine a probabilidade de:
a)
Nenhuma ser paga com atraso,
b)
No máximo dois serem pagas com atraso,
c)
Ao menos 3 serem pagas com atraso (0,0008, 0,0398, 0,3075?).
16) Uma firma exploradora de petróleo acha que 5% dos poços que perfura acusam depósito
de gás natural. Se ela perfurar 6 poços, determine a probabilidade de ao menos um dar
resultado positivo. (0,2648)
17) Pesquisa médica indica que 20% da população em geral sofrem efeitos colaterais
negativos com o uso de uma nova droga. Se um médico receita o produto a 4 pacientes,
qual a probabilidade de:
a) Nenhum sofrer efeito colateral,
b) Todos sofrerem efeitos colaterais,
c) Ao menos um sofrer efeitos colaterais (0,4096, 0,0016, 0,5904)
18) Ao testar certo tipo de caminhão em um terreno acidentado, constatou-se que 20% dos
caminhões não conseguem terminar o teste sem ao menos um pneu furado. Qual a
probabilidade de que, dentre os próximos 10 caminhões a serem testados, de 5 a 8 tenham
um pneu furando? (0,033)
19) A probabilidade de um certo tipo de lâmpada queimar no período de 24 horas é de 0,01.
Qual a probabilidade de um luminoso com 10 dessas lâmpadas permanecerem totalmente
aceso durante aquele período? (0,904)
20) A probabilidade de um vendedor realizar uma venda com um único cliente é de 0,20. Ele
visita 30 clientes distintos. Qual a probabilidade de que:
a) Realize exatamente quatro vendas (0,1325),
b) Pelo menos 3 vendas. ((0,9558)
21) 41% dos estudantes praticam alguma atividade esportiva. Escolhem-se 6 ao acaso para
opinarem sobre esportes. Determine a probabilidade de:
a) Nenhum praticar esportes,
b) De todos praticarem esportes,
c) De ao menos a metade praticarem esportes. (0,042; 0,0048; 0,4766)
22) Um lote de 500 peças é aceita se uma amostra aleatória de 10 peças acusa menos de duas
defeituosas. O lote tem 5% de peças com defeito. Qual a probabilidade de ser aceita?
(0,9139)
23) Numa agência de viagens, de cada 100 passagens vendidas, 30 são para o Rio de Janeiro.
Na venda de seis passagens:
a) Qual a probabilidade de que quatro seja para o Rio de Janeiro?
b) Qual a probabilidade de que quatro ou mais sejam para o Rio de Janeiro?
c) Qual a probabilidade de que nenhuma seja para o Rio de Janeiro?
d) Qual a probabilidade de que no máximo duas sejam para o Rio de Janeiro?
R: 0,06; 0,07; 0,12 0,74
24) Supondo que uma empresa aérea ZZ detém 30% dos vôos domésticos, determine a
probabilidade de que, em oito acidentes aéreos, ocorram:
a) Cinco acidentes com aviões da empresa ZZ
山村
19
b) Menos de 3 acidentes com aviões da empresa ZZ
c) Nenhum acidente com aviões da empresa ZZ (0,047; 0,494; 0,058)
25) Após a realização de uma pesquisa, onde se obteve que 85% dos que reservam lugares
comparecem para o embarque, uma empresa aérea ZY passou a adotar a política de vender
105 passagens para um avião que dispõe de 98 assentos. Determine a probabilidade de
que:
a) Todos os assentos sejam preenchidos
b) Sobre um passageiro sem assento
c) Sobrem 3 assentos vazios (0,0039; 0,0018; 0,0333).
26) Seis parafusos são escolhidos aleatoriamente da produção de uma máquina que apresenta
10% de peças defeituosas. Qual a probabilidade de serem defeituosos:
a) Nenhum deles (0,53l4)
b) 2 deles (0,0984)
c) Pelo menos um parafuso (0,4686)
d) Todos os parafusos
27) Uma empresa produz parafusos dos quais 10% são defeituosos. Entre 4000 parafusos qual é a
média esperada de defeituosos? E o desvio padrão? (36;1,8)
28) Sabe-se que a procura semanal de certa peça sobressalente é em média de 0,15. Deseja-se saber
qual é a probabilidade, em uma determinada semana, serem demandadas:
a)
b)
c)
d)
Zero peças (0,8607)
1 peça (0,1291)
2 peças (0,0097)
Pelo menos 1 peça (0,1393).
29) Uma amostra de 15 peças é extraída, com reposição de um lote que contém 10% de peças
defeituosas. Calcule a probabilidade de que:
a) O lote não contenha peça defeituosa; (20,59).
b) O lote contenha exatamente três peças defeituosas; (12,9).
c) O lote contenha pelo menos uma peça defeituosa; (79,4).
d) O lote contenha entre três e seis peças defeituosas; (5,3).
e) O lote contenha de três a seis peças defeituosas. (18,4.).
30) Uma confecção de roupa infantil suspeita que 30% de sua produção apresenta algum
defeito. Se tal suspeita é correta, determine a probabilidade de que, numa amostra de
quatro peças. Sejam encontradas:
a) No mínimo duas peças com defeitos; (34,83).
b) Menos que três peças boas; (34,83)
31) Sabe-se que a probabilidade de um estudante que entra na Universidade se formar é 0,3;
Determine a probabilidade de que dentre 6 estudantes escolhidos aleatoriamente:
a) Nenhum se forme,
b) Pelo menos 2 se formem. (0,1176, 0,5798)
32) Se a probabilidade de ocorrência de uma peça defeituosa é 0,2, determine a média e o
desvio padrão da distribuição de peças defeituosas em um total de 600. (120, 9,8)
33) Seis parafusos são escolhidos aleatoriamente da produção de uma máquina que apresenta
10% de peças defeituosas. Qual a probabilidade de serem defeituosos: a) nenhum deles
(0,5314); b) dois deles (0,0984) c) pelo menos um parafuso (0,4686)
34) A companhia de aviação Golan afirma que 95% dos seus vôos chegam no horário. Se os
registros dos vôos dos últimos três meses forem retirados uma amostra aleatória de 10
vôos, pede-se calcular a probabilidade de que: a) pelo menos 8 vôos chegaram no horário
(98,85%); b) entre 7 e 9 vôos chegaram no horário (40,02%).
山村
20
35) A montadora de carros sabe que no transporte de carros entre a fábrica e a concessionária,
3% dos carros transportados sofrem alguma avaria na sua pintura. Se uma concessionária
receber 50 carros, pede-se calcular a probabilidade de que: a) nenhum dos carros
transportados sofra avaria na pintura (21,81%); b) dois ou mais carros sofram avaria na
pintura (44,47%).
36) Uma vendedora de automóveis descobriu, pela experiência, que duas entre dez pessoas
que são levadas para um test drive em um novo automóvel compra um carro. Suponha
que, em uma determinada noite, ela leve cinco pessoas para um test drive. Qual a
probabilidade de que ninguém, entre essas cinco pessoas, compre um carro? (0,3277).
山村
21
5.2
DISTRIBUIÇÃO DE POISSON
-
Distribuição discreta de probabilidades usada para determinar a probabilidade
de um dado número de sucessos quando os eventos ocorrem em um continuum
de tempo ou espaço.
A probabilidade de uma ocorrência é a mesma em todo o campo de observação
A probabilidade de mais de uma ocorrência em um único ponto é
aproximadamente zero
Número de ocorrências em qualquer intervalo é independente do número de
ocorrências em outros intervalos
-
Ex: defeitos por cm2, acidentes por dia, clientes por hora, chamadas telefônicas por
minuto, vacas por acre. Necessitamos somente de:
λ = número médio de sucessos para a específica dimensão de tempo ou espaço de
interesse.
λ X .e − λ
P(X/ λ ) =
X!
E(X) = λ
var(X) = λ
Exercícios
1. Um departamento de conserto de máquinas recebe uma média de 5 chamadas por hora.
Qual a probabilidade de que, em uma hora selecionada aleatoriamente, sejam recebidas
exatamente 3 chamadas. (0,l404)
2. Idem, menos do que 3 chamadas (0,0067+0,0337+0,0842 = 0,1246)
3. Na média, 12 pessoas por hora consultam um especialista em decoração de uma fábrica.
Qual a probabilidade de 3 pessoas consultarão o especialista durante um período de 10
minutos (0,1804)
4. Em média, seis pessoas por hora utilizam os serviços de caixa-automático de um banco
durante as horas de maior movimento em uma loja de departamentos. Qual a
probabilidade de:
a)
Exatamente 6 pessoas a usarão durante uma hora aleatoriamente escolhida.
(0,1606)
b)
Menos do que 5 pessoas durante uma hora aleatoriamente escolhida. (0,2851)
c)
Nenhuma pessoa usará num intervalo de 10 minutos (0,3679)
d)
Nenhuma pessoa usará num intervalo de 5 minutos (0,6065)
5. Suponha que o manuscrito de um livro texto tenha um total de 50 erros nas 500 páginas de
material. Se os erros estão distribuídos aleatoriamente ao longo do texto, determine a
probabilidade de que:
a)
Um capítulo cobrindo 30 páginas tenha dois ou mais erros (0,8008)
b)
50
(0,9596)
c)
Uma página aleatoriamente escolhida não tenha erro algum (0,9048)
6. A taxa de chegada de clientes em uma agência bancária é de quatro clientes por minuto.
Determine a probabilidade de chegarem mais que 14 clientes nos próximos dois minutos.
(1,72.)
山村
22
7. Em um pedágio de determinada rodovia chegam em média 600 carros por hora.
Determine a probabilidade de:
a)
Chegarem exatamente 10 carros em um minuto;
b)
Chegarem menos que cinco carros em um minuto;
c)
Chegarem pelo menos oito carros em 30 segundos.
(12,51; 2,93; 13,33.).
8. Suponha que os navios cheguem a um porto à razão de 2 navios por hora, e que essa razão
seja bem aproximada por processo de Poisson. Observando o processo durante um período
de meia hora, determine a probabilidade de:
a)
Não chegar nenhum navio,
b)
chegarem 3 navios (0,368, 0,061 µ = λt )
9. Num livro de 800 páginas há 800 erros de impressão. Qual a probabilidade de que uma
página contenha pelo menos 3 erros? (0,0803)
10. Numa estrada há 2 acidentes para cada 100 km. Qual a probabilidade de que em:
a) 250 km ocorram pelo menos 3 acidentes? (0,8753),
b) 300 km ocorram 5 acidentes? (0,1606)
11. A experiência mostra que de cada 400 lâmpadas, 2 se queimam ao serem ligadas. Qual a
probabilidade de que numa instalação de:
a) 600 lâmpadas, no mínimo 3 se queimem? (0,5768),
b) 900 lâmpadas, exatamente 8 se queimem? (0,0463)
12. Numa linha adutora de água, de 60 km de extensão, ocorrem 30 vazamentos no período de
um mês. Qual a probabilidade de ocorrer, durante o mês, pelo menos 3 vazamentos num
setor de 3 km de extensão? (0,1912)
13. Numa fita de som, há um defeito a cada 200 pés. Qual a probabilidade de que:
a) Em 500 pés não aconteça defeito? (0,0821),
b) Em 800 pés ocorram pelo menos 3 defeitos? (0,7619)
14. O número de mortes por afogamento em fins de semana, numa cidade praiana, é de 2 para
cada 50.000 habitantes. Qual a probabilidade de que em:
a) 200.000 habitantes ocorram 5 afogamentos? (0,0916),
b) 112.500 habitantes ocorram pelo menos 3 afogamentos? (0,8264)
15. Uma firma recebe 720 mensagens em seu fax em 8 horas de funcionamento. Qual a
probabilidade de que:
a) Em 6 minutos receba pelo menos 4 mensagens? (0,9788),
b) Em 4 minutos não receba mensagem alguma? (0,0025)
16. Em um pronto-socorro número de atendimentos de emergência tem uma média de 60
atendimentos por hora. Calcular a probabilidade de:
a) Não efetuar nenhum atendimento num intervalo de 5 minutos (0,00674),
b) Efetuar pelo menos 2 atendimentos num intervalo de 10 minutos (0,9995).
17. Na pintura de paredes aparecem defeitos em média na proporção de 1 defeito por m2.
Qual a probabilidade de aparecerem 3 defeitos numa parede de 2x2 m?(0,1952)
18. Os defeitos em rolos de tecido têm uma média de 2 defeitos por 10 metros. Compra-se
5m. Determine as probabilidades:
a)
Zero defeito;
b)
1 defeito;
c)
Mais de um defeito.
19. Em uma experiência de laboratório passam, em média, por contador, 4 partículas
radioativas por milissegundo. Qual a probabilidade de entrarem no contador 6 partículas
em determinado milissegundo? (0,1042)
山村
23
20. Um posto telefônico recebe, em média, 10 chamadas por minuto. Determine:
a) Não ocorrer nenhuma chamada em 1 minuto, e em dois minutos.(0,00004; 0).
b) Ocorrer menos que 3 chamadas em 2 minutos (0)
c) Ocorrer mais que 4 chamadas em 0,3 minutos. (0,1847)
21. Uma telefonista recebe em média 10 chamadas por minuto. Determine:
a)
Não ocorrer nenhuma chamada em 1 minuto, (0,000045).
b)
Ocorrer menos que 3 chamadas em 0,4 minuto, (0,2381).
c)
Ocorrer mais que 2 chamadas em 0,3 minuto, (0,5768).
d)
Ocorrer no máximo 4 chamadas em 0,2 minuto, (0,9473).
e)
Receber 3 ou mais chamadas em 0,7 minuto, (0,9704).
f)
Receber exatamente 2 chamadas em 0,3 minuto, (0,2240).
g)
Receber no mínimo uma chamada em 0,6 minuto, (0,9975).
h)
Receber até 2 chamadas em 0,5 minuto, (0,1246).
i)
Receber entre 7 e 9 chamadas em 0,8 minuto, (0,1396).
j)
Receber pelo menos 3 chamadas em 0,35 minuto.(0,6791)
22. Determinada loja vende em média 5 caixas de um artigo por dia. Determinar o número
mínimo de caixas que deva ter em estoque, de modo que não seja necessária a reposição
diária de estoque em mais que um dia por mês de 25 dias de trabalho. (9)
23. Sabe-se que a procura semanal de certa peça sobressalente é em média de 0,15. Deseja-se
saber qual é a probabilidade, em uma determinada semana, de serem demandadas: a) zero
peças (0,8607); b) 1 peça (12,91%); c) 2 peças (0,0097); d) 3 peças (0,0029); e) pelo
menos uma peça (0,1393)
24. Um industrial fabrica peças para a injeção eletrônica de automóveis com tal perfeição que
apenas 5 peças em mil apresentam defeitos. Após uma série de peças fabricadas examinase uma amostra aleatória de 800 peças. Deseja-se saber; a) qual a probabilidade de que
mais de 4 peças sejam defeituosas? (0,3710); b) qual a probabilidade de que menos de 2
sejam defeituosas? (0,0916); c) qual a probabilidade de que o número de peças defeituosas
seja exatamente 2? (0,1466)
25. O gerente do supermercado verificou que o erro de digitação cometido pelos caixas é de
0,35 por hora. Pede-se calcular a probabilidade de que um caixa cometa dois erros numa
hora. (0,04316)
山村
24
5.3
DISTRIBUIÇÃO NORMAL DE PROBABILIDADES
É uma distribuição de probabilidade contínua que é simétrica e mesocúrtica.
A curva que representa é freqüentemente descrita como tendo a forma de um sino.
Características do modelo:
Se uma variável aleatória x, com média µ e desvio padrão σ, apresenta as seguintes
características:
Valores da variável aleatória x mais próximos da média µ ocorrem com maior
freqüência;
Valores da variável aleatória x simétricos em relação à média ocorrem com
mesma freqüência; a região definida pelo gráfico da função e pelo eixo das
abscissas tem área unitária, então a variável aleatória x tem distribuição normal
de probabilidades. É importante na inferência estatística porque
As medidas produzidas em diversos processos aleatórios seguem esta
distribuição;
Probabilidades normais podem ser usadas freqüentemente como aproximações
de outras distribuições de probabilidade, tais como a distribuição binomial e a
de Poisson:
As distribuições de estatísticas de amostra tais como a média e a proporção
freqüentemente seguem a distribuição normal independentemente da
distribuição da população.
A função matemática que define este tipo de curva é:
f ( x) =
1
2πσ
−1 X − µ 2
(
)
e2
σ
Com x ε R
As tabelas de probabilidade normal são baseadas em uma distribuição particular: a
distribuição normal padronizada, com µ = 0 e σ = 1.
Qualquer conjunto de valores X normalmente distribuído pode ser convertido em
valores normais padronizados z pelo uso de :
z=
X −µ
σ
山村
25
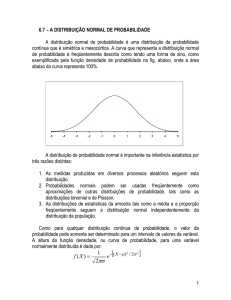
84,13%
15,87%
50%
34,13%
34,13% 15,87%
50%
100%
Exemplo
Os resultados de um teste feito com 200 alunos apresentou resultados normalmente
distribuídos com uma média de 60 e desvio padrão 8.
Cerca de 136 alunos (68%), encontrar-se-ão entre os 52 e os 68 pontos obtidos. Cerca
de 32 alunos (16%) terão resultados abaixo de 52 e cerca de 32 alunos terão resultados acima
de 68. Esta é uma das principais utilizações do desvio padrão e da distribuição normal.
A proporção relativa de números que, num conjunto de resultados, se situa entre os
desvios padrões é sempre a mesma. Temos sempre cerca de 68% dos resultados na faixa
compreendida entre um desvio padrão abaixo da média e um desvio padrão acima da média
(entre z = -1 e z= 1), independente dos valores reais dos resultados dos quais surge o desvio
padrão.
Os resultados padronizados só se aplicam a números obtidos com distribuições
normais.
Exercícios:
Se z tem distribuição normal padronizada, calcule:
1. a) P( z > 1,64 ) = (0,0505)
b) P( z < -l,64) = (0,0505)
c) P( 1 < z < 1,5) = (0,0919)
c) P( -1 < z < 2) = (0,8185)
d) P( -2 < z < 2) = (0,9544)
e) P(-1,64<z<-1,02) = (0,1034)
f ) P( z < 1,64) = (0,9495)
2. Se a variável é normal, calcule:
a) P(X > 6,8), se µ = 5 e σ = 3 = (0,2743)
b) P(X<800), se µ = 500 e σ = 200 = (0,9332)
c) P(9,9 <X<10,1), se µ = 10 e σ = 0,2 = (0,3830)
d) P(10<X<11), se µ = 10,73 e σ = 0,213 = (0,0062)
3. Determine os valores de z que correspondem às seguintes porcentagens:
a) área à esquerda de z = 0,0505 (-1,64)
b) área à esquerda de z = 0,0228 (-2)
c) área à direita de z = 0,0228 (2)
d) área entre 0 e z = 0,4772 (2)
e) área à esquerda de z =0,0107 (-2,3)
f) área entre z e –z = 0,9544 (2)
山村
26
DISTRIBUIÇÃO NORMAL
EXERCÍCIOS:
1. Sabe-se que a vida útil de um componente elétrico segue uma distribuição normal com
média µ = 2 000 horas e desvio padrão σ = 200 horas. Determine a probabilidade de que
um componente aleatoriamente escolhido dure:
a)
entre 2 000 e 2 400 horas (0,4772)
b)
dure mais que 2 200 horas ( 0,1587)
2. O processo de empacotamento em uma companhia de cereais foi ajustado de maneira que
uma média de µ = 13,0 kg de cereal é colocada em cada saco. Nem todos os sacos têm
precisamente 13,0 kg devido a fontes aleatórias de variabilidade. O desvio padrão do peso
líquido é σ = 0,1 kg, e sabe-se que a distribuição dos pesos segue uma distribuição
normal. Determine a probabilidade de que um saco aleatoriamente escolhido contenha :
a)
Entre 13,0 e 13,2 kg de cereal (0,4772)
b)
Entre 12,9 e 13,1 kg de cereal (0,6826)
c)
Entre 12,8 e 13,1 kg
(0,8185)
d)
Entre 13,1 e 13,2 kg
(0,1359)
3. O tempo necessário em uma oficina para o conserto da transmissão de um automóvel é
normalmente distribuído com µ = 45 minutos e σ = 8,0 minutos. O mecânico planeja
começar o conserto do carro do cliente 10 minutos após o carro ter sido deixado na
oficina, comunicando ao cliente que o carro estará pronto em uma hora. Qual a
probabilidade de que o mecânico esteja enganado? (0,2676)
a)
Qual a previsão de tempo de trabalho para que haja 90% de probabilidade de que
o conserto da transmissão se efetue dentro do tempo previsto? (55,24 min)
b)
Qual a previsão de tempo de trabalho para que haja uma probabilidade de 30% de
que o conserto seja efetuado dentro do tempo previsto? (40,84 min)
4. As notas de Estatística estão normalmente distribuídas com média 7,6 e desvio padrão 1,5
Sabe-se que 16,6% dos alunos que apresentaram as melhores notas receberam o grau A e
11,9% dos alunos menos adiantados receberam o grau B.
a) Determine o mínimo grau para receber A (9);
b) Determine a nota mínima para passar (5,8)
5. As vendas de determinado produto têm apresentado distribuição normal com média de
600 unidades/mês e desvio padrão 40 unidades/mês. Se a empresa decide fabricar 700
unidades naquele mesmo mês, qual é a probabilidade de não poder atender todos os
pedidos desse mês por estar com a produção completa? (0,0062)
6. Uma firma produz instrumentos de precisão cujos comprimentos têm distribuição
aproximadamente normal com µ = 78,3mm e σ = 1,4 mm. Se qualquer peça com mais de
80mm de comprimento deve ser rejeitado, qual a porcentagem da produção perdida?
(0,1131)
7. As notas de um teste de aptidão têm distribuição normal com média µ = 60 e desvio
padrão σ = 20. Que percentual das notas:
a)
Excede 85
(0,1056)
b)
Está abaixo de 50?
(0,3085)
8. O tempo necessário para completar uma tarefa escolar tem distribuição normal com média
de 90 minutos e desvio padrão de 15 minutos.
a)
Que porcentagem de estudantes terminará a tarefa em 2 horas?
山村
27
b)
Qual o tempo necessário para permitir que 90% dos estudantes terminem a tarefa?
(0,9772; 109 minutos).
9. Após 28 dias de curagem, o cimento PP comum tem resistência compressiva média 4000
psi e desvio padrão 120 psi. A resistência tem distribuição normal. Determine a
probabilidade para uma uma resistência compressiva de 28 dias:
a)
< 3900
(0,2033)
b)
< 3850
(0,1056)
c)
> 3850
(0,8944)
d)
> 3880
(0,8413)
10. A renda média de uma grande comunidade é razoavelmente aproximada por uma
distribuição normal com média $ 15 000 e desvio padrão $ 3 000.
a) Que percentagem da população terá renda superior a $ 18 600? (0,1151)
b) Numa amostra de 50 assalariados, quantos podemos esperar que tenham menos de $
10 500 de renda? (3,34)
11. Uma distribuição normal têm média 50 e desvio padrão 5. Que percentagem da população
está em cada um dos intervalos:
a) De 40 a 50
(0,4772)
b) De 49 a 50
(0,0793)
c) De 40 a 45
(0,1359)
d) De 56 a 60
(0,0923)
e) De 40 a 65
(0,9758)
f) De 45 a 55
( 0,6826)
12. Em um grande complexo industrial, o departamento de manutenção tem instruções para
substituir as lâmpadas antes que se queimem (não esperar que queimem para então
substituí-las). Os registros indicam que a duração das lâmpadas tem distribuição normal
com média 900 horas e desvio padrão 75 horas. Quando devem ser substituídas as
lâmpadas de modo que no máximo 10% delas queimem antes de serem trocadas? (dentro
de 804 horas )
13. A vida média útil de certo utensílio é de 1,5 ano, com desvio padrão de 0,3 ano. Se os
defeitos se distribuem normalmente, que percentagem dos aparelhos vendidos necessitará
de reparo antes de expirar a garantia de um ano? (4,75%)
14. Os registros indicam que o tempo médio para se fazer um teste é aproximadamente
normal com média 80 minutos e desvio padrão de 20 minutos. Determinar:
a) Porcentagem de candidatos que levam menos de 80 minutos,
b) Se o tempo médio concedido é de 1h45min. Que percentagem não conseguirá
terminar o teste?
c) Se 150 pessoas se submetem ao teste, quantas podemos esperar que terminem o
teste dentro de 1 hora? (50%, 10,56%, 24)
15. O levantamento do custo unitário de produção de um item da empresa revelou que sua
distribuição é normal com média 50 e desvio padrão 4. Se o preço de venda unitário desse
produto é 60, qual a probabilidade de uma unidade desse item escolhida ao acaso
ocasionar prejuízo a empresa? (0,621)
16. Uma empresa produz um equipamento cuja vida útil admite distribuição normal com
média 300 h e desvio padrão 20h. Se a empresa garantiu uma vida útil de pelo menos
280h para uma das unidades vendidas, qual a probabilidade de ela ter que repor essa
unidade? (15,866)
山村
28
17. Os balancetes semanais realizados em um empresa mostraram que o lucro realizado
distribui-se normalmente com média 48.000 u. m. e desvio padrão 8.000 u. m. Qual a
probabilidade de que:
a)
Na próxima semana o lucro seja maior que 50.000 u.m.?,
b)
Na próxima semana o lucro esteja entre 40.000 u. m. e 45.000 u.m.?,
c)
Na próxima semana haja prejuízo? (40,129; 19,33; 0%)
18. O departamento de marketing da empresa resolve premiar 5% dos seus vendedores mais
eficientes. Um levantamento das vendas individuais por semana mostrou que elas se
distribuíam normalmente com média 240.000 u.m. e desvio padrão 30.000 u.m. Qual o
volume de vendas mínimo que um vendedor deve realizar para ser
premiado?(289.200,00).
19. Uma máquina produz um tubo de plástico rígido cujo diâmetro admite distribuição normal
de probabilidades, com média 100mm e desvio padrão 0,5 mm. Os tubos com diâmetro
menor que 98,2mm ou maior que 100,6mm são considerados defeituosos, e devem ser
reciclados. Qual a proporção da produção que deverá ser reciclada? (11,523.)
20. Os salários dos funcionários de um hotel fazenda têm distribuição normal em torno da
média de $ 1.500,00, com desvio padrão de $ 200,00. Qual a probabilidade de um
funcionário:
a)
Ganhar entre $ 1000,00 e $ 1 600,00?
b)
Ganhar acima de $ 1 500,00?
c)
Ganhar acima de $ 1 400,00?
d)
Ganhar abaixo de $ 1 400,00?
e)
Ganhar acima de $ 1 650,00? (0,383; 0,0,5; 0,6915; 0,3085; 0,2266)
21. Os pesos de 500 malas são normalmente distribuídos com média 66,2 kg e desvio padrão
de 4,3 kg. Determine o número de malas que pesam:
a) Menos que 66,2 kg
b) Entre 63 e 68 kg
c) Menos de 70 kg
d) Mais de 60 kg (250, 217, 405, 463).
22. Um avião de oito lugares executa vôos turísticos ecológicos de uma cidade para uma ilha.
O avião pode levar carga útil de 650 kg. Supondo que os passageiros têm peso médio de
600 kg e desvio padrão de 80 kg, e que o peso é normalmente distribuído, qual a
probabilidade de:
a) O peso dos oito passageiros estar entre 550 e 680 kg?
b) Haver sobrecarga se o piloto não pesar os oito passageiros?
c) Que o piloto tenha de tirar menos de 50 kg de gasolina para evitar sobrecarga?
(0,8112; P(X>650=0,2676; 650<P(X)< 700=0,162)
23. As alturas dos jovens de um acampamento são normalmente distribuídas com média de
1,70 m e desvio padrão de 0,30 m. Os jovens deverão participar de diversas atividades
esportivas. Para estabelecer as equipes, encontre a probabilidade de um jovem medir:
a) Entre 1,58 e 1,85m
b) Mais de 1,75 m
c) Menos de 1,60m
d) Mais de 1,90 m (0,3469; 0,4325; 0,3707; 0,2514)
24. Sabe-se que uma variável aleatória normalmente distribuída tem por média 88,5 e por
desvio padrão 6,4. Determinar a probabilidade dessa variável situar-se:
a) No intervalo entre 88,5 e 98 (0,4306)
b) No intervalo entre 80 e 98 (0,4082)
山村
29
c)
d)
e)
f)
g)
h)
No intervalo entre 94,5 e 100 (0,1407)
No intervalo entre 94,5 ou mais (0,1736)
Acima de 95 (0,1379)
Abaixo de 90 (0,5636)
Classifique em percentis os que conseguiram 85; 88,5; 98 e 100 (93; 97).
Para se conseguir classificação no percentil 99, qual será o número de pontos
necessários(113,4)
25. Uma empresa usa anualmente milhares de lâmpadas elétricas, que permanecem acesas
continuamente, dia e noite. A vida de uma lâmpada pode ser considerada uma v. a.
normal, com média de 50 dias e d. p. de 15 dias. Em 1o de janeiro a companhia instalou 8
000 lâmpadas novas. Aproximadamente quantas deverão ser substituídas até 1o de
fevereiro?(0,0918, 734)
26. Os depósitos mensais na caderneta de poupança têm distribuição normal com média igual
a $ 500 e desvio padrão $ 150. Se um depositante realizar um depósito, pede-se calcular a
probabilidade de que esse depósito seja: a) igual ou menor que $ 650 (84,13%) b) igual ou
maior que 650 (15,87%); c) seja um valor entre $250 e $650 (79,36%)
27. As vendas mensais dos últimos 50 meses apresenta uma média de $ 500 mil com desvio
padrão igual a $ 80 mil. Se a empresa estabeleceu uma meta de vendas para o próximo
mês de $ 550 mil, pede-se calcular, considerando que os dados históricos se repetem no
futuro: a) a probabilidade de ficar abaixo da meta (73,40%); b) a probabilidade de superar
a meta (26,60%) c) a probabilidade de que as vendas se situem entre 80% e 110% da
média (62,84%)
28. Dado que uma população com média 25 e desvio padrão 2 tem distribuição normal,
determine os valores de z para os seguintes valores da população :
a) 23,0 (-1) b) 23,5 (-0,75) c) 24,0 (-0,5) d) 25,2 (0,1)
Uma população normal tem média 40 e desvio padrão 3. Determine os valores
correspondentes aos seguintes valores de z:
a) 0,10 (40,3) b) 2,00 (46) c) 0,75 (42,25) d) -2,53 (32,41)
山村
30
EXERCÍCIOS GERAIS
1. Uma moeda não viciada é lançada 8 vezes. Encontre a probabilidade de:
a)
dar 5 caras;
(0,22)
b)
pelo menos uma cara;
(0,996)
c)
no máximo duas caras;
(0,14)
d)
calcular a média e o desvio padrão (4;
2 ) n= 8, p=0,5, q=0,5)
2. Em média há 2 chamadas por hora num certo telefone. Calcular a probabilidade de se
receber no máximo 3 chamadas em duas horas e a probabilidade de nenhuma chamada em
90 minutos.(0,0183, 0,0732, 0,1464, 0,1952=0,4332; 0,0498)
3. Admitindo-se que os nascimentos de meninos e meninas sejam iguais, calcular a
probabilidade de um casal com 6 filhos ter 4 filhos homens e 2 mulheres.(15/64)
4. Em 320 famílias com 4 crianças cada uma, quantas se esperaria que tivessem:
a)
nenhuma menina;
b)
3 meninos;
c)
4 meninos (20, 80. 20)
5. Um time X tem 2/3 de probabilidade de vitória sempre que joga. Se X jogar 5 partidas,
calcule a probabilidade de:
a)
vencer exatamente 3 partidas;
b)
vencer ao menos uma partida;
c)
vencer mais da metade das partidas. (80/243; 242/243;64/81)
6. A probabilidade de um atirador acertar o alvo é 1/3. Se ele atirar 6 vezes, qual a
probabilidade de:
a)
acertar exatamente 2 tiros;
b)
não acertar nenhum tiro.(80/243; 64/739)
7. Uma fábrica de pneus verificou que ao testar seus pneus nas pistas, havia em média um
estouro de pneu a cada 5 000 km.
a)
qual a probabilidade que num teste de 3 000 km haja no máximo um pneu
estourado;
b)
qual a probabilidade de que um carro ande 8 000 km sem estourar nenhum pneu
(0,8784;0,2020)
8. Certo posto de bombeiros recebe em média 3 chamadas por dia. Calcular a probabilidade
de:
a)
receber 4 chamadas num dia;
b)
receber 3 ou mais chamadas num dia (0,168; 0,5767)
9. A média de chamadas telefônicas em uma hora é 3. Qual a probabilidade de:
a)
receber exatamente 3 chamadas numa hora;
b)
receber 4 ou mais chamadas em 90 minutos.(0,2241;0,658)
10. Suponha que haja uma média de 2 acidentes de trabalho graves por ano numa população
de 50 000. Em uma cidade de 100 000 habitantes, encontre a probabilidade de que em
dado ano tenha havido:
a)
0,
b)
l,
c)
2,
d)
2 ou mais acidentes graves.(0,0183, 0,0732, 0,1464, 0,9085)
11. Suponha 400 erros de impressão distribuídos aleatoriamente em um livro de 500 páginas.
Encontre a probabilidade de que uma dada página contenha:
a)
nenhum erro,
山村
31
b)
exatamente 2 erros. (0,449; 0,1437)
12. Uma loja atende em média 2 clientes por hora. Calcular a probabilidade de em uma hora:
a)
atender exatamente 2 clientes,
b)
atender 3 clientes. (0,270; 0,180)
13. A duração de um certo componente eletrônico tem média 850 dias e desvio padrão 45
dias. Calcule a probabilidade desse componente durar:
a)
entre 700 e 1 000 dias,
b)
mais que 800 dias,
c)
menos que 750 dias,
d)
exatamente 1 000 dias.
e)
Qual deve ser o número de dias necessários para que tenhamos de repor no
máximo 5% dos componentes ?(1, 0.8665,0.0132, 0, 776 dias)
14. Os pesos de 600 estudantes são normalmente distribuídos com média 65,3 kg e desvio
padrão de 5,5 kg. Encontre o número de alunos que pesam:
a)
entre 60 e 70 kg,
b)
mais que 63,2 kg (380, 389)
15. Suponha que as notas de uma prova sejam normalmente distribuídos com média 73 e
desvio padrão 15. 15% dos alunos mais adiantados recebem a nota A e 12% dos mais
atrasados recebem a nota F. Encontre o mínimo para receber A e o mínimo para passar,
não receber F (88.6, 55)
16. Uma fábrica de pneus fez um teste para medir o desgaste de seus pneus e verificou que ele
obedecia a uma distribuição normal, de média 48 000 km e desvio padrão 2 000 km.
Calcule a probabilidade de um pneu escolhido ao acaso:
a)
durar mais que 46 000 km,
b)
dure entre 45 000 e 50 000 km. (0.8413, 0.7745)
17. Em uma distribuição normal, 28% dos elementos são superiores a 34 e 12% inferiores a
19. Encontrar a média e a variância da distribuição. (29.03, 73.44)
18. A altura dos homens americanos segue uma distribuição aproximadamente normal com
média µ = 69 polegadas e desvio padrão σ = 3 polegadas. Qual a probabilidade de um
homem selecionado aleatoriamente Ter altura superior a 75 polegadas? ( 0,0228 )
19. Uma firma produz ferrolhos cujos comprimentos têm distribuição normal com µ= 78,3
mm e σ = 1,4 mm. Se qualquer ferrolho com mais de 80 mm de comprimento deve ser
rejeitado, qual a proporção da produção perdida? (0,1131)
20. As notas de um teste de aptidão tem distribuição normal com média µ = 60 e desvio
padrão σ = 20. Que proporção das notas
a) excede 85 (0,1056)
b) está abaixo de 50; (0,3085)
21. Os resultados de um exame nacional para estudantes recém formados apresentaram uma média µ
= 500 com desvio padrão σ = 100. Os resultados têm uma distribuição aproximadamente normal.
Qual a probabilidade de que o grau de um indivíduo escolhido aleatoriamente esteja:
a) entre 500 e 650 (0,4332)
b) entre 450 e 600 (0,5328)
c) inferior a 300 (0,0228)
d) superior a 650 (0,0668)
22. A vida útil de uma certa máquina de pneus radiais tem uma distribuição normal com µ= 38.000
km e σ= 3.000 km. Qual a probabilidade de um pneu escolhido aleatoriamente tenha uma vida útil
de:
a) no mínimo 35 000 (0,8413)
b) mais do que 45 000 (0,0099)
山村
32
23. Um comerciante encomenda 500 dos pneus acima descritos para revendê-los. Qual a quantidade
aproximada de pneus que terá uma vida:
a) entre 40 000 e 45 000 km (121)
b) 40 000 km ou mais (126)
24. Segundo as condições específicas do ex 6,dentro de que período de tempo os 20% de
pessoas que realizam as transações mais rápidas terminam seus negócios no guichê.(92 s)
25. Em uma distribuição normal, 29,12% dos elementos são superiores a 38 e 12,71%
inferiores a 23. Encontrar a média e a variância da distribuição. (33,l; 8,9)
山村
33
5.4
APROXIMAÇÃO PELA NORMAL DAS PROBABILIDADES BINOMIAIS
Sempre que n ≥ 30, e tanto np ≥ 5 como nq ≥ 5
A média e o desvio padrão se baseiam em µ = np
σ = npq
APROXIMAÇÃO PELA NORMAL DAS PROBABILIDADES DE POISSON
Sempre que λ ≥ 10
A média e o desvio padrão da distribuição normal de probabilidades baseiam se em
µ =λ
e
σ= λ
CORREÇÃO DE CONTINUIDADE
a)
b)
c)
d)
Subtrair 0.5 de X quando é solicitada P(X ≥ Xi )
Subtrair 0.5 de X quando é solicitada P(X < Xi )
Adicionar 0.5 de X quando é solicitada P(X ≤ Xi)
Adicionar 0.5 de X quando é solicitada P(X > Xi)
Exercícios:
1. Para um grande número de clientes potenciais, sabe-se que 20% dos contatados
pessoalmente por agentes de vendas realizarão uma compra. Se um representante visita 30
clientes potenciais, determine a probabilidade de que 10 ou mais farão a compra. (0,0548)
2. Um departamento de consertos de máquinas recebe, em média, 10 chamadas em cada
período de 8 horas. Determine a probabilidade de que mais do que 15 chamadas serão
recebidas em um período de 8 horas aleatoriamente escolhido. (0,0409)
3. Sabe-se que 70% das pessoas que entram em um centro comercial realizam pelo menos
uma compra. Para uma amostra de n = 50 pessoas, qual a probabilidade de que no mínimo
40 pessoas façam, cada uma, uma ou mais compras? (0,0823)
4. Qual a probabilidade, de que menos que 30 das 50 pessoas amostradas realizem pelo
menos uma compra, referida ao ex 3? (0,0446)
5. Sabe-se que os pedidos de serviço chegam aleatoriamente numa média de 5 por hora. Qual
a probabilidade de que sejam recebidas mais de 50 pedidos em um período de 8 horas?
(0,0485)
6. Qual a probabilidade de que cheguem 35 pedidos ou menos durante um período de 8
horas, referida ao ex.5? (0,2388)
7. A proporção de motores defeituosos numa linha de montagem é 0,10 e uma amostra de
200 motores é incluída em um carregamento particular. Qual a probabilidade de que pelo
menos 30 dos 200 motores sejam defeituosos? (0,0125)
8. Em média 0,5 clientes por minuto chegam a um balcão. Qual a probabilidade de que em
um intervalo de meia hora, cheguem ao balcão mais do que 20 clientes? (0,0778)
9. Um sistema é formado por 100 componentes, cada um dos quais com confiabilidade de
0,95 (probabilidade de funcionamento do componente durante um certo período de
山村
34
tempo). Se esses componentes funcionam independentemente um do outro e se o sistema
completo funciona adequadamente quando pelo menos 80 componentes funcionam, qual a
confiabilidade do sistema? (0,9941)
10. Os resultados de um exame nacional para estudantes recém formados apresentaram uma
média µ = 500 com desvio padrão σ = 100. Os resultados têm uma distribuição
aproximadamente normal. Qual a probabilidade de que o grau de um indivíduo escolhido
aleatoriamente esteja:
a)
entre 500 e 650
(0,4332),
b)
entre 450 e 600
(0,5328),
c)
inferior a 300
(0,0228),
d)
superior a 650
(0,0668)
11. A vida útil de uma certa máquina de pneus radiais tem uma distribuição normal com µ =
38.000 km e σ = 3.000 km. Qual a probabilidade de um pneu escolhido aleatoriamente
tenha uma vida útil de:
a)
no mínimo 35.000
(0,8413)
b)
mais do que 45.000
(0,0099)
12. Um comerciante encomenda 500 dos pneus acima descritos para revendê-los. Qual a
quantidade aproximada de pneus que terá uma vida:
a)
entre 40.000 e 45.000 km (121)
b)
40.000 km ou mais (126)
13. O tempo necessário para o atendimento de uma pessoa em um guichê de um banco tem
distribuição aproximadamente normal com µ = 130 s e σ = 45 s. Qual a probabilidade de
que um indivíduo aleatoriamente selecionado:
a)
requeira menos que 100 segundos para terminar suas transações (0,2514)
b)
gaste entre 2 e 3 minutos no guichê (0,4536)
14. Segundo as condições específicas do ex 6,
a)
dentro de que período de tempo os 20% de pessoas que realizam as transações
mais rápidas terminam seus negócios no guichê.(92 s),
b)
Qual é o tempo mínimo necessário para os 5% de indivíduos com as transações
mais complicadas (204 s)
15. Para os vários milhares de artigos estocados por uma firma que atende encomendas
postais, há uma probabilidade de 0,08 de que um artigo em particular (incluindo
especificações de tamanho e cor) esteja esgotado. Se uma encomenda engloba pedidos de
120 itens diferentes, qual a probabilidade de que:
a)
15 ou mais artigos estejam esgotados? (0,0495),
b)
estarem esgotados entre 10 e 15 artigos inclusives? (0,4887)
16. Entre as 16 e as 18 horas, período de maior movimento em um posto de gasolina, entra no
posto, em média, um carro a cada 3 minutos.
a)
Qual a probabilidade de que pelo menos 25 automóveis entrem no posto entre as
16 e 17 horas? (0,1562),
b)
menos do que 30 automóveis entrem no posto entre as 16 e 18 horas de um dia
aleatoriamente escolhido (0,0485)
17. A proporção de motores defeituosos numa linha de montagem é 0,10 e uma amostra de
200 motores é incluída em um carregamento particular. Qual a probabilidade de que pelo
menos 30 dos 200 motores sejam defeituosos? (0,0125)
18. Em média 0,5 clientes por minuto chegam a um balcão. Qual a probabilidade de que em um
intervalo de meia hora, cheguem ao balcão mais do que 20 clientes? (0,0778)
山村
35
19. Atualmente, cerca de dois terços das companhias americanas fazem teste do uso de drogas em
empregados recém-admitidos, e os resultados do teste em 3,8% dos empregados dão positivo (com
base em dados da American Management Association). Uma companhia testa 150 candidatos a
emprego e constata que, em 10 deles, o teste foi positivo. Estime a probabilidade de 10 ou mais
resultados positivos em 150 candidatos. Com base nesse valor, os 10 resultados parecem uma cifra
elevada? (0,0526, não)
20. Um hospital necessita de 177 doadores de sangue do grupo O. Se 400 voluntários doam sangue,
estime a probabilidade de haja pelo menos 177 com sangue desse grupo, sabendo-se que quarenta
e cinco por cento da população de onde vieram esses voluntários têm sangue do grupo O. (0,6368)
山村
36
6
INFERÊNCIA ESTATÍSTICA ( analítica) : Distribuição de Amostragem
A inferência estatística é o processo que consiste em utilizar informações colhidas da
observação de uma amostra, para estimar características da população da qual se extraiu a
amostra. Uma estatística é um valor calculado com base em valores observados de uma
amostra. A estimação é um processo que consiste em avaliar os parâmetros de uma
distribuição através dos estimadores obtidos em uma amostra, com base no cálculo de
probabilidades. Um estimador é uma estatística utilizada para estimar o valor de uma
grandeza desconhecida de uma população. A qualidade de uma estimação depende
basicamente da representatividade da amostra(consiste na capacidade de reproduzir as
características importantes da população)
DIMENSIONAMENTO DA AMOSTRA
Procedimento:
1. Analise o questionário, ou roteiro da entrevista e escolha a(s) variável(eis) que julgue mais
importante para o estudo.
2. Verifique o nível de mensuração da variável: se nominal, ordinal ou intervalar.
3. Considere o tamanho da população: infinita ou finita.
4. Determine o tamanho da amostra (n), se a variável for intervalar e a população for
considerada infinita, por: z = abscissa da curva normal padrão, fixado um nível de
confiança z = 2, se o nível for 95,5%
 zσ 
n =

 d 
2
z = 1,96
se o nível for 95%
z = 2,57 se o nível for 99%.
σ = desvio padrão da população, expresso na unidade variável,
Usualmente z = 2
determinado por: especificações técnicas, ou referendando o valor de estudos semelhantes, ou
fazendo conjeturas sobre possíveis valores.
d = erro amostral, expresso na unidade da variável. É a máxima diferença que o investigador
admite suportar entre a µ (desconhecido) e X (média amostral).
1.
2.
VARIÁVEL INTERVALAR E POPULAÇÃO FINITA
z 2σ 2 N
n= 2
N = tamanho da população
d ( N − 1) + z 2σ 2
Um estudo do peso de certa peça retirado de uma população infinita, tem σ =
10 kg. Admitindo-se um nível de confiança de 95,5% e um erro amostral de
1,5 kg, determinar o tamanho da amostra. (178)
Admita os mesmos dados e que a população seja finita de 600 peças. (138)
COMPOSIÇÃO DA AMOSTRA
1. Métodos probabilísticos: amostragem aleatória simples, amostragem sistemática,
amostragem estratificada, amostragem por conglomerados (agrupamentos)
2. Método intencional: amostragem acidental, intencional, por quotas.
山村
37
ESTIMAÇÃO POR PONTO
Por causa de fatores como tempo e custo, os parâmetros de uma população são
freqüentemente estimados com base em estatísticas de amostra.
Por outras palavras, estimador é a quantidade, calculada em função dos elementos da
amostra, que será utilizada no processo de estimação do parâmetro desejado.
Estimadores por ponto freqüentemente utilizados
Parâmetro populacional
Estimador
Média, µ
Diferença entre duas médias, µ1-µ2
Proporção, π
Diferença entre duas proporções, π1-π2
Desvio padrão, σ
X
X1 − X 2
p
p1 − p 2
s * (correção
incluída)
Se não estiver incluída, o estimador apropriado seria
de
continuidade
s
n
n −1
As qualidades que deve ter um estimador θ são:
a) Consistência (a distribuição da média amostral se concentra em torno da média da
população quando a amostra é suficientemente grande), ausência de vício, não
tendencioso ou não-viesado,
∧
E (θ ) = θ
b) Eficiência (para um mesmo tamanho de amostra um parâmetro é mais eficiente em
relação a outro quando sua variância é menor que a do outro) e,
c) suficiência ( quando contém o máximo possível de informações com relação ao
parâmetro estimado).
Critérios para a escolha dos estimadores
A adequação se dá nos métodos da máxima verossimilhança, dos momentos e de
Bayes, dentre outros.
O método da máxima verossimilhança tem sido o mais empregado, fornece em geral
estimadores consistentes, assintoticamente eficientes e com distribuição assintoticamente
normal. A essência do método consiste em adotar para o parâmetro o valor que maximize a
função de verossimilhança correspondente ao resultado obtido na amostra (Costa Neto, 1977,
p. 62).
O método dos momentos consiste em supor que os momentos da distribuição da
população coincidem com os da amostra. Expressando os parâmetros populacionais a estimar
em função dos momentos de menor ordem, obtém-se um sistema de equações cuja solução
fornece as estimativas desejadas, produz, em geral estimadores consistentes, mas que, muitas
vezes, não são os mais eficientes.
O método de Bayes baseia-se na existência de uma função de perda associada ao erro
da estimativa, e também na consideração de uma distribuição a priori para os possíveis
valores do parâmetro. É adotada a estimativa que minimize o valor médio ou expectância da
山村
38
perda, calculada com base na distribuição resultante para o parâmetro após o conhecimento
dos valores da amostra. A essência do método considera uma função de perda associada à
estimativa e admite uma especificação do modelo de distribuição do parâmetro que pode ser
afetada até certo ponto pela evidência amostral.
山村
39
7
DISTRIBUIÇÃO DE AMOSTRAGEM DA MÉDIA
Distribuição de probabilidade para os possíveis valores da média da amostra X
baseados em um particular tamanho da amostra. Para qualquer "n" amostral de uma
população com média µ, o valor da média X irá variar de amostra para amostra. Esta
variabilidade serve como base da distribuição de amostragem. A distribuição de amostragem
da média é descrita pela determinação do valor esperado E( X ) e do desvio padrão da
distribuição das médias σ X (erro padrão da média). Em geral são definidos como:
n ≥ 30
σX=
E( X )= µ
PARA POPULAÇÃO FINITA
σX
σ
n
se n > 0,05 N ⇒ fator de correção finita
σ N −n
=
n N −1
Se o desvio padrão da população for desconhecido, o erro padrão da média pode ser
estimado, usando-se, o desvio padrão amostral como um estimador do desvio padrão da
população ( σ X ⇒ s X )
sX =
s
n
e
sX =
s
n
N −n
N −1
EXERCÍCIOS:
1. A média de uma população bastante grande é µ = 50,0 e o desvio padrão σ=12,0.
Determine a distribuição de amostragem das médias das amostras de tamanho n = 36 em
termos de valor esperado e de erro padrão da distribuição. (50,0; 2,0)
2. Um auditor toma amostras aleatórias de tamanho n = 16 de um conjunto de N= 100 contas
a receber. Não se conhece o desvio padrão das 100 contas a receber. Contudo o desvio
padrão da amostra é s = $ 57,00. Determine o valor do erro padrão da distribuição da
amostragem da média. (13.13)
3. Um auditor toma uma amostra de n = 35 de uma população de 1000 contas a receber. O
desvio padrão da população é desconhecido, mas o desvio padrão da amostra é s =$43,00.
Se o verdadeiro valor da média da população de contas a receber é µ = $ 260,00, qual a
probabilidade de que a média da amostra seja menor ou igual a $ 250,00?(0,0823)
4. Um analista do departamento de pessoal deseja estimar o número médio de horas de
treinamento anual para os funcionários de uma divisão da companhia, com um fator de
erro de 3,0 horas (para mais ou menos) e com 90% de confiança. Baseado em dados de
outras divisões, ele estima o desvio padrão das horas de treinamento em σ = 20,0 horas.
Determine o tamanho mínimo da amostra. (121)
5. A vida útil de operação de um tubo de imagem para TV de certa marca é, em média, µ = 9
000 horas com um desvio padrão de σ = 500 horas. Determine o valor esperado e o erro
山村
40
6.
7.
8.
9.
padrão da distribuição de amostragem para a média, sendo o tamanho da amostra n = 25.
(9.000; 100)
Um analista financeiro toma uma amostra aleatória de 10% de 300 contas e acha que o
saldo médio das contas é X = 148,50 com um desvio padrão de s= 35,75. Qual o valor
estimado do erro padrão da média? (6,20)
Do exerc. 6, se a média das contas é µ = $ 138,00. Qual a probabilidade de se obter uma
média de amostra igual ou superior a $ 148,50? (0,0455)
Uma população consiste apenas dos seguintes valores: 3, 5, 7, 8. Calcule: a) média da
população (µ = 5,75)
b) o desvio padrão da população( σ = 1,92)
Do exerc. 8 sorteie amostras aleatórias simples de tamanho n = 2 onde para cada amostra
o primeiro item sorteado não é reposto na população antes de se sortear o segundo.
a) liste todos os possíveis pares
b) para cada um dos pares identificados em (a) calcule a média da amostra X , e
compare com a média de todas as possíveis médias amostrais, µ X , é igual a média da
população da qual foi extraída a amostra.
c) Calcule o erro padrão da média.
10. Após o Plano Real, o gerente da agência bancária verificou que o saldo médio das contas
correntes aumentou. Considerando todos os clientes da agência, a média e o desvio padrão
do saldo médio das contas correntes são respectivamente $ 325 e$ 114. Se for retirada
uma amostra aleatória de 100 contas correntes, pede-se determinar a probabilidade que a
média dos saldos médios seja: a) menor que $ 330 (66,95%), b) maior que $ 350 (1,42%)
11. A garrafa de vinho branco importado é vendida na maior parte dos supermercados do país.
Levantamentos realizados pelo distribuidor desse vinho em todos os pontos de vendas
mostraram que a média do preço de venda ´$6,35 com desvio padrão igual a $ 1,90. Se for
retirada uma amostra aleatória em 45 pontos de vendas, pede-se determinar a
probabilidade que a média do preço de venda da garrafa de vinho, seja: a) menor que $ 6
(10,83%); b) maior que $7 (1,09%)
山村
41
8
INTERVALOS DE CONFIANÇA PARA A MÉDIA
Um intervalo de confiança para a média é um intervalo estimado, construído com
respeito à média da amostra, pelo qual pode ser especificada a probabilidade do intervalo
incluir a média da população. O grau de confiança associado com o intervalo de confiança
indica a porcentagem de tais intervalos que incluiriam o parâmetro que está sendo estimado.
População
Normalmente
Distribuída
Não normalmente
Distribuída
Estimação por intervalo da média da população
Tamanho
da σ conhecido
σ desconhecido
amostra
n ≥ 30
X ± zσ
X ± zs
X
X
n < 30
X ± zσ X
X ± ts X
n ≥ 30
X ± zσ X
X ± zs X
X ± kσ X
X ± ks X
2
onde 1 -- 1/k é definido onde 1 -- 1/k2 é definido
usando-se
a usando-se
a
desigualdade
de desigualdade
Chebyshev
de Chebyshev
Os intervalos de confiança mais utilizados são os de 90%, 95% e 99%. Os valores de
z requeridos para tais intervalos são respectivamente: 1,65; 1,96; 2,58.
n< 30
1.
2.
3.
4.
EXERCÍCIOS:
Para uma dada semana, foi tomada uma amostra aleatória de 30 empregados selecionados
de um grande número de empregados de uma fábrica, a qual apresentou um salário médio
de X = $ 180,00 com um desvio padrão da amostra de s = $ 14,00. Estime o salário médio
para todos os empregados da fábrica com uma confiança de 95% de que o intervalo inclua
a média da população. (174,96 a 185,02)
A vida média de operação para uma amostra de n = 10 lâmpadas é X = 4.000 horas com o
desvio padrão da amostra s = 200 horas. Supõe-se que o tempo de operação das lâmpadas
em geral tenha distribuição aproximadamente normal. Estime a vida média de operação de
lâmpadas da qual foi extraída a amostra, usando um intervalo de confiança de 95% (3.857
a 4.143 horas).
O desvio padrão da vida útil de uma determinada marca de tubo de imagem de TV é
conhecido e é igual a σ = 500, mas que a média da vida útil é desconhecida. Supõe-se que
a vida útil dos tubos de imagem tem uma distribuição aproximadamente normal. Para uma
amostra de n = 15, a média da vida útil é X = 8.900 horas de operação. Construir:
a) um intervalo de confiança de 95% (8.647 a 9.153)
b) de 90% para estimar a média da população. (8.687 a 9.113)
Referente exerc. 3, suponha que a vida útil dos tubos não possa ser considerada como
normalmente distribuída. Contudo a média da amostra X = 8.900 horas está baseada
numa amostra de n = 35. Construir um intervalo de confiança de 95% para estimar a
média da população. (8734 a 9066)
山村
42
5. Ref. exerc. 4, suponha que a população possa ser considerada normalmente distribuído,
mas que o desvio padrão da população seja desconhecido. Em lugar disso, suponha um
desvio padrão da amostra s = 500 e X = 8.900. Estimar a média da população, usando um
intervalo de confiança de 90%.(8.761 a 9.039)
6. Suponha que a população não possa ser considerada normalmente distribuída e que, além
disso, o σ populacional seja desconhecido. Se n = 35, s = 500 e X =8.900, estimar a
média da população utilizando um intervalo de confiança de 99%. (8.682 a 9.118)
7. Um analista de mercado obtém dados de uma amostra de 100 consumidores de um total de
400 que adquiriram uma oferta especial. As 100 pessoas gastaram, na loja, uma média de
X =$ 24,57 com um desvio padrão de s = $ 6,60. Usando um intervalo de 95% de
confiança, estimar:
a) O valor médio de compras para todos os 400 clientes,
b) O valor total das compras dos 400 clientes (23,45 a 25,69; 9.380 a 10.276)
8. Um comprador potencial deseja estimar o valor médio das compras por cliente em uma
loja de brinquedos em um aeroporto. Com base em dados de outros aeroportos similares, o
desvio padrão de tais valores de vendas é estimado em cerca de σ=$0,80. Qual o tamanho
mínimo que deveria Ter uma amostra aleatória se ele deseja estimar a média das vendas
dentro de $ 0,25 com confiança de 99% (69)
9. Um comprador potencial de uma loja de brinquedos observa uma amostra aleatória de n =
64 e acha a média da amostra X = $4,63 e o desvio padrão da amostra s=1,20. Determinar
o intervalo de confiança de tal sorte que o valor mínimo da média da população seja
identificada com um grau de confiança de 95% (é igual ou maior a 4,38).
10. Com um nível de confiança de 99%, qual a estimativa do valor máximo da média dos
valores de venda, ref. exerc. 9? (não é maior do que 4,98)
11. Construa intervalos de confiança para estimar a média da vida útil de uma marca de tubos
de imagens para TV com base de que a vida útil de todos os tubos tinha distribuição
aproximadamente normal. Dada uma amostra de n = 15 com X = 8.900 horas e s = 500.
a) Construir um intervalo de confiança de 95% para estimar a média da população (8623
a 9177)
b) Construir um intervalo de 90% para estimar a média da população.(8672 a 9128)
12. Um encarregado de compras de um supermercado toma uma amostra aleatória de 12 latas
tipo L de vagens em conserva. O peso líquido de cada lata de vagens está na tabela abaixo.
Determinar:
a) O peso líquido médio das vagens enlatadas da amostra
b) O desvio padrão da amostra
c) Supondo que o peso líquido médio por lata seja normalmente distribuído, estimar o
peso líquido médio das vagens usando um intervalo de confiança de 95%.(15,97;
0,15; 15,88 a 16,06)
Peso líquido de vagens enlatadas tipo L
Peso por lata
15,7
15,8
15,9
16,0
16,1
16,2
Número de latas
1
2
2
3
3
1
13. Estime a média de vendas, por estabelecimento varejista, durante o último ano, de um
determinado produto. O número de estabelecimentos varejistas é bastante grande.
Determinar o intervalo de confiança de 95% dado que os valores de venda são
considerados normalmente distribuídos, X = 3.425, σ= 200, n = 25 (3.346,60 a 3.503,40)
14. Ref: 13, Determine o mínimo valor da média usando um intervalo de confiança de
95%.( µ ≥ 3359
山村
43
15. Ref. 13, determinar o intervalo de confiança de 95%, dado que a população é
normalmente distribuída, X = 3 425, s = 200, n = 25 ( 3342,44 a 3507,56)
16. Ref. 13, determinar o intervalo de confiança de 95%, dado que a população não é
normalmente distribuída, X = 3 425, s = 200, n = 50.(3369,55 a 3480,45)
17. Para uma amostra de 50 firmas tomada de uma determinada indústria, o número médio
de empregados por firma é 420,4 com um desvio padrão da amostra de 55,7. Nesta
indústria, há um total de 380 firmas. Determinar:
a) O erro padrão da média, (7,33)
b) Determinar o intervalo de confiança de 90% para estimar o número médio de
trabalhadores por firma na indústria, (408,3 a 432,5)
c) Determinar o intervalo de confiança de 90% para estimar o número total de
empregados na indústria. (155154 a 164350) Obs: z = l.645
18. Um analista de departamento de pessoal seleciona aleatoriamente os registros de 16
empregados e acha que a taxa média de salário por dia é $ 7,50. Supõe-se que os salários
na firma sejam distribuídos normalmente. Se o desvio padrão dos salários é conhecido, e
igual a $ 1,00, estimar a taxa média de salários na firma usando um intervalo de
confiança de 80%(7,18 a 7,82)
19. Ref. 18, suponha que o desvio padrão da população seja desconhecido, mas que o desvio
padrão da amostra é $ 1,00. Estime a taxa média de salário na firma usando um intervalo
de confiança de 80%. (7,16 a 7,84)
20. O diâmetro médio de uma amostra de n = 12 bastões cilíndricos incluídos num
carregamento é de 2,350 mm com um desvio padrão de 0,050 mm. A distribuição dos
diâmetros dos cilindros de todos os bastões incluídos no carregamento é
aproximadamente normal. Determinar o intervalo de confiança de 99% para estimar o
diâmetro médio de todos os bastões incluídos no carregamento. (2,307 a 2,393)
21. Determine o valor máximo do diâmetro médio de todos os bastões incluídos no
carregamento. µ ≤ 2,388
22. Um restaurante pode acomodar 50 clientes. A experiência mostra que 10% dos que
fazem reserva não comparecerão. Suponha que o restaurante aceite 55 reservas. Calcule
a probabilidade de que o restaurante possa acomodar todos os clientes que
50,5 − 49,5
comparecerem.(µ=np=55.0,9=49,5
;
σ = npq =2,2;
z=
=0,45;
2,2
P(X50)=0,67
23. A altura dos homens de uma cidade apresenta distribuição normal. Para estimar a altura
média da população, levantou-se uma amostra de 150 pessoas obtendo-se uma média de
172 cm e desvio padrão de 4,07. Determine um intervalo de confiança de 98% para
estimar a altura média da população. (171,22;172,77)
24. A experiência com trabalhadores de uma certa indústria indica que o tempo necessário
para que um trabalhador, aleatoriamente selecionado, realize uma tarefa é distribuído de
maneira aproximadamente normal, com desvio padrão de 12 minutos. Uma amostra de
25 trabalhadores forneceu uma média de 140 minutos. Determinar os limites de
confiança de 95% para a média da população de todos os trabalhadores que fazem aquele
determinado serviço. (135,3; 144,7)
25. Foram retiradas 25 peças da produção diária de uma máquina, encontrando-se para uma
certa medida uma média de 5,2 mm. Sabendo-se que as medidas têm distribuição normal
com desvio padrão 1,2 mm, construir intervalos de confiança para a média aos níveis de
90%, 95% e 99%. (4,81 a 5,59; 4,73 a 5,67; 4,58 a 5,82)
山村
44
26. De uma distribuição normal com σ2 = 1,96, obteve-se a seguinte amostra:
25,2; 26,0; 26,4; 27,1; 28,2; 28,4. Determine o intervalo de confiança para a média da
população aos níveis de 95% e 90%. (25,76 a 28; 25,84 a 27,82)
27. Colhida uma amostra de 30 peças, tivemos os seguintes pesos:
250 265 267 269 271 275 277 281 283 284 287 289 291 293 293 298 301 303 306 307 307
309 311 315 319 322 324 328 335 339.
Ao nível de 95% de confiança, determine se esta amostra satisfaz a especificação pela
qual o peso médio deve ser 300 kg. (288,33 a 304,93 – satisfaz)
28. Em uma fábrica, colhida uma amostra de certa peça, obtiveram-se as seguintes medidas
para os diâmetros:10 11 11 11 12 12 12 12 13 13 13 13 13 13 13 13 13 13 13 13 14 14
14 14 14 15 15 15 16 16. Construir um intervalo de confiança de 95% para estimar a
média da população. (12,6 a 13,66)
29. Construir intervalos de confiança para a média admitindo-se as seguintes distribuições
amostrais, ao nível de 95%:
a)
Classes
0 | 5
5 | 10
10 | 15
15 | 20
b)
Classes
15 | 18
18 | 21
21 | 24
24 | 27
27 | 30
30 | 33
f
2
3
5
2
f
8
9
12
15
7
4
c)
Classes
f
30.
31.
32.
33.
34.
2,2 | 6,2
3
6,2 | 10,2
4
10,2 |14,2
5
14,2 | 18,2
3
R: 7,26 a 13,58; 22 a 24,55; 7,98 a 12,67
Uma amostra de tamanho 9, extraída de uma população normal, acusa média 1,0 e s =
0,264. Construir intervalos de confiança de 98% e 95% para a média populacional (0,745
a 1,255: 0,797 a 1,203)
Uma máquina automática de refrescos é regulada de modo que a quantidade suprida de
cada vez tenha distribuição aproximadamente normal com desvio padrão de 1,3 dl.
Determinar um intervalo de 96% de confiança para a quantidade média de todos os
refrescos servidos, sabendo que uma amostra de 30 copos de refrescos acusou conteúdo
médio de 21,0 dl. (20,51 a 21,49)
Uma amostra de tamanho 20 de uma população normal produz média 32,8 e s = 4,51.
Construa um intervalo de confiança de 90% para a média populacional. (31,06 a 34,54)
Uma amostra aleatória retirados de uma população normal com desvio padrão 5,
apresentou os seguintes dados: 22, 17, 21, 24, 15, 18, 16, 19. Determine o intervalo de
confiança de 90% para a média populacional. (16,1; 21,9)
A tabela a seguir apresenta uma amostra aleatória selecionada em uma população normal
com desvio padrão de 2 unidades. Com base na tabela construa um intervalo de
confiança de 96% para a média populacional. (10,56;11,85)
山村
45
35.
36.
37.
38.
39.
40.
41.
42.
Classes
F
5 | 7
3
7 | 9
7
9 | 11
10
11 | 13
8
13 | 15
7
15 | 17
5
Procurando dimensionar a ajuda de custo para seus 50 vendedores, uma empresa
acompanhou os gastos de 15 vendedores e verificou uma despesa média de 20 u.m. Se a
empresa acredita que o desvio padrão para o gasto é de 2 u.m., determine um intervalo de
confiança de 98% para o gasto médio dos vendedores dessa firma. (18,98; 21,02)
Uma amostra aleatória de 15 peças produzidas por uma máquina forneceu um
comprimento médio de 20 mm, com desvio padrão de 0,1 mm. Supondo que o
comprimento das peças tenha distribuição normal de probabilidades, determine um
intervalo de confiança de 95% para o comprimento médio das peças produzidas por esta
máquina. (19,94; 20,06)
Uma amostra de 5 elementos selecionados de uma população normal de 200 elementos
apresentou os valores: 120, 98, 106, 145, 92. Calcular um intervalo de confiança de 95%
para a média da população. (112,2; 21,12; 89,58 a 138,42)
O controle de qualidade de uma empresa levantou uma amostra aleatória de 50 peças da
produção de uma máquina. Obteve um diâmetro médio de 42 mm com desvio padrão de
0,2 mm. A) Ao nível de confiança de 98%, qual o intervalo de confiança para o diâmetro
médio das peças produzidas pela máquina? B) A máquina está regulada quando fornece
estimativa máxima menor que 42,1 mm ao nível de confiança de 95%. Com base na
amostra selecionada, a máquina está regulada? (41,932 a 42,068; está, pois a estimativa
máxima é de 42,057)
Um fabricante de papel para impressoras possui um processo de produção que opera de
maneira contínua, através de um turno completo de produção. É esperado que o papel
tenha um comprimento de 11 polegadas e o desvio padrão conhecido seja 0,02
polegadas. A intervalos periódicos, são selecionadas amostras para determinar se o
comprimento médio do papel ainda se mantém igual a 11 polegadas ou se algo de errado
ocorreu no processo de produção para que tenha sido modificado o comprimento do
papel produzido. Se tal situação tiver ocorrido, deve-se adotar uma ação corretiva. Uma
amostra aleatória de 100 folhas foi selecionada e verificou-se que o comprimento médio
do papel era 10,998 polegadas. Estime com um intervalo de confiança de 95% o
processo de produção. (10,99408 a 11,00192; está operando de forma correta)
Uma amostra de quatro crianças de uma população (berçário de um hospital) acusou os
seguintes pesos ao nascer (em quilogramas): 3,1; 2,8; 3,6; 3,7. Se o desvio padrão da
população é 0,4, determine o intervalo de: a) 95%; de b) 99% de confiança para o peso
médio populacional ao nascer. (3,30±0,392; 3,30 ±0,514)
Extraiu-se uma amostra aleatória de cinco notas de uma grande turma: 58, 60, 53, 81 e
73. Calcule um intervalo de 95% de confiança para a média µ de toda a turma. (65±14).
Os tempos médios de reação de 30 motoristas selecionados aleatoriamente acusaram
média de 0,83 segundos e desvio padrão de 0,20 segundos. Determine um intervalo de
95% de confiança para o tempo médio de reação de toda a população de motoristas.
Selecionou-se a seguir, aleatoriamente, mais um motorista, que acusou tempo médio de
reação de 0,98 segundos. Isto é de surpreender? Justifique. (0,83±0,0747; não é de
surpreender: X − X = 0,15 , que é comparável com s= 0,20 [ o intervalo de confiança
(
)
山村
46
43.
44.
45.
46.
em (a) é irrelevante, porque é para a média populacional, e não para uma observação
única].
Ao planejar uma represa, o governo deseja estimar o benefício médio anual de irrigação
por acre, para os todos os fazendeiros da redondeza. Para tanto, toma uma amostra
aleatória de 25 lotes de um acre, obtendo um benefício médio de $ 8,10, com desvio
padrão de $ 2,40. Construa o intervalo de 99% de confiança. (maior que 6,90)
Em uma amostra de seis estudantes de uma turma de educação física, mediu-se a taxa de
pulso (batidas por minuto) antes e depois de uma corrida de 200m, com os seguintes
resultados. Calcule o intervalo unilateral de 95% de confiança para o aumento médio da
taxa de pulso.
antes
74
87
74
96
103
82
depois
83
96
97
110
130
96
R: aumento médio > 9,89
Aplica-se um teste de inteligência a uma amostra aleatória de 100 alunos de certa escola,
que fornece X = 112 e s=11. Qual é o intervalo de confiança de 95% para o QI médio na
escola, baseando-se nos valores da amostra? (110,2 a 113,8)
Um fiscal de um departamento de defesa do consumidor inspeciona o peso do pão
produzido em uma padaria e toma uma amostra aleatória de 15 pães de uma fornada. O
peso médio e o desvio padrão desses 15 pães foi de X = 15,8 e 0,3 onças,
respectivamente. Construir um intervalo de confiança de 95% para o peso médio da
produção total. Ele multa o estabelecimento se este intervalo não incluir 15, 6 onças.
(15,63 a 15,97; não multa)
山村
47
8.1
INTERVALOS DE CONFIANÇA PARA A DIFERENÇA ENTRE DUAS MÉDIAS
O intervalo é construído de maneira semelhante à utilizada na estimação da média,
porém o erro padrão é o erro padrão da diferença entre as médias. Sendo duas as amostras
envolvidas, a fórmula para estimar a diferença entre duas médias populacionais é para n ≥ 30
(X
1
σX
1− X 2
)
− X 2 ± zσ X 1 − X 2
= σ X2 1 + σ X2 2
n < 30,
1
1
)
− X 2 ± zs X 1 − X 2 onde:
s X 1 − X = s X2 1 + s X2 2
ou
2
população normalmente distribuído
gl = n1+n2 –2
gl ⇒ graus de liberdade
(X
σX =
(X
ou
σ1
n1
e
1
)
− X 2 ± t gl s X 1 − X 2
σX =
2
σ2
n2
ou
sX1 =
s1
n1
e
sX 2 =
s2
n2
EXERCÍCIOS
1. A média de salários semanais para uma amostra de n = 30 empregados em uma grande
firma é X = $ 180,00, com um desvio padrão amostral de s=$14,00. Em uma outra grande
empresa, uma amostra aleatória de n = 40 empregados apresentou um salário médio
semanal de $ 170,00, com um desvio padrão amostral de s= $ 10,00. Determine o
intervalo de confiança de 99% para estimar a diferença entre os salários médios semanais
das duas firmas. (2,23 a 17,77)
2. Para uma amostra aleatória de n = 10 lâmpadas, a vida média é X = 4.000 horas com
s=200 horas. Para outra marca de lâmpadas, uma amostra de n=8 apresentou uma média
amostral de X = 4 600 horas e um desvio padrão de s = 250. Supondo que a duração das
lâmpadas de ambas as distribuições seja normalmente distribuída, determine o intervalo
de confiança de 90% para estimar a diferença entre a vida média de operação das duas
marcas de lâmpadas. (-790 a -410)
3. Um analista de mercados obtém dados de uma amostra de 100 consumidores de um total
de 400 que adquiriram uma oferta especial. As 100 pessoas gastaram, na loja, uma média
de X = $ 24,57 com um desvio padrão de s=$6,60. Por outro lado, houve 900 clientes que
não compraram a oferta especial, mas que fizeram outras compras na loja sob o período
em consideração. Para uma amostra de 200 desses clientes, o valor médio das compras foi
X = $ 19,60 com um desvio padrão de s = $ 8,40.
a) Estimar o valor médio das compras para os clientes que não compraram a oferta
especial, usando um intervalo de confiança de 95% (18,58 a 20,62)
山村
48
b) estimar a diferença entre o valor médio das compras dos clientes que compraram a
oferta e dos que não compraram, empregando um intervalo de confiança de
90%.(3,70 a 6,24)
4. Estimar a diferença mínima entre a média de compras entre os clientes da oferta e os da
não oferta, construindo um intervalo de confiança de 90%.( ≥ 3,98)
5. Uma amostra aleatória de 50 famílias de uma comunidade A apresenta uma renda média
familiar de X = 13 800,00, com um desvio padrão de s=$2.200,00. Uma amostra aleatória
de 50 famílias de uma comunidade B apresenta uma média de X = 14 600,00 com um
desvio padrão de s = $ 2 800. Estimar a diferença na renda média familiar entre as duas
comunidades, utilizando um intervalo de confiança de 95%. (187,17 a - 1 787,17)
6. Estimar a diferença máxima entre os níveis médios de renda da primeira e da segunda
comunidade, construindo um intervalo de confiança de 95%.( ≤ 31,04)
7. Em uma fábrica de enlatados, o peso líquido médio, em 10 gramas, de vagens
acondicionadas em latas L, em uma amostra de n = 12 latas, é de X = 15,97, com um
desvio padrão de s = 0,15. Em outra unidade, para uma amostra de n=15 latas, é X =16,14
com um desvio padrão de s = 0,09. Supõe-se que a distribuição das quantidades enlatadas
seja aproximadamente normal. Usando um intervalo de confiança de 90% estimar a
diferença entre o peso líquido médio nas duas unidades enlatadoras. (-0,25 a - 0,09)
8. Uma amostra aleatória de 40 empregados do sexo masculino é tirada e o número de
ausência é de 60 horas. Uma amostra similar de 50 empregados do sexo feminino é tirada
e o número de ausências é de 60 horas. Admitindo-se que σ = 10, construir o intervalo de
confiança para a diferença das médias ao nível de 95% e 90%. (0,84 a 9,16; 1,52 a 8,48)
9. Dez lotes de terra são tratados com o fertilizante “A” e doze com o fertilizante “B”. O
rendimento médio dos primeiros lotes foi de 8 com desvio padrão de 0,4. O rendimento
dos segundos lotes foi de 6 com desvio padrão 0,2. Construir o intervalo de confiança para
a diferença das médias ao nível de 95% e 98%. (1,73 a 2,27; 1,67 a 2,33 )
10. Um curso de inglês foi dado a 18 estudantes por meio do método tradicional, obtendo-se
média 75 e desvio padrão de 5. Para um outro grupo de 15 estudantes deram o mesmo
curso por meio de um método mais moderno obtendo-se média 70 e desvio padrão 6.
Construir o intervalo de confiança para diferença das médias, ao nível de 97,5%. (0,33 a
9,67)
11. Duas populações normais independentes apresentam desvio padrão σ1 =5 e σ2= 2. Uma
amostra aleatória de 12 elementos da primeira população apresentou média 34 e uma
amostra de 8 elementos da segunda população 9,4. Calcule o intervalo de confiança de
98% para a diferença das médias da população. (20,86 a 28,36)
12. Uma amostra de 10 elementos selecionada ao acaso de uma população normal apresentou
média de 18 e desvio padrão de 3. Uma amostra de 15 elementos selecionada ao acaso de
outra população normal apresentou média de 25 e desvio padrão de 4. Supondo as
populações independentes calcule um intervalo de confiança de 95% para a soma das
médias da população. (40,11 a 45,89)
13. A demanda diária de um item do estoque distribui-se normalmente. A linha de produção
encarregada de fabricar esta peça tem produzido uma quantidade que se distribui
normalmente e cuja variabilidade depende de fatores como manutenção, treinamento de
mão de obra etc. Um levantamento amostral aleatório da demanda e da produção diária
apresentou os resultados:
Demanda: 150, 140, 138, 157, 169, 150
山村
49
Produção: 160, 140, 120, 100, 150, 130. Calcule um intervalo de confiança de 90% para a
média entre demanda e produção. A esse nível de confiança, é possível afirmar que a
demanda excede a produção em pelo menos 10 unidades? (-1,21 a 35,89; não)
14. Para avaliar o efeito de uma campanha de aptidão, uma universidade selecionou
aleatoriamente cinco empregados antes da campanha e outros cinco após a campanha. Os
pesos foram os seguintes (juntamente com as iniciais do empregado): Antes: JH: 168. KL:
195, MM: 155, TR: 183, MT: 169; Depois: LW: 183, VG: 177, EP: 184, JC: 162, MW:
180. A) Construa um intervalo de confiança para: (i) o peso médio antes da campanha, (ii)
o peso médio após a campanha, (iii) a perda média de peso durante a campanha. B)
decidiu-se então que um melhor planejamento amostral consistiria em fazer mensurações
nos mesmos indivíduos. Obtiveram-se os resultados: KL; 197, MT: 163, TR: 180, MM:
150, JH: 160. Com base nos dados referentes a esses cinco indivíduos, calcule um
intervalo de 95% de confiança para a perda média de peso durante a campanha. (174±19,
170±18, 4±22, 4±5)
15. Mediu-se a capacidade respiratória de cinco indivíduos selecionados aleatoriamente, antes
e depois de determinado tratamento. Construa um intervalo de 95% de confiança para o
aumento médio populacional da capacidade respiratória.
Antes
2750
2360
2950
2830
2260
depois
2850
2380
2930
2860
2330
R: 40±57,6
16. Numa faculdade, extraíram-se amostras independentes de professores e professoras que
acusaram os salários abaixo. Calcule um intervalo de 95% de confiança para a diferença
média entre os salários de professores e professoras
Mulheres
9
12
8
10
16
homens
16
19
12
11
22
R: 5±5,79
17.Para determinar qual o melhor de dois tipos de sementes, uma estação experimental
agrícola escolheu aleatoriamente sete lotes no Estado. Cada lote foi dividido em duas
partes iguais, jogando-se uma moeda para determinar, sem tendenciosidade, qual
receberia a semente tipo A, e qual o tipo B. As safras, em toneladas foram:
Município
Semente A
Semente B
88
82
B
66
68
R
121
109
T
106
95
S
116
112
A
79
76
M
89
81
C
Que tipo de semente se afigura melhor? Construa um intervalo de 95% de confiança
para justificar sua resposta. ( a semente B é superior em 6 t/acre (mais ou menos 4,50
com 95% de confiança)
山村
50
18. Uma amostra aleatória de salários de 10 professores acusou média anual de $16000; uma
amostra de salários de cinco professoras acusou média anual de $11000. A variância
conjunta (pooled) S p2 foi 11,7. Calcule um intervalo unilateral de 95% de confiança para
mostrar a diferença entre os salários dos homens e das mulheres.( µ1 − µ 2 > 1,7 )
山村
51
8.2
INTERVALOS DE CONFIANÇA PARA A PROPORÇÃO
Utilizando a Distribuição Normal
A distribuição de probabilidade aplicável a proporções é a distribuição binomial. A
utilização da distribuição normal como aproximação da binomial para a construção de
intervalos de confiança para proporções é apropriada quando:
n ≥ 30 e
tanto
np ≥ 5 como
nq ≥ 5
Dada uma proporção observada na amostra, p , o erro padrão estimado da proporção é
dado por:
a) população infinita
b) população finita: se n > 0,05 N, utilizamos o fator de correção
finita:
sp =
Logo:
8.3
pq
p.q N − n
sp =
n
n
N −1
p ± zs p , é o intervalo de confiança para a proporção populacional
INTERVALOS DE CONFIANÇA PARA A DIFERENÇA ENTRE DUAS
PROPORÇÕES POPULACIONAIS
(p
1
)
− p 2 ± zs p − p com s p − p = s 2p ⊕ s 2p
1
2
1
2
1
2
1. Uma empresa de pesquisa de mercado faz contato com uma amostra de 100 homens de
uma grande comunidade e verifica uma proporção de 0,40 na amostra que prefere lâminas
de barbear fabricadas pelo seu cliente em vez de qualquer outra marca. Calcule o intervalo
de confiança de 95% para a proporção de todos os homens da comunidade.(0,30 a 0,50)
2. Uma proporção de 0,40 dos homens de uma amostra aleatória de 100 em uma grande
comunidade prefere as lâminas de barbear fabricadas pelo firma do cliente. Em uma outra
comunidade, 60 homens em uma amostra aleatória de 200 preferem as mesmas lâminas.
Calcular o intervalo de confiança de 90% para a diferença na proporção das duas
comunidades que preferem as lâminas da firma do cliente. (0,003 a 0,197).
3. Um administrador de uma universidade coleta dados sobre uma amostra aleatória de
âmbito nacional de 230 alunos de cursos de Administração de Empresas e encontra que 54
de tais estudantes têm diplomas de Técnico de Contabilidade. Usando um intervalo de
confiança de 90% estimar a proporção nacional de estudantes que possuem diplomas de
Técnico de Contabilidade (0,19 a 0,28)
4. Idem, 3; calcular a proporção mínima de estudantes que tenham diploma de Técnico de
Contabilidade, usando um intervalo de confiança de 90%.(0,199 ou mais)
5. Em uma grande área metropolitana em que estão localizados 800 postos de gasolina, por
uma amostra aleatória de 36 postos, 20 comercializam um determinado óleo lubrificante
que tem publicidade nacional. Usando um intervalo de confiança de 95%.
a) Estimar a proporção de todos os postos de gasolina daquela área metropolitana que
comercializam o óleo.
b) O número total de postos de serviço da área que comercializam o óleo 0,40 a 0,72;
320 a 576)
山村
52
6. Na tentativa de medir a tendência dos votantes sobre uma proposta de obrigações
escolares, um superintendente coleta amostras aleatórias de n = 100 em cada um dos
principais bairros residenciais incluídos no distrito escolar. Na primeira área 70 dos 100
eleitores amostrados indicaram que pretendiam votar a favor da proposta, enquanto, no
segundo bairro, 50 dos 100 revelarem tal intenção. Estimar a diferença entre as proporções
populacionais dos eleitores nas duas áreas, usando um limite de confiança de 95%. (0,07 a
0,33)
7. Para uma amostra aleatória de 100 domicílios em uma grande área metropolitana, o
número de domicílios nos quais ao menos um adulto se encontra atualmente
desempregado procurando emprego é 12. Estimar o intervalo de confiança de domicílios
na área, nos quais há pelo menos um adulto desempregado utilizando um intervalo de
confiança de 95% (5,7 a 18,3%)
8. Em contraste com o ex. anterior uma amostra aleatória de 100 domicílios em uma segunda
área metropolitana apresentou somente 6 domicílios, nos quais pelo menos um adulto está
desempregado e procurando emprego. Estimar a diferença na porcentagem de domicílios
que incluem um desempregado adulto, nas duas áreas, usando um intervalo de confiança
de 95%(-0,6 a 12,6%)
9. Ref. ex. anterior, qual a máxima porcentagem pelo qual o desemprego na primeira área
metropolitana excede a porcentagem de desemprego da segunda área, utilizando um
intervalo de confiança de 90%. ( ≤ 11,1%)
10. Em uma população, a proporção de pessoas favoráveis a uma determinada lei é de 40%.
Retiramos uma amostra de 300 pessoas dessa população. Determinar o intervalo de
confiança de 95%. (0,3445, 0,4555)
11. Deseja-se saber qual a proporção de pessoas da população portadoras de determinada
doença. Retira-se uma amostra de 400 pessoas, obtendo-se 8 portadores da doença.
Definir limites de confiabilidade de 99% para a proporção populacional. (0,002;0,038)
12. Em uma linha de produção de certa peça mecânica, colheu-se uma amostra de 100 itens,
constatando-se que 4 eram peças defeituosas. Construir o IC para a proporção das peças
defeituosas com confiança de 90%. (0,00786; 0,07214)
13. Em uma pesquisa de opinião, entre 600 pessoas pesquisadas, 240 responderam “sim” a
determinada pergunta. Estimar a porcentagem de pessoas com essa mesma opinião na
população, dando um intervalo de 95% de confiabilidade. (0,3608; 0,4392)
14. Uma votação realizada entre 400 eleitores, escolhidos ao acaso dentre todos os eleitores
de um determinado distrito, indicou que 55% deles são a favor do candidato A.
Determinar os limites de confiança de 99% para a proporção de todos os eleitores do
distrito favoráveis ao candidato A. Se o número de eleitores desse distrito fosse de
230.000 pessoas, qual seria a votação esperada do candidato A? (48,6%; 61,4%; 111.734;
141.266)
15. Uma pesquisa junto a 1500 eleitores acusou 720 votos para o candidato A e os restantes
780 para o candidato B. Calcule o intervalo de confiança de 95% para a proporção
populacional de eleitores favoráveis ao candidato A.(45% a 51%)
16. Um guarda de trânsito vistoriou 200 carros em um bairro da cidade e constatou que 25
motoristas não estavam usando cinto de segurança no momento da vistoria. Determine um
intervalo de confiança de 95% para a proporção de motoristas que usam regularmente o
cinto de segurança neste bairro. (0,7534 a 0,9966)
17. Uma amostra de 90 pessoas foi selecionada ao acaso de um grupo de 1.000 pessoas,
fornecendo a proporção de fumantes 0,24. Calcular o intervalo de confiança ao nível de
92% para a proporção de fumantes nas 1.000 pessoas. (0,1648 a 0,3152)
山村
53
18. Um vendedor consegue entrevistar 120 pessoas num dia, e resolve testar a aceitação de
um novo produto. Para isto, escolheu ao acaso 32 pessoas e mostrou o produto,
conseguindo uma proporção positivas de 25%. Qual seria a estimativa da proporção de
respostas positivas entre as 120 pessoas, ao nível de 85%? (0,1552 a 0,3448)
19. Numa cidade há 12.000 eleitores inscritos para a próxima eleição. Uma pesquisa pretende
estimar a proporção de eleitores que tencionam votar no candidato da oposição e para isso
levanta ao acaso uma amostra de 60 eleitores, obtendo uma proporção de 38%. Ao nível
de confiança de 98% qual o intervalo de confiança para a proporção de eleitores que
tencionam votar nesse candidato? (0,2334 a 0,5260)
20. Uma máquina produz uma peça que deve ser testada periodicamente para avaliar a
regulagem da máquina. A máquina é considerada regulada, se a proporção de peças
defeituosas na produção for de no máximo 4%. O último levantamento efetuado em 100
peças escolhidas ao acaso mostrou uma proporção de defeituosas de 3%. Ao nível de
confiança de 95% a proporção indica seguramente a regulagem da máquina? (não, pode
apresentar proporção de peças defeituosas superior a 4)
21. Uma revista semanal, em artigo sobre a participação das mulheres em curso superior de
Administração, afirmou que atualmente a proporção de mulheres neste curso é superior à
dos homens. Uma pessoa interessada em testar esta afirmação levantou uma amostra ao
acaso de 100 estudantes de administração e obteve na amostra uma porcentagem de 40%
de mulheres. Qual o intervalo de confiança para a proporção de mulheres na população ao
nível de 98%. A afirmação da revista é certamente falsa? (0,2859 a 0,5114, não a
proporção pode ser maior que 50%).
22. Para definir as cores dos carros da linha a ser lançada no próximo ano, uma montadora
selecionou 200 pessoas e apresentou protótipos em diversas cores, anotando a preferência
das pessoas. Setenta destas pessoas preferiram uma nova cor perolada, e a montadora
deseja estimar com 80%, qual a proporção de carros desta cor que serão solicitados no
próximo ano. Qual deve ser a estimativa? (0,3068 a 0,3962)
23. Em uma população, a proporção de pessoas favoráveis ao candidato A é de 0,40. Retirada
uma amostra de 300 pessoas dessa população, determine o intervalo de confiança de 95%.
(0,3445 a 0,4555)
24. O gerente de produção de um jornal na cidade deseja estimar a proporção de jornais
impressos que apresentam algum tipo de problema, tal como excesso de tinta, montagem
de páginas inapropriadas, falta de páginas, páginas duplicadas e assim por diante.
Experiências do passado envolveram o exame detalhado do primeiro jornal que sai da
impressora, porém nenhuma avaliação posterior era feita dos jornais impressos. O gerente
de produção determinou que fosse selecionada para análise uma amostra aleatória de 200
jornais. Suponha que, dessa amostra de 200, 35 contêm algum tipo de problema. Se o
gerente deseja ter 90% de confiança na estimativa da real proporção da população, qual é
esse intervalo? (0,13 a 0,22)
25. Examinam-se 98 animais, encontrando-se 53 infectados com determinado vírus. Construir
um intervalo de 95% de confiança para a proporção populacional de animais infectados.
(use 3 casas decimais, 0,442; 0,640)
26. Entrevistaram-se em uma cidade 1500 pessoas em idade de trabalho e constata-se que 145
estão desempregadas. a) estimar a taxa de desemprego com base nos dados (0,097). b)
estabelecer um intervalo de 95% de confiança para a taxa populacional (0,082; 0,112)
27. Fez-se uma análise de 44 trabalhos de pesquisa que utilizaram experimentos clínicos
aleatorizados, para comparar um novo tratamento (I) com um tratamento padrão (S) em
cirurgia e anestesia. Em 23 das pesquisas (I) foi preferido (e nos outros 21 estudos, S foi
山村
54
preferido ). Admitindo que os 44 trabalhos representem uma amostra aleatória da
população de todos os trabalhos na área, construa um intervalo de confiança para a
proporção populacional onde I é preferido a S. (0,523±0,148)
28. Fez-se uma experiência em larga escala para testar a eficiência de uma nova vacina contra
P. De 740 000 crianças do segundo grau em todo o país, 400000 se apresentaram como
voluntárias. Metade dos voluntários, selecionados aleatoriamente, recebeu a vacina: à
outra metade foi administrado um substituto (inócuo) de água e sal. Os resultados foram:
Grupo
Vacinadas
Substitutivo (controle)
recusas
Número de crianças
200 000
200 000
340 000
Número de casos de pólio
57
142
157
a) Para cada um dos três grupos, calcule a taxa de incidência de pólio (casos por
100.000),
b) Estime a redução na taxa de incidência de pólio produzida pela vacina, incluindo
um intervalo de 95% de confiança,
c) Suponha que todos os voluntários tivessem sido vacinados, ficando as recusas
como grupo de controle: que tipos de dados seriam obtidos?
R: 28,5; 71,0; 46,2 (POR 100 000); estimamos que a vacina reduz a taxa de incidência
de 71 para 29 casos por 100 000, uma redução de 42 casos em 100000 (com 95% de
confiança, uma redução de 42±14); tal estudo observacional teria confundido o efeito do
voluntariado com vacina (os voluntários têm quase o dobro da taxa de pólio dos nãovoluntários (71 vs 46 por 100 000).
9
APLICAÇÕES DA ESTIMATIVA EM AUDITORIA
Pode-se definir auditoria como a coleta e avaliação de evidências sobre informações
numéricas relacionadas a uma entidade econômica, com o objetivo de determinar ou elaborar
relatórios sobre a correlação entre as informações numéricas obtidas e os critérios
estabelecidos.
É amplamente aceito, no campo da auditoria, que 100% do exame dos itens tornam-se
antieconômicos e sem garantias. Entre as vantagens da amostragem estatística, destacam-se:
1. O resultado da amostragem é objetivo e tem respaldo legal. Como o tamanho da
amostra baseia-se em princípios estatísticos demonstráveis, a auditoria é respaldada
por superiores hierárquicos e pela própria Justiça.
2. O método oferece uma maneira de calcular o tamanho da amostra antecipadamente,
numa base objetiva.
3. O método fornece uma estimativa do erro de amostragem.
4. Este método pode vir a ser mais apurado, no que diz respeito a tirar conclusões sobre
a população, uma vez que o exame de grandes populações pode demandar tempo e
pode estar sujeito a um maior volume de erro do que uma amostra estatística.
5. Amostras estatísticas podem ser combinadas e avaliadas, mesmo quando executadas
por diferentes auditores. Isso ocorre porque existe uma base científica para a
amostragem, de modo que se pode considerar que as amostragens tenham sido
realizadas por um único auditor.
山村
55
6. A avaliação objetiva dos resultados de uma é possível. Os resultados podem ser
projetados, com um erro de amostragem conhecido.
Estimando o total da população
Em aplicações de auditoria, de maneira geral estamos mais interessados em obter estimativas
do total da população do que a média da população.
O total é igual ao tamanho da população multiplicado pela média aritmética da amostra.
Total=N X ; assim sendo, a estimativa do intervalo de confiança para o total pode ser obtida:
S N −n
N X ± Ntn −1
n N −1
Exemplo: Suponha que um auditor está diante de uma população de 5000 notas fiscais e
deseja calcular o valor total da população. Uma amostra de 100 notas fiscais é selecionada,
com os seguintes resultados:
Valor médio das notas fiscais: $ 1076,39; desvio padrão: $ 273,62
Temos: Total=(5000)(1076,39)=5 381 950
A estimativa do intervalo de confiança do valor total da população:
273, 62 5000 − 100
(5000)(1076,39) ± (5000)(1,9842)
5000 − 1
100
5113206,19 ≤ Total da população ≤ 5 650 693,81
Estimativa da diferença:
é utilizada quando um auditor acredita que existem erros em um conjunto de itens que estão
sob auditoria e deseja calcular a magnitude desses erros, com base numa amostra.
A diferença média é igual a soma das diferenças, dividida pelo tamanho da amostra:
n
D=
∑ Di
i =1
n
; o desvio padrão das diferenças é S D =
∑ Di2 − nD
2
i =1
n
n −1
Cada item sem uma diferença tem um valor igual a zero. O intervalo de confiança da
S
N −n
diferença total na população: N D ± N (tn −1 ) D
n N −1
Supondo que na amostra de 100 notas fiscais existam 14 erros:
75,41 38,97 108,54 -37,18 62,75 118,32 -88,84 127,74 55,42 39,03
29,41 47,99
28,73 84,05
n
Temos: D =
∑D
i =1
n
i
=6,9034, SD= 27,23 e
27, 23 5000 − 100
5000 − 1
100
7 772,27 ≤ diferença total ≤ 61 261,73
(5000)(6,9034) ± 5000(1,9842)
山村
56
REFERÊNCIAS
BARBETTA, P. A. Estatística aplicada às Ciências Sociais. 3. ed. Florianópolis: UFSC,
1999.
BUSSAB, W. O., MORETTIN, P. A. Estatística básica. 5. ed. São Paulo: Saraiva, 2002.
COSTA NETO, P. L. O. Estatística. São Paulo: Edgard Blücher, 1977.
DOWNING, Douglas. Estatística aplicada. São Paulo: Saraiva, 1998.
FONSECA J. S.; et al. Curso de Estatística. 5. ed. São Paulo: Atlas, 1994.
FONSECA, J. S.; et al. Estatística aplicada. 2. ed. São Paulo: Atlas, 1986.
HOEL, P. G. Estatística elementar. São Paulo: Atlas, 1981.
HOFFMANN, R. Estatística para economistas. 3. ed. São Paulo: Pioneira, 1998.
KASMIER, L. J. Estatística aplicada a economia e administração. São Paulo: McGrawHill, 1982.
LAPPONI, J. C. Estatística usando Excel 5 e 7. São Paulo: Lapponi treinamento e Editora,
1997.
LEVINE, D. M., BERENSON, M. L., STEPHAN, D. Estatística: Teoria e Aplicações. Rio
de Janeiro: LTC, 2000.
LOPES, P. A. Probabilidades e Estatística. Rio de Janeiro: Reichamann & Affonso
Editores, 1990.
MATTAR, F. N. Pesquisa de Marketing: metodologia, planejamento. 5.ed. v1, v2. São
Paulo: Atlas, 1999.
MILONE, G.; et al. Estatística geral. São Paulo: Atlas, 1993.
MOORE, David. A Estatística básica e sua prática. Rio de Janeiro: LTC, 2000.
MORETTIN, L. G. Estatística básica. v1,v2. São Paulo: Makron Books, 2000.
PEREIRA, W. Estatística: conceitos básicos. São Paulo: McGraw-Hill, 1990.
RICHARDSON, R. J.; et al. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 1999.
SILVA, E. M. da; et al. Estatística: para os cursos de economia, administração e ciências
contábeis. v1, v2. São Paulo: Atlas, 1995.
SILVER, Mick. Estatística para Administração. São Paulo: Atlas, 2000.
SMAILES J.; et al. Estatística aplicada à administração com Excel. São Paulo: Atlas,
2002.
SOARES, J. F.; et al. Introdução à Estatística. Rio de Janeiro: LTC, 1991.
SPIEGEL, M. R. Estatística. 2. ed. São Paulo: McGraw-Hill, 1985.
SPIEGEL, M. R. Probabilidade e Estatística. São Paulo: McGraw-Hill, 1978.
STEVENSON, W. J. Estatística aplicada à administração. São Paulo: Harper & Row do
Brasil, 1981.
TIBONI, C. G. R. Estatística básica para o curso de turismo. São Paulo: Atlas, 2002.
TOLETO, G. L.; et al. Estatística básica. 2. ed. São Paulo: Atlas, 1985.
TRIOLA, M. F. Introdução à Estatística. 7.ed. Rio de Janeiro: LTC, 1998.
VIEIRA, S. Elementos de estatística. São Paulo: Atlas, 1986.
WONNACOTT, R. J.; et al. Fundamentos de estatística. Rio de Janeiro: LTC, 1985.
山村