probabilidade dada distribuição

6.7 – A DISTRIBUIÇÃO NORMAL DE PROBABILIDADE
A distribuição normal de probabilidade é uma distribuição de probabilidade
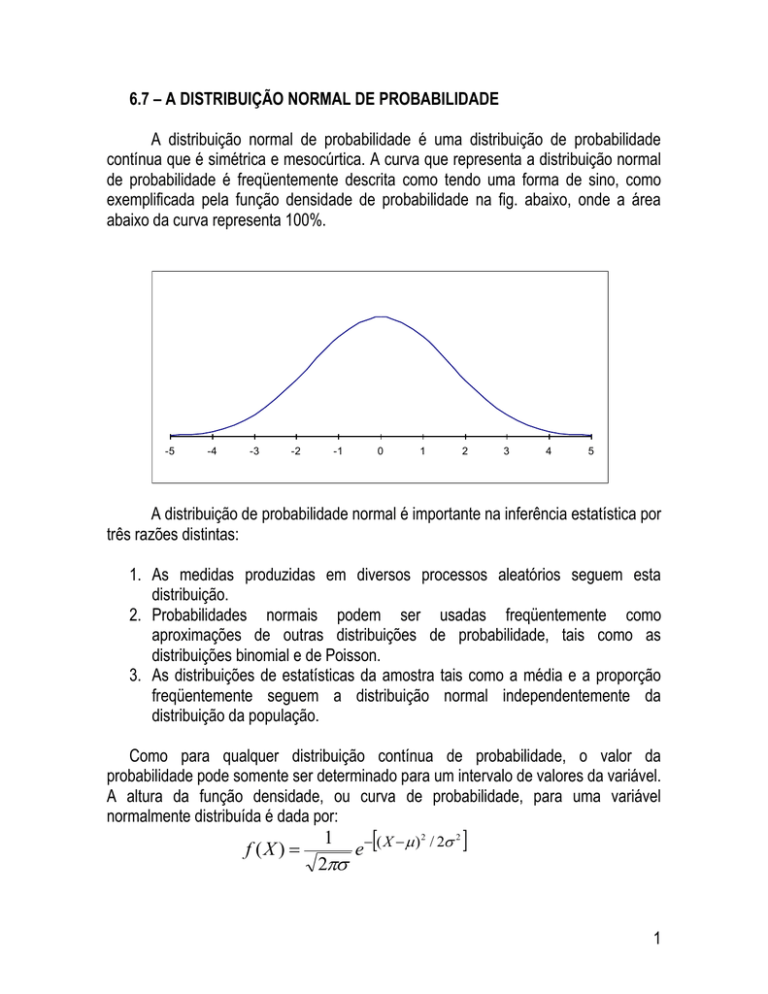
contínua que é simétrica e mesocúrtica. A curva que representa a distribuição normal
de probabilidade é freqüentemente descrita como tendo uma forma de sino, como
exemplificada pela função densidade de probabilidade na fig. abaixo, onde a área
abaixo da curva representa 100%.
-5
-4
-3
-2
-1
0
1
2
3
4
5
A distribuição de probabilidade normal é importante na inferência estatística por
três razões distintas:
1. As medidas produzidas em diversos processos aleatórios seguem esta
distribuição.
2. Probabilidades normais podem ser usadas freqüentemente como
aproximações de outras distribuições de probabilidade, tais como as
distribuições binomial e de Poisson.
3. As distribuições de estatísticas da amostra tais como a média e a proporção
freqüentemente seguem a distribuição normal independentemente da
distribuição da população.
Como para qualquer distribuição contínua de probabilidade, o valor da
probabilidade pode somente ser determinado para um intervalo de valores da variável.
A altura da função densidade, ou curva de probabilidade, para uma variável
normalmente distribuída é dada por:
f (X ) 
2
2
1
e( X   ) / 2 
2
1
onde  é a constante 3,1416; e é a constante 2,7183;  é a média da distribuição;
e  é o desvio padrão da distribuição. Uma vez que cada combinação de  e 
geraria uma distribuição normal de probabilidade diferente (todas simétricas e
mesocúrticas), as tabelas de probabilidades da normal são baseadas em uma
distribuição particular: a distribuição normal padronizada. Esta é a distribuição normal
de probabilidade com   0 e   1 . Qualquer conjunto de valores X normalmente
distribuído pode ser convertido em valores normais padronizados z pelo uso da
fórmula:
z
X 

Existem tabelas que indicam as proporções de área para vários intervalos de
valores para a distribuição de probabilidade normal padronizada, com a fronteira
inferior do intervalo começando sempre na média. A conversão dos valores dados da
variável X em valores padronizados torna possível o uso desta tabela, e faz com que
seja desnecessário o uso da equação da função densidade de qualquer distribuição
normal dada.
VALOR ESPERADO E(x)
E (x)  
VARIÂNCIA V(x)
V ( x)   2
Ex 1. Sabe-se que a vida útil de um componente elétrico segue uma
distribuição normal com média igual a 2000 horas e desvio padrão de 200
horas.
Calcular a probabilidade de que um componente aleatoriamente selecionado dure:
a) Entre 2000 e 2400 horas
b) Mais de 2200 horas
c) Menos de 2200 horas
d) Entre 1800 e 2300 horas
e) Mais que 1875 horas
Ex 2. Os resultado de um exame nacional para estudantes recém-formados
apresentaram uma média de 5,0 com desvio padrão de 1,0 . Os resultados têm
uma distribuição aproximadamente normal. Qual a probabilidade de que o grau de
um indivíduo aleatoriamente escolhido esteja;
a) Entre 5,0 e 6,5
b) Entre 4,5 e 6,0
c) Entre 7,5 e 8,5
d) Inferior a 3,0
2
Ex. 3 A vida útil de uma certa marca de pneus radiais tem uma distribuição
normal com média de 38.000 km e desvio padrão de 3.000 km. a) Qual a
probabilidade de que um pneu aleatoriamente escolhido tenha uma vida útil de
no mínimo 35.000 km? b) Qual a probabilidade de que ele dure mais de
45.000 km? c) Se um comerciante encomenda 500 pneus para revende-los.
Qual a quantidade aproximada de pneus que terá uma vida entre 40000 e
45000 km?
Ex 4. O tempo necessário para o atendimento de uma pessoa em um guichê
de um banco tem distribuição aproximadamente normal com média de 130 s e
desvio padrão de 45 s. Qual a probabilidade de que um indivíduo
aleatoriamente selecionado a) requeira menos de 100 segundos para terminar
suas transações. b)Gaste entre 2 e 3 minutos no guichê?
Ex 5. Suponha que os diâmetros de parafusos produzidos por uma fábrica
sejam normalmente distribuídos com média 0,25 polegadas e o desvio-padrão
0,02 polegadas. Um parafuso é considerado defeituosos se seu diâmetro é
menor ou igual a 0,20 polegadas ou maior ou igual a 0,28 polegadas. Encontre
a porcentagem de parafusos defeituosos produzidos pela fábrica.
Ex 6. Suponha que as notas de um exame são normalmente distribuídas com
média 7,6 e desvio padrão de 1,5. 15% dos estudantes mais adiantados
recebem a nota A e 10% dos mais atrasados recebem a nota F. Encontre a) o
mínimo grau para receber um A e b) o mínimo grau para passar(não receber
um F)
Ex 7. O tempo necessário, em uma oficina, para o conserto de transmissão de
um tipo de automóvel é normalmente distribuído com média de 45 minutos e
desvio padrão de 8,0 min. O mecânico planeja começar o conserto do carro de
um cliente 10 minutos após o carro ter sido deixado na oficina, comunicando ao
cliente de que o carro estará pronto e um tempo total de uma hora. Qual a
probabilidade de que o mecânico esteja enganado?
Ex 8. Com referência ao problema anterior, qual a previsão de tempo de
trabalho para que haja 90 % de probabilidade de que o conserto da
transmissão se efetue dentro do tempo previsto?
3