Estatística - Distribuição Normal

Estatística - Distribuição Normal
Professor José Alberto - (11) 9.7525-3343
sosestatistica.com.br
1
Estatística - Distribuição Normal
1
A Distribuição Normal
Sem dúvida a mais importante das distribuições contínuas de probabilidade. Além de
descrever uma série de fenômenos físicos e financeiros, possui grande uso na estatística
inferencial.
É inteiramente descrita por seus parâmetros média µ e desvio padrão σ , ou seja,
conhecendo-se estes valores consegue-se determinar qualquer probabilidade em uma
distribuição Normal.
Cada valor de µ e/ou σ caracteriza uma curva de distribuição de probabilidade.
Porém, para se calcular uma probabilidade específica (área sob a curva normal), faz-se
uso de uma distribuição particular: a "distribuição normal padronizada". Para se obtêla quando temos uma distrbuição normal quaquer (µ 6= 0 e/ou σ 6= 1), devemos fazer
a seguinte transformação:
Z=
x−µ
σ
⇒
Z ∼ N(0, 1).
Assim, a distribuição passa a ter média µ = 0 e desvio padrão σ = 1. Por ser uma
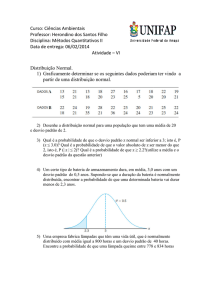
distribuição muito usada, existem tabelas a qual encontramos a resolução de suas integrais que equivalem as probabilidades desejadas. A Figura a seguir mostra algumas
áreas importantes:
Figura 1: Distribuição Normal
Exemplo: Suponha que a altura de uma determinada população segue uma distribuição Normal com µ = 170cm e σ = 6cm. Deseja-se saber a probabilidade de uma
pessoa ter mais de 176cm.
X − µ
176 − 170 P(X > 176) = P
>
= P(Z > 1) = 0, 5 − 0, 3413 = 0, 1587 ∼
= 16%
σ
6
Professor José Alberto
sosestatistica.com.br
(11)9.7525-3343