AULA 23 FUNÇÕES TRIGONOMÉTRICAS DE UM ÂNGULO

AULA 23
FUNÇÕES TRIGONOMÉTRICAS DE UM ÂNGULO AGUDO:
PROF. PAULO
AS RAZÕES TRIGONOMÉTRICAS
DEFINIÇÕES:
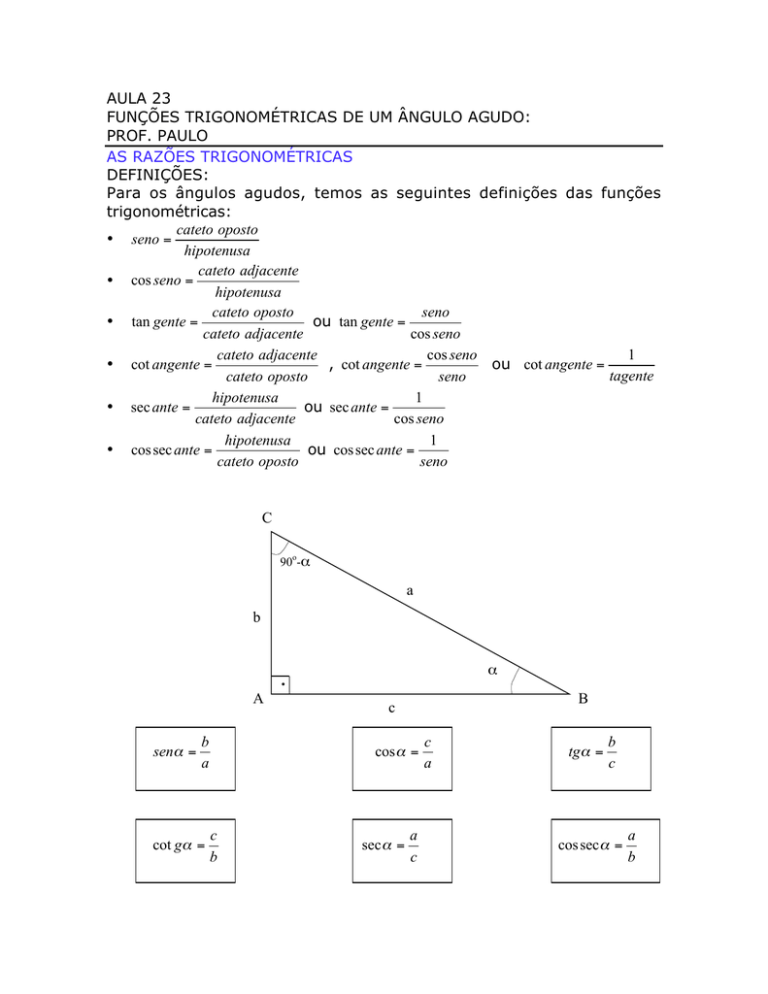
Para os ângulos agudos, temos as seguintes definições das funções
trigonométricas:
cateto oposto
• seno =
hipotenusa
cateto adjacente
• cos seno =
hipotenusa
cateto oposto
seno
• tan gente =
ou tan gente =
cos seno
cateto adjacente
1
cateto adjacente
cos seno
• cot angente =
, cot angente =
ou cot angente =
tagente
seno
cateto oposto
1
hipotenusa
• sec ante =
ou sec ante =
cos seno
cateto adjacente
1
hipotenusa
• cos sec ante =
ou cos sec ante =
seno
cateto oposto
C
90o-a
a
b
A
sena =
b
a
cot ga =
.
a
B
c
cos a =
c
b
sec a =
a
c
c
a
tga =
b
c
cos sec a =
a
b
Observação:
Das definições acima, temos:
(
)
sena = cos 90 0 - a =
b
a
(
)
cos a = sen 90 0 - a =
c
a
ÂNGULOS NOTÁVEIS
Os ângulos de 300, 450 e 600 são utilizados com muita freqüência e
por isso convém memorizá-los. Para isto temos uma tabela que resume
esses valores:
sen
cos
tg
300
1
2
450
2
2
2
2
1
3
2
3
3
600
3
2
1
2
3
OUTRAS RELAÇÕES TRIGONOMÉTRICAS
Na trigonometria temos uma relação muito importante chamada:
RELAÇÃO FUNDAMENTAL
Relações auxiliares:
sen 2a + cos 2 a = 1
tg 2a + 1 = sec 2 a
1 + cot g 2a = cos sec 2 a
ÏÔcos 2 a = 1 - sen 2a
Ì 2
ÔÓsen a = 1 - cos 2 a
Exemplos:
1) Calcule o seno, o cosseno , a tangente, a cotangente, a secante e a
cossecante de a na figura seguinte:
C
a
7
a
A
Resolução:
B
24
Inicialmente vamos calcular a hipotenusa.
a2 = 72 + 242 fi a2 = 625 \ a = 25
Então, temos:
7
7
sena = fi sena =
a
25
24
24
cos a =
fi cos a =
a
25
7
tga =
25
25
cot ga =
7
25
sec a =
24
25
cos sec a =
7
2) Uma pessoa sobe uma rampa de 10m de comprimento e se eleva
verticalmente 5m. Qual o ângulo que a rampa forma com o plano
horizontal?
Resolução:
10m
5m
q
.
Seja q a medida do ângulo procurado. Então, temos:
5
1
senq =
fi senq = \q = 30 0
10
2
3) Um observador enxerga uma montanha segundo um ângulo a.
Caminhando 420m em direção à montanha, passa a enxergá-la
segundo um ângulo b. Calcule a altura da montanha, sabendo que
1
2
tga = e tgb = .
2
3
h
a
b
420m
Resolução:
Observe, na figura, que:
h 2
3h
tgb = = fi x =
x 3
2
h
1
tga =
= fi 2h = x + 420
x + 420 2
x
(1)
(2)
De (1) e (2) temos:
2h -
3h
= 420
2
h
= 420 fi h = 840
2
Resposta: 840m.
1 - cos 2 x
4) Simplificando a fração
, obteremos:
senx
Resolução:
1 - cos 2 x sen 2 x
=
= senx
senx
senx
EXERCÍCIOS:
1) Calcule o seno, cosseno e a tangente de a e de b na figura a
seguir:
C
b
a
5
a
A
12
B
2) (Vunesp) Uma rampa lisa, de 20m de comprimento, faz um
ângulo de 300 com o plano horizontal. Uma pessoa que sobe esta
rampa inteira eleva-se verticalmente:
a)
b)
c)
d)
e)
17m
10m
15m
5m
8m
3) (Fuvest) Calcule x indicado na figura.
x
300
.
600
100m
y
4) (U.F.Viçosa) Satisfeitas as condições de existência, a expressão
Ê 1 - sen 2 x ˆ
˜˜. cos sec x , é idêntica a:
E = ÁÁ
Ë cot gx ¯
a)
b)
c)
d)
e)
senx
cosx
1
0
secx
.
1
, então o valor da expressão
2
E = cossecx + cosx.tgx é:
5
a)
2
3
b)
2
1
c)
2
6
d)
3
f) 1
5) Se 00<x<900 e senx =
Resolução dos exercícios:
1)
a 2 = 5 2 + 12 2 fi a 2 = 169 fi a = 13
5
12
5
, cos a =
e tga =
13
13
12
12
5
12
senb = , cos b =
e tgb =
13
13
5
sena =
2) Observe a figura:
sen30 0 =
20m
x
1
x
fi =
fi x = 10m
20
2 20
x
300
.
Resposta: b
3) Observe, na figura, que:
x
x
tg 60 0 = fi 3 = fi x = y 3
y
y
tg 30 0 =
(1)
x
3
x
fi
=
fi 3 x = (y + 100 ) 3 (2)
y + 100
3
y + 100
De (1) e (2) temos:
3 y 3 = (y + 100 ) 3
y = 50 fi x = 50 3
Resposta: 50 3m.
Ê 1 - sen 2 x ˆ
cos 2 x 1
˜˜. cos sec x =
4) E = ÁÁ
.
= cos x
cos x senx
Ë cot gx ¯
senx
Resposta : b
5)
0 0 < x < 90 0 ¸
Ô
0
˝ fi x = 30
1
senx =
Ô
2
˛
1
3
3
= 2, cos x =
e tgx =
senx
2
3
3 3
1 5
.
= 2+ =
Assim: E = 2 +
2 3
2 2
Resposta: a
portanto, cos sec x =