Material da aula 1

 PREPARATÓRIO PROFMAT/ AULA 8 Geometria QUESTÕES DISCURSIVAS
Questão 2. (PROFMAT-2011)
Considere um triângulo retângulo isósceles
ABC com hipotenusa BC. Tomando o ponto A como
centro e AB como raio, consideramos o arco de
circunferência delimitado pela corda BC.
Consideremos ainda a semicircunferência de
diâmetro BC, conforme a figura ao lado. Designamos
por T a área da região triangular ABC e por S e L as
áreas das outras duas regiões. Prove que L = T.
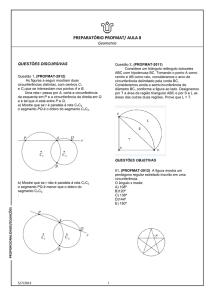
Questão 1. (PROFMAT-2012)
As figuras a seguir mostram duas
circunferências distintas, com centros C1
e C2 que se intersectam nos pontos A e B.
Uma reta r passa por A, corta a circunferência
da esquerda em P e a circunferência da direita em Q
e é tal que A está entre P e Q.
a) Mostre que se r é paralela à reta C1C2
o segmento PQ é o dobro do segmento C1C2 .
Atenção: a figura deve ser feita no caderno de
respostas
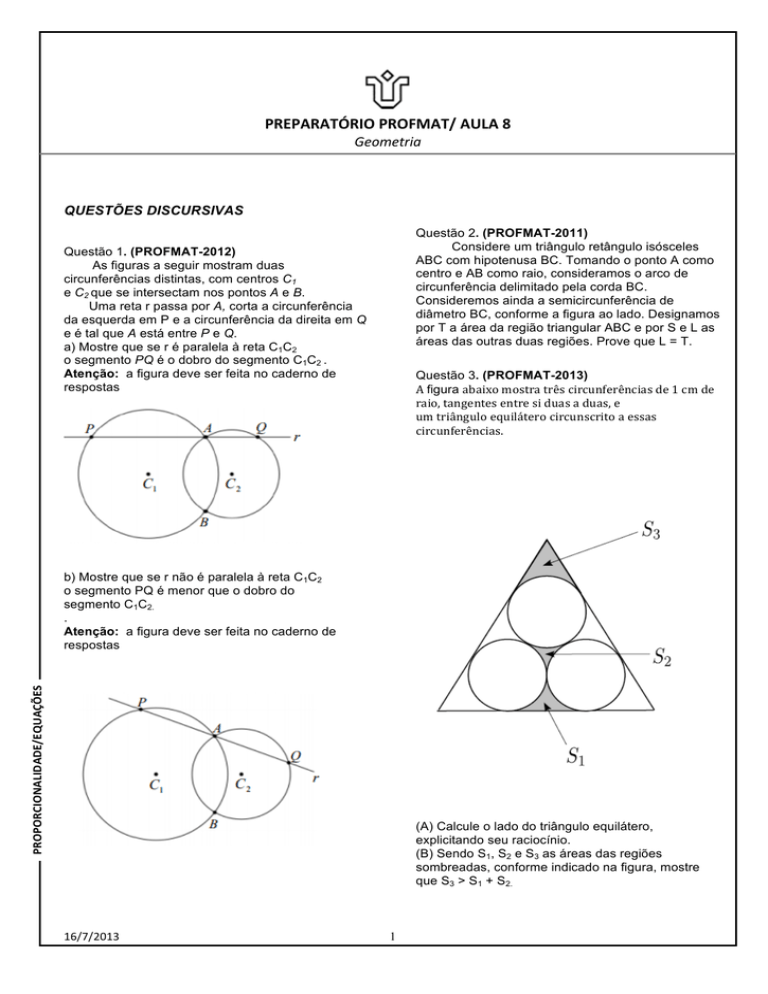
Questão 3. (PROFMAT-2013)
A figura abaixo mostra três circunferências de 1 cm de raio, tangentes entre si duas a duas, e um triângulo equilátero circunscrito a essas circunferências.
PROPORCIONALIDADE/EQUAÇÕES b) Mostre que se r não é paralela à reta C1C2
o segmento PQ é menor que o dobro do
segmento C1C2.
.
Atenção: a figura deve ser feita no caderno de
respostas
(A) Calcule o lado do triângulo equilátero,
explicitando seu raciocínio.
(B) Sendo S1, S2 e S3 as áreas das regiões
sombreadas, conforme indicado na figura, mostre
que S3 > S1 + S2.
16/7/2013
1
QUESTÕES OBJETIVAS
01. (PROFMAT-2012) Assinale, dentre as regiões a seguir, pintadas de cinza, aquela que é formada pelos pontos do quadrado cuja distância a qualquer um dos vértices não é maior do que o comprimento do lado do quadrado. 04. (PROFMAT-2013)
Sejam A e B dois pontos distintos no plano. O
conjunto dos pontos C desse plano tais que a área
do triângulo ABC é igual a 1 é
(A) uma reta.
(B) um par de retas.
(C) uma parábola.
(D) vazio.
(E) impossível de se determinar sem se conhecer A
e B.
02. (PROFMAT-2013)
Um círculo de raio R tem área A e, girando o círculo em torno de um diâmetro, obtemos uma esfera de volume V . Se repetirmos o procedimento com um círculo de raio 2,5R, sua área e o volume da esfera correspondente serão, respectivamente, (A) 2,5A e 2,5V (B) 5A e 25V (C) 5A e 10V (D) 6,25A e 12,25V (E) 6,25A e 15,625V 05. (PROFMAT-2013)
Um silo para armazenagem de grãos é feito de
metal e tem o formato de um cilindro medindo 2,5 m
de diâmetro e 6 m de altura. E preciso pintar a
superfície lateral externa (sem tampa ou fundo)
de três desses silos e a tinta indicada tem um
2
rendimento de 40 m por galão. Sabendo que serão
necessárias duas demãos de pintura em cada silo,
PROPORCIONALIDADE/EQUAÇÕES 03. (PROFMAT-2013)
A figura ao lado é composta por 4
qual é a melhor aproximação para a quantidade de
tinta necessária?
semicircunferências. As duas meno-
(A) 6 galões
res possuem o mesmo raio, medindo
(B) 9 galões
1,5 cm. A semicircunferência inter-
(C) 7 galões
mediária tem diâmetro igual ao raio
(D) 14 galões
da circunferência maior.
(E) 16 galões
2
A área da região sombreada, em cm , é
(A) 18 π
06. (PROFMAT-2013) Considere um triângulo
isósceles inscrito em um círculo de raio 3 metros,
como mostra a figura. Se x representa a medida,
em metros, da altura desse triângulo com relação
a sua base, então sua área, em metros quadrados,
é igual a
(A) X √x(6-x)
(B) X √x(3-x)
(B) 25,5 π
(C) 22,5 π
(D) 36 π
(E) 45 π
16/7/2013
2
2
(C) X √3 /2
(D) X/2 √x(6-x)
(E) X/2 √x(3-x)
09. (PROFMAT-2013)
O semicírculo da figura está inscrito no triângulo
retângulo ABC de catetos AB = 7 e BC = 24.
O raio do semicírculo é igual a
(A) 2√5
(C) 3√3
(E) 16/3
07. (PROFMAT-2013) . No retângulo ABCD da
Figura os triângulos cinzentos têm todos a mesma
área. Quanto vale AP / BP?
(A) 3/2
(C) √3
(E) 2
(B) 5
(D) 21/4
10. (PROFMAT-2013) . Em um triângulo retângulo
conhecem-se a soma s dos catetos e
altura h relativa à hipotenusa. Qual das expressões
abaixo representa o valor da hipotenusa em função
de s e h ?
(B) (1+ √5)/2
(D) 9/5
(A) s-h
2
2
(C) s+ √(h –s )
2
2
(E) √(h +s ) - h
PROPORCIONALIDADE/EQUAÇÕES 2
11. (PROFMAT-2012) A figura mostra um
pentágono regular estrelado inscrito em uma
circunferência.
O ângulo x mede:
A) 108º
B)120º
C) 136º
D)144º
E) 150º
08. (PROFMAT-2013) A figura mostra uma
Folha de papel quadrada ABCD de lado 1,
dobrada de modo que o ponto B coincida
com o ponto médio F do lado CD.
A medida de FG é
(A) 5/8
(C) 3/4
(E) 7/8
2
(B) √(h + s )
2
2
(D) √(h +4s ) - h
(B) 2/3
(D) 5/6
12. (PROFMAT-2012) Se a medida do diâmetro de
um círculo aumenta em 100%, então a medida de
sua área
aumenta em:
A) 300%
B) 100%
C) 200%
D) 400%
E) 314%
16/7/2013
3
13. (PROFMAT-2012) Na figura ao lado, o
quadrilátero grande é formado por 4
trapézios congruentes ao trapézio isósceles
sombreado.
O perímetro do quadrilátero grande é 36 cm.
Qual é o perímetro do trapézio sombreado?
A) 9 cm
B) 12 cm
C) 18 cm
D) 36 cm
E) 72 cm
16.(PROFMAT-2012)
Na figura ao lado, os hexágonos regulares
ABCDEF e A`B`C`D`E`F` estão, respectivamente,
inscrito e circunscrito à uma
circunferência de centro O.
A razão área(A`B`C`D`E`F``) ⁄ área(ABCDEF`)
vale:
PROPORCIONALIDADE/EQUAÇÕES 14. (PROFMAT-2012)
Na figura ao lado os segmentos AB, CD e EF são
perpendiculares à reta AE e medem,
respectivamente, 40m, 82m e 100m.
Se o segmento CE mede 27m, o comprimento do
segmento AC é:
A) 52m
B) 56m
C) 60m
D) 63m
E) 66m
A) 3 ⁄ 2
B) 4/3
C) √2
D) √3
*
E) 2
15. (PROFMAT-2012)
Na figura ao lado, ABC é um triângulo equilátero, M
é o ponto médio do lado AB, o segmento MN é
perpendicular ao lado BC e o segmento NP é
perpendicular ao lado AC. Sabendo que AP 12
unidades, a medida do lado do triângulo ABC nessa
mesma unidade é:
A) 15,2
B) 16,4
C) 17,5
D) 18,6
E) 19,2
16/7/2013
17. (PROFMAT-2012)
Pedro recorta em uma folha de papel um setor
º.
circular OAB de raio 12cm e ângulo de 120
Juntando e colando os raios OA e OB ele faz um
cone como mostra a figura abaixo.
4
A altura desse cone é, aproximadamente:
A) 9,6cm
20.( PROFMAT-2011) A base AB do triângulo ABC mede 8cm e está situada sobre a reta r. O segmento DE, também sobre r, mede 5cm. Pelos pontos D e E traçamos paralelas a AC e a BC respectivamente, as quais se cortam no ponto F formando o triângulo DEF. A razão área(ABC)/área(DEF) vale: (A) 1,25 (B) 1,60 (C) 3,20 (D) 2,32 (E) 2,56* B) 10,4cm
C) 10,8cm
D) 11,3cm *
E) 11,7cm
PROPORCIONALIDADE/EQUAÇÕES 18. (PROFMAT-2012)
Observe o desenho ao lado com as quatro
circunferências de raio 1 dentro da
circunferência de raio 2. A área sombreada é
igual a:
21.( PROFMAT-2011) Se espremermos um círculo de raio 10 cm entre duas retas paralelas que distam entre si 10 cm, obteremos uma figura de área menor, mas de mesmo perímetro que o círculo original. A) 2π-2
B) π/3
*
C) 2π-4
D) π /2
E) π-√π
19.( PROFMAT-2011) Na figura ao lado, as retas r
e s são paralelas a uma distância 2 uma da outra.
AB é um segmento unitário contido em s, X é um
ponto de r com AX = 5 e P é o pé da perpendicular
baixada de B sobre AX.
O comprimento de BP é:
(A) 2/3
(B) 1/5
(C) 2/5
(D) 3/4
(E) 2/3
16/7/2013
Se as partes curvas desta figura obtida são semicircunferências, a razão da área da figura espremida pela área do círculo inicial é: (A) 3/4 (B) 4/3 (C) 2/3 (D) 3/2 (E) π/4
5
22.( PROFMAT-2011) Um terreno triangular foi dividido em três terrenos menores conforme a figura. Então: (A) A área do terreno B é a metade da área do terreno A (B) A área do terreno C é maior do que a área do terreno A (C) A área do terreno B é 1/3 da área do terreno A (D) A área do terreno A é igual à área do terreno C (E) A área do terreno B é maior do que a área do PROPORCIONALIDADE/EQUAÇÕES terreno A
16/7/2013
6