2 – Contextualização química

Contextualização química
2 – Contextualização química
5
Contextualização química
2.1 – Um pouco de história acerca da espectroscopia
A radiação emitida pelo Sol, desde cedo suscitou curiosidade ao homem. Na
antiguidade já se suspeitava que essa radiação se podia decompor nas cores do arcoíris. No entanto, foi apenas no século XVII, que Newton descobriu a explicação de tal
facto fazendo passar por um prisma de vidro, um raio de luz branca, emergindo desse
prisma um conjunto de radiações coloridas, que varia do vermelho numa extremidade,
ao violeta, na outra. A esse conjunto foi dado o nome de espectro visível da luz solar.
Fig.1 Luz branca a atravessar um prisma de vidro (MARTÌNEZ, 200?)
Para além da radiação visível emitida pelo Sol, este emite ainda radiações
invisíveis ao olho humano. Foi em 1777, que o químico sueco Carl Sheele, colocou
uma amostra de cloreto de prata em cada uma das regiões coloridas do espectro
visível da luz solar. O cloreto de prata, é um sólido branco que, por acção da luz solar
se transforma em prata sólida, modificando-se assim a cor inicial. A amostra de cloreto
de prata colocada na região violeta do espectro escureceu mais rapidamente que as
restantes amostras, ou seja a reacção química que aí ocorreu foi a mais rápida. Assim
concluiu, que a radiação violeta era a mais energética do espectro visível. Em 1801, o
alemão Johann Ritter, colocou uma amostra de cloreto de prata na região escura além
do violeta tendo sido essa reacção ainda mais acelerada que as reacções até então
testadas. Assim, chegou-se à conclusão que existia uma radiação emitida pelo Sol,
mais energética que a radiação violeta, invisível aos nossos olhos a que se chamou
ultravioleta (FILGUEIRAS, 1996).
Em 1800, o astrónomo inglês William Herschel colocou um termómetro em
cada uma das regiões coloridas do espectro visível da luz solar e verificou que a
temperatura era maior na região vermelha do espectro. Ao testar a região escura além
do vermelho, Herschel observou que a temperatura era ainda maior que na região
6
Contextualização química
vermelha do espectro. Assim se descobriu a existência de outra radiação invisível aos
nossos olhos, a que foi dada o nome de infravermelho (FILGUEIRAS, 1996).
A radiação ultravioleta é uma radiação muito energética capaz de provocar
reacções químicas, enquanto que a radiação infravermelha é uma radiação de baixa
energia, suficiente para provocar o movimento de partículas constituintes de
substâncias mas insuficiente para provocar reacções químicas.
Em 1814, Joseph Fraunhofer, construtor de instrumentos ópticos, fez uma
análise pormenorizada do espectro visível da radiação solar e constatou que aí
existiam centenas de linhas negras sobre as cores. Entre a região do vermelho e do
violeta, Fraunhofer identificou 574 linhas, tendo também identificado linhas negras nas
regiões do ultravioleta e infravermelho. Com o passar do tempo, verificou-se que o
número de linhas negras era bem maior, chegando a vários milhares.
Fig.2 Espectro visível da radiação solar (HIGH R. S. SPECTRUM)
Desde há muitos séculos que se observa que alguns materiais emitem luz
quando sujeitos a temperaturas elevadas. Por exemplo, o cloreto de sódio (sal das
cozinhas) quando cai sobre a chama do gás de um fogão, esta fica amarela.
Fraunhofer constatou que ao passar por um prisma a luz emitida por esses materiais,
se obtinha um espectro discreto, com riscas coloridas sobre um fundo negro –
espectro descontínuo de emissão - e não um espectro como o da radiação solar –
espectro contínuo. Essas radiações coloridas pareciam corresponder às linhas negras
existentes
no
espectro
solar.
Constatou-se
ainda
que
estrelas
diferentes
apresentavam espectros diferentes começando a suspeitar-se que o espectro de cada
7
Contextualização química
estrela poderia ser uma impressão digital dessa estrela em termos da sua composição
química.
A
B
Fig.3 A - Espectro contínuo B - Espectro descontínuo (ANTHONY, 2003)
Em 1859, o químico Robert Bunsen, inventor do bico de Bunsen e o físico
Gustav Kirchhoff criaram um espectroscópio. Este é constituído por um fio de platina
preso a um suporte que contém o composto que vai ser sujeito a elevada temperatura
através da chama do bico de bunsen. A luz da chama obtida, atravessa um tubo de
modo a ser decomposta por um prisma e através de uma luneta também existente no
espectroscópio de Bunsen e Kirchhoff, observa-se o espectro de emissão do
composto.
Fig.4 Espectroscópio de Bunsen e Kirchhoff (OKUMURA, CAVALHEIRO e NÓBREGA, 2004)
Bunsen e Kirchhoff introduziram um sal de cloreto de sódio na chama de um
bico de bunsen, e observaram o espectro obtido através do espectroscópio.
Verificaram que as linhas amarelas obtidas o espectro coincidiam com duas das linhas
negras obtidas no espectro solar analisado por Fraunhofer. Quando fizeram passar
uma luz branca através da chama emitida pelo cloreto de sódio, observaram um
espectro contínuo com as cores do arco-íris, contendo duas linhas negras muito
próximas entre si – espectro descontínuo de absorção -, na mesma posição em que se
encontravam as linhas amarelas obtidas no espectro de emissão do sódio. Verificou-
8
Contextualização química
se então que o sódio absorve precisamente as radiações que é capaz de emitir. Assim,
Kirchhoff conclui que deveria haver vapor de sódio na atmosfera solar, devido à
existência de linhas negras presentes no espectro contínuo proveniente da radiação
solar (FILGUEIRAS, 1996).
Fig.5 Espectro de absorção e de emissão, respectivamente,
de um mesmo elemento (CHINEA, 2003)
Concluiu-se então que cada elemento tem um espectro (de emissão ou de
absorção) próprio. Bunsen e Kirchhoff utilizaram a sua descoberta como instrumento
de análise química contribuindo para a descoberta de novos elementos. Em 1860 a
partir de um resíduo alcalino da água mineral produziram um espectro de emissão
com linhas azuis, não correspondentes a nenhum elemento conhecido, tendo sido
denominado por césio, do latim caesius, azul-celeste. No ano seguinte identificaram
outro elemento que produzia linhas vermelhas intensas no espectro de emissão
nomeado de rubídio, proveniente da cor de rubi.
A espectroscopia possibilitou a descoberta de inúmeros elementos químicos,
muitos deles correspondentes a espaços vazios existentes na tabela periódica que
seria publicada por Mendeleiev em 1869.
Em 1868, o astrónomo inglês Joseph Lockyer observou detalhadamente o
espectro da radiação solar tendo descoberto um novo elemento aí existente,
desconhecido ainda na Terra, que denominou hélio em homenagem ao deus grego do
Sol. Foi apenas em 1895 que esse mesmo elemento foi descoberto na Terra pelo
químico William Ramsay.
A descoberta de novos elementos químicos mostrou a importância da
espectroscopia. As riscas características dos espectros podem ser usadas em
análises químicas para identificar elementos, por exemplo, conseguem identificar-se
elementos constituintes das estrelas através do seu espectro emitido, comparando as
riscas obtidas no espectro com as riscas de espectros de emissão de elementos
conhecidos.
9
Contextualização química
2.2 – Efeito fotoeléctrico
O efeito fotoeléctrico resulta da incidência de uma radiação electromagnética
num metal, provocando a extracção de electrões desse metal, caso a energia da
radiação seja superior à energia necessária para extrair os electrões do metal. Este
efeito foi descoberto por Hertz, em 1887 mas foi apenas com a descoberta do electrão,
em 1897, que ficou clara a causa do efeito fotoeléctrico. A energia electromagnética
transportada pela luz é absorvida por alguns electrões do metal, fazendo com que
consigam fugir à barreira de potencial que os mantém presos dentro do metal
(VILLATE, 2005).
As experiências demonstraram então, que os electrões eram extraídos da
superfície de certos metais expostos à radiação, desde que esta tivesse uma
frequência mínima, dita frequência limiar. Einstein, em 1905, verificou que quando se
aumentava a intensidade da radiação incidente no metal, o número de electrões
extraídos aumentava, não acontecendo o mesmo com as energias dos electrões
ejectados. Verificou ainda que abaixo da frequência limiar, não eram ejectados
quaisquer electrões por mais intensa que fosse a luz. Assim, Einstein nesse mesmo
ano, conseguiu explicar através da teoria de Planck, o efeito fotoeléctrico (VILLATE,
2005).
O quantum
Quando as partículas que constituem um material são sujeitas a elevadas
temperaturas, emitem radiação numa larga gama de energia. A Física clássica
considerava que as partículas constituintes desses materiais podiam emitir ou
absorver qualquer quantidade de energia. No entanto Planck, em 1900, sugeriu que
essas partículas podiam absorver ou emitir energia apenas em quantidades bem
definidas. Quantum, foi o nome dado por Planck, à mais pequena quantidade de
energia que pode ser emitida ou absorvida na forma de radiação electromagnética. A
energia de um quantum de energia emitido é proporcional à frequência da radiação. A
equação que define esta relação é a seguinte:
E=hν
Eq.1
em que ν representa a frequência da radiação e h a constante de proporcionalidade
denominada por constante de Planck que tem o valor de 6,63 × 10-34 J s.
10
Contextualização química
Foi então através da teoria de Planck, que Einstein deduziu que cada fotão1
tinha de possuir uma energia dada pela equação 1. Se a energia dos fotões tiver o
mesmo valor que a energia de ligação dos electrões no metal, então a energia da
radiação será suficiente para extrair os electrões do metal. Se a energia da radiação
for mais elevada que a energia de ligação dos electrões, os electrões serão extraídos
do metal com determinada energia cinética. A equação seguinte descreve a situação
apresentada:
h ν = EC + EL
Eq.2
em que, EC, corresponde à energia cinética do electrão ejectado e EL à energia de
ligação do electrão no metal (CHANG, 1994).
Estava assim explicado que a libertação de um electrão de um metal, no efeito
fotoeléctrico, é devida à absorção de um fotão por parte de um electrão. A energia
cinética com que ficará o electrão após a sua saída do metal, corresponderá à energia
do fotão absorvido, menos a energia de ligação do electrão no metal. O número de
electrões extraídos do metal será tanto maior quanto mais intensa for a radiação e
quanto maior for a frequência da radiação (mudança de cor), maior será a energia
cinética dos electrões extraídos. Existe uma frequência mínima da radiação para que
ocorra efeito fotoeléctrico, que corresponde à energia de ligação dos electrões no
metal e será diferente para cada metal (VILLATE, 2005).
Radiação incidente
Electrões
Metal
Fig.6 Esquema simplificado do efeito fotoeléctrico (WIKIPÈDIA, 2006)
1
Einstein sugeriu que se pensasse numa radiação não como sendo uma onda, mas sim um
feixe de partículas denominadas por fotões.
11
Contextualização química
Esta explicação para o efeito fotoeléctrico, valeu a Einstein, anos mais tarde, a
atribuição do prémio Nobel da Física. Levou ainda a que se viesse a aceitar a ideia de
que a luz possui tanto propriedades corpusculares como ondulatórias surgindo assim o
conceito dualidade onda-partícula.
Para que ocorra efeito fotoeléctrico, normalmente é necessário utilizar luz
ultravioleta, para que os electrões sejam extraídos do metal. Os metais alcalinos
libertam electrões com maior facilidade, pelo que com estes metais o efeito
fotoeléctrico poderá ocorrer com luz visível.
Na figura seguinte está representado um esquema experimental do efeito
fotoeléctrico:
Luz
Electrões = Corrente
Fig.7 Esquema experimental de aplicação do efeito fotoeléctrico (PHOTOELECTRIC E.)
Este consiste num tubo de vidro no interior do qual existem dois eléctrodos,
entre os quais se aplica uma diferença de potencial. No eléctrodo positivo (ânodo)
coloca-se um pedaço do metal desejado, sendo este posteriormente irradiado com luz,
e consequentemente extraídos alguns electrões. Alguns destes terão energia
suficiente para chegar ao outro eléctrodo (cátodo). Assim, através do amperímetro,
observar-se-á a passagem de corrente eléctrica. Este efeito é usado na construção de
células fotoeléctricas, nas quais os electrões são acelerados por campos eléctricos,
dando origem a correntes eléctricas que podem accionar alarmes, motores,
campainhas, etc (PEIXOTO, 1978).
Em 1911, e até então, a humanidade nunca esteve tão próxima de ver nascer
as primeiras teorias atómicas. É de salientar que nessa época o interesse dos físicos
era o mesmo que o interesse dos químicos, uma vez que ambos estavam
12
Contextualização química
interessados na compreensão da natureza do átomo. E talvez, por este facto, o tema
abordado nesta tese, tanto se encontra explorado em disciplinas de física como de
química, apesar de na física os conceitos serem mais direccionados para a escala
macroscópica e para a escala subatómica, enquanto que a química se ocupa
tradicionalmente da escala molecular, sugerindo assim formas alternativas da
interpretação do mesmo fenómeno.
Procuravam-se, então, explicações para a origem das radiações emitidas pelos
materiais, quando sujeitos a elevadas temperaturas, e para a origem das radiações
absorvidas por esses mesmos materiais. Para isso foram sendo analisados os
espectros de emissão e de absorção desses materiais, surgindo deste modo as
primeiras teorias atómicas.
13
Contextualização química
2.3 – Das primeiras teorias atómicas à teoria de Bohr do Átomo de Hidrogénio
Leucipo e Demócrito, no séc. V a.C., defendiam que, a matéria podia ser
repetidamente dividida e no final obter-se-ia uma fracção indivisível da matéria, o
átomo, que em grego significa pequeno e indivisível. Assim, a matéria seria constituída
por átomos que se encontrariam um pouco afastados uns dos outros, sendo os
espaços entre eles vazios.
Em 1808, o químico John Dalton publicou a sua teoria atómica baseada nas
ideias de Leucipo e Demócrito. Esta teoria sugeria que toda a matéria era constituída
por átomos indivisíveis e que cada elemento seria composto por átomos de peso
característico.
Já no século XIX em 1896, com a descoberta da radioactividade por Becquerel,
a indivisibilidade do átomo foi posta em causa: levantou-se a possibilidade da
existência de outras partículas menores que os átomos - partículas subatómicas -, pois
substâncias diferentes emitiam as mesmas partículas.
A primeira partícula subatómica, o electrão, foi descoberta em 1897 por
Thomson, provando que o átomo, afinal, não era indivisível. Ele determinou que o
electrão tem carga eléctrica negativa e que a sua massa era cerca de duas mil vezes
menor que o átomo de hidrogénio, o átomo mais simples. Com base nos resultados
obtidos, Thomson criou o primeiro modelo atómico, o modelo atómico de Thomson ou
do “Pudim de Passas”. Qualquer átomo consistia num determinado número de
electrões incrustados numa “massa” de carga positiva que equilibrava as cargas
negativas, como as passas num pudim.
O modelo de Thomson foi, mais tarde, substituído pelo modelo atómico de
Rutherford ou modelo do átomo nuclear “modelo planetário”. Em 1911, Ernest
Rutherford bombardeou folhas extremamente finas de alguns metais como ouro,
platina, chumbo e prata, com átomos de hélio, designadas por partículas α. A maior
parte das partículas atravessava a folha, mas 1 em cada 8000 era deflectida em mais
de 90º.
Partícula α
Núcleo do átomo de ouro
Fig.8 Esquema representativo do bombardeamento do metal ouro por partículas α
14
Contextualização química
O facto de as partículas α atravessarem a folha era incompatível com o modelo
de Thomson. Rutherford explicou estes resultados com um novo modelo atómico. Os
electrões, carregados negativamente, giravam em torno de um núcleo, tal como os
planetas à volta do Sol. O núcleo, muito pequeno, situava-se no centro do átomo e era
constituído por protões (do grego “primeiras coisas”), partículas carregadas
positivamente de grande massa. Apesar deste modelo explicar os resultados
experimentais tinha duas falhas. Uma delas era a existência de um núcleo com
protões, sem que este se desintegrasse devido a repulsões electrónicas. Esta falha foi
eliminada com a descoberta de mais uma partícula subatómica, o neutrão, por James
Chadwick em 1932, quando bombardeou berílio com partículas α. Esta exposição
originava a libertação da nova partícula. O neutrão é uma partícula de carga nula, que
se encontra no núcleo e com aproximadamente a mesma massa do protão. São os
neutrões que mantém a coesão do núcleo. A outra falha é que, de acordo com as leis
físicas da época um átomo como o deste tipo “morreria” instantaneamente, pois os
electrões perdiam energia e cairiam no núcleo (PlEITEZ, 2003).
Rutherford, em Manchester na Inglaterra, dirigia um grupo de pesquisas em
radioisótopos de forma a produzir raios γ e β. Neste grupo encontrava-se um físico
teórico de ideias revolucionárias, Niels Bohr, vindo da Dinamarca em 1912. Nessas
pesquisas Bohr tentava encontrar uma explicação matemática para a diminuição de
velocidade das partículas α e β ao colidirem com os electrões do átomo. Passado um
ano, Bohr regressou à Dinamarca ainda para esta questão sem resposta. Na procura
da resposta Bohr chegou a uma conclusão: as leis da física clássica não eram
adequadas para explicar o comportamento e a estrutura dos átomos. Assim, em 1913,
através do estudo em pormenor do espectro do elemento mais simples, o hidrogénio,
criou um novo modelo atómico, conhecido actualmente por modelo atómico de Bohr
do átomo de hidrogénio. Esta foi uma das mais importantes descobertas da física do
século XX, cujo processo culminou com o aparecimento da mecânica quântica. Mas tal
como refere PLEITEZ (2003) “ Bohr acertou muito e por isso está na lista dos imortais
mas, como qualquer cientista, também errou”.
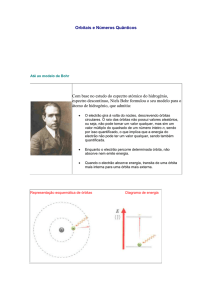
O modelo de Bohr descrevia um átomo com um núcleo formado por protões e
neutrões, e electrões que se moviam em determinadas órbitas circulares às quais
estava associada uma energia. Assim, as energias associadas ao movimento dos
electrões nas órbitas permitidas tinham um valor fixo, ou seja, eram quantificadas. No
átomo de hidrogénio, o único electrão aí existente apenas podia estar localizado em
determinadas órbitas. Assim se explicava que a emissão de radiação por esse átomo,
quando sujeito a altas temperaturas, correspondia à transição do electrão de uma
15
Contextualização química
órbita de maior energia para uma de menor energia com a formação de um quantum
de energia (fotão) na forma de luz.
Bohr mostrou que as energias que um electrão de um átomo de hidrogénio
podem assumir, são dadas por:
En =
em que RH
− RH
n2
Eq.3
tem o valor 2,18 × 10-18 J e representa a constante de Rydberg em
homenagem ao físico Robert Rydberg que estudou os espectros de riscas de vários
elementos. n pode tomar os valores 1,2,3, etc. O sinal negativo na expressão anterior,
resulta de uma convenção que estipula que a energia do electrão no átomo é mais
baixa do que a energia do electrão livre, ou seja, que está infinitamente afastado do
núcleo à qual se atribui o valor zero. Assim, à medida que o electrão se aproxima do
núcleo (n diminui), En torna-se maior em valor absoluto, mas também é mais negativo.
O valor mais negativo é atingido quando n = 1, que corresponde ao estado de menor
energia e mais estável do electrão do átomo de hidrogénio, designado por estado
fundamental. Quando n aumenta a estabilidade do electrão diminui e esses estados
são denominados estados excitados do electrão (CHANG, 1994).
Esta teoria permite explicar o espectro de riscas do átomo de hidrogénio na
medida em que cada risca no seu espectro de emissão corresponde a uma transição
do electrão. Quando um átomo passa de um estado de energia, E1, a um estado de
maior energia E2, absorve radiação de energia,
∆E = E2 – E1
Eq.4
sendo ∆E positivo. Quando um átomo passa de um estado de energia, E2, a um
estado de menor energia E1, emite radiação de energia
∆E = E1 – E2
Eq.5
sendo ∆E negativo, pois a energia é perdida para o meio circundante.
O espectro de emissão do átomo de hidrogénio abrange uma larga gama de
radiações, desde a radiação ultravioleta ao infravermelho. As radiações ultravioletas
correspondem a transições do electrão de estados excitados, para o estado
fundamental, nível 1. As radiações visíveis correspondem a transições do electrão de
estados excitados, para o nível 2. As radiações infravermelhas correspondem a
transições do electrão de estados excitados para o nível 3 ou superiores a 3. Cada
16
Contextualização química
conjunto dessas radiações constitui séries às quais foram atribuídas nomes de acordo
com os seus descobridores. Cada linha horizontal representa um nível de energia do
electrão do átomo de hidrogénio, associado a uma órbita particular.
IV
Visível
UV
Fig.9 Níveis de energia do electrão do átomo de hidrogénio
e as várias séries de emissão (MENDES e PINTO, 2003)
Foi em 1885 que Johann Balmer, professor do liceu Suíço, identificou riscas no
espectro do átomo de hidrogénio na região visível. Em 1904, Friedrich Paschen
identificou duas riscas na região infravermelha do espectro. Entre 1906 e 1924 foram
identificadas riscas na região ultravioleta por Lyman, na região infravermelha por
Brackett e Pfund (REGER, GOODE e MERCER, 1997).
No desenvolvimento desta teoria atómica, Bohr, não teve em conta a teoria
electromagnética, pelo que este modelo conduziria a um átomo instável. Do ponto de
vista clássico, a rotação de um electrão à volta de um núcleo deveria produzir uma
radiação electromagnética, dando origem a uma perda de energia do electrão
suficientemente elevada. Assim o electrão do átomo de hidrogénio, ao percorrer a sua
órbita emitiria energia continuamente, acabando por colidir com o núcleo sendo
absorvido por este. Segundo Bohr, o electrão permanecia em cada uma das órbitas
sem perder energia, contornando assim o problema encontrado (PEIXOTO, 1978).
Concluindo, Niels Bohr matematizou o modelo de Rutherford combinando-o
com as ideias sobre radiação de Planck e Einstein (BUNGE, 2002).
17
Contextualização química
2.4 – O principio da incerteza de Heisenberg
Em consequência das tentativas para explicar fenómenos atómicos, tais como,
os espectros de emissão de elementos com mais do que um electrão, o aparecimento
de novas riscas no espectro de emissão do átomo de hidrogénio, observadas quando
era aplicado um campo magnético, surgiu uma nova teoria designada mecânica
quântica. A teoria de Bohr não explicava tais factos e com a descoberta da natureza
ondulatória dos electrões, surgiu outra questão não explicada pela sua teoria. Como
não se pode definir a localização específica de uma onda, uma vez que se estende no
espaço, como é que a sua posição poderia ser específica?
Dois conceitos básicos da mecânica quântica são a dualidade onda-partícula e
o princípio da incerteza, sendo este último, uma das consequências da dualidade
onda-partícula da matéria ou energia. Segundo Villate (2005), a energia é transportada
de um ponto para outro na forma de uma onda, mas é absorvida ou emitida em níveis
discretos, na forma de partículas (quanta de energia ou fotões).
Assim, devido à natureza ondulatória da matéria não é possível conhecer
simultaneamente e com exactidão a posição e o momento linear (definido como a
massa multiplicada pela velocidade) do electrão. Este é denominado o princípio da
incerteza de Heisenberg que se descreve matematicamente através da seguinte
equação:
∆x∆p ≥
h
4π
Eq.6
em que ∆x e ∆p são, respectivamente, as incertezas na medição da posição e do
momento. Analisando a equação, verifica-se que se um electrão estiver bem
localizado não há um valor exacto da velocidade, e, se tiver um valor exacto de
velocidade, não está bem localizado (BUNGE, 2002; CHANG, 1994).
A noção determinista da trajectória da Mecânica Clássica que diz que um corpo
está em cada instante foi então substituída pelo princípio da incerteza de Heisenberg,
que assenta num determinismo diferente de tipo probabilístico: num dado instante uma
partícula tem uma determinada probabilidade de se encontrar numa região espacial,
sendo apenas possível atribuir uma probabilidade à previsão da localização da
partícula (DEUS [et.al.], 1992). Assim, ao aplicar este princípio ao átomo de
hidrogénio, o seu electrão na realidade não orbita uma trajectória bem definida tal
como era descrito na teoria de Bohr. Desta forma poder-se-ia conhecer
18
Contextualização química
simultaneamente e com exactidão a posição, através do raio da órbita, e o momento
linear do electrão, a partir da sua energia cinética e desta forma não obedecia ao
princípio de Heisenberg. No entanto, tal como no modelo de Bohr, aplicando este
princípio, a energia de um electrão num átomo é quantificada.
Assim sendo, houve a necessidade, por parte dos cientistas de desenvolver
uma equação que descrevesse completamente o comportamento electrónico nos
átomos.
19
Contextualização química
yy
2.5 – A equação de Schrodinger aplicada ao átomo de hidrogénio
yy
Em 1926, Erwin Schrodinger, físico austríaco, através do uso de técnicas
matemáticas complexas e da combinação de conceitos da Física corpuscular e
ondulatória, desenvolveu uma equação, sem a qual não teríamos acesso às
explicações de vários fenómenos químicos e físicos como por exemplo a explicação
da origem das reacções químicas e das propriedades químicas da matéria.
Não se vai aqui entrar em detalhes ou apresentar a resolução da equação de
yy
Schrodinger porque seria necessário recorrer a matemática avançada e não é este o
tema principal deste trabalho. No entanto, apresentam-se os resultados, uma vez que
sem eles não seria possível compreender a estrutura electrónica dos átomos:
•
A equação inclui o comportamento corpuscular em termos de massa e o
comportamento
ondulatório
em
termos
de
função
de
onda,
representada geralmente pela letra grega Ψ (psi);
•
A função de onda depende da localização do sistema no espaço, tal
como um electrão num átomo;
•
O quadrado da função de onda, Ψ 2, dá a probabilidade de se encontrar
um electrão em qualquer ponto do espaço, estando assim de acordo
com o princípio da incerteza de Heisenberg;
•
A intensidade da luz é proporcional é ao quadrado da função de onda,
Ψ 2, ou seja, a posição mais provável de um fotão é onde a intensidade
da luz for maior;
•
Para várias ondas electrónicas num átomo, existem várias funções de
onda, sendo cada uma delas caracterizada por um conjunto de números
quânticos (ver 3.6). Estes estão relacionados com a forma e tamanho
da onda electrónica e com a localização do electrão no espaço;
•
Tal como no modelo de Bohr, a energia do electrão pode ser calculada
para cada função de onda possível, ou seja, essa energia é quantificada
(REGER, GOODE e MERCER, 1997).
yy
E assim, com o aparecimento da equação de Schrodinger iniciou-se uma nova
era da Física e da Química, a era da mecânica quântica. No entanto, quando Bohr
apresentou a sua teoria para a estrutura atómica do átomo de hidrogénio já se falava
em teoria quântica. Essa é a chamada “teoria quântica antiga” do átomo. Na realidade,
20
Contextualização química
a teoria de Bohr é apenas parcialmente quântica, já que retém as ideias clássicas de
órbita, forma, tamanho e valor exacto de energia.
yy
Após a aplicação da equação de Schrodinger ao átomo de hidrogénio, foram
especificados os estados de energia possíveis que o electrão pode ocupar bem como
a função de onda correspondente. Conhecendo esses valores foi possível construir um
novo modelo para o átomo de hidrogénio. Segundo este modelo não é possível
conhecer a posição de um electrão no átomo num dado instante, apenas há a
probabilidade de se poder encontrar um electrão numa determinada região de um
átomo.
No modelo atómico de Bohr eram admitidas órbitas para os electrões, ou seja,
era possível conhecer simultaneamente e com exactidão a posição e o momento do
yy
electrão num dado momento. Segundo Heisenberg e Schrodinger apenas existe a
probabilidade de se encontrar um electrão numa dada região do espaço atómico.
Assim deixa de se falar em órbita e passa a falar-se em orbital, podendo esta ser
considerada como a função de onda de um electrão num átomo. Dizer que um
electrão se encontra numa determinada orbital, significa que a probabilidade de
localizar o electrão no espaço é descrita pelo quadrado da função de onda associada
a essa orbital (CHANG, 1994).
Uma orbital não se consegue visualizar, embora existam várias maneiras de a
representar sendo uma delas o modelo da nuvem electrónica. Cada ponto representa
a possibilidade de aí se encontrar o electrão. Assim, o local da nuvem electrónica onde
há maior probabilidade de se encontrar o electrão é à volta do núcleo, pois é a zona
onde se encontra uma maior quantidade de pontos.
Fig.10 Representação de uma nuvem electrónica
yy
A equação de Schrodinger pode também ser aplicada em átomos
polielectrónicos apesar de serem feitas algumas aproximações do comportamento dos
electrões nesses átomos. Essas aproximações proporcionam descrições razoáveis do
21
Contextualização química
comportamento electrónico desses átomos, facto pelo que valeu a Erwin Schrodinger
a atribuição do prémio Nobel da Física em 1933.
Uma das aplicações da mecânica quântica mais surpreendente foi na
construção do microscópio de efeito túnel. O primeiro microscópio efeito túnel (STM,
scanning tunneling microscope), foi construído em 1980 por Gerd Binning e Heinrich
Rohrer dos laboratórios de investigação da IBM em Zurique, facto pelo qual estes
cientistas receberam o prémio Nobel da Física em 1986. O funcionamento do scanning
tunneling microscope consiste numa ponta de prova aguçada feita de uma material
condutor que vai percorrer a superfície do material a estudar. A imagem que se obtém
° ou seja, de uma centésima
da superfície do material atinge uma resolução de 0,01 A,
parte do diâmetro atómico. Segundo a mecânica clássica, para se conseguirem
arrancar electrões aos átomos da superfície teriam que se aplicar campos eléctricos
muito fortes, que poderiam destruir a amostra. Segundo a mecânica quântica ao
passar a ponta de prova por cima da superfície da amostra, a uma distância
suficientemente pequena, os seus electrões saltam para o instrumento de medida
existindo uma probabilidade não nula para que isso aconteça. O STM possibilita a
distinção dos tipos de átomos que constituem uma superfície e a forma como estão
ligados. Assim, este instrumento possibilita várias aplicações tecnológicas, para além
de permitir o estudo das moléculas biológicas, a observação de processos biológicos e
consequentemente o conhecimento dos processos da própria vida (DEUS [et.al.],
Tubo com eléctrodos
1992).
Controlo de tensão
Amplificador
Controlo de
distancia
Ponta
Amostra
Fonte de
tensão
Processamento
de dados
Fig.11 Esquema do STM (WIKIPÈDIA, 2006)
22
Contextualização química
2.6 – Números quânticos
Em mecânica quântica, para descrever as orbitais atómicas e caracterizar os
electrões que nelas se encontram são necessários parâmetros, chamados números
yy
quânticos. Estes números resultam da resolução da equação de Schrodinger, tal como
já foi referido anteriormente. Os números quânticos são os seguintes: número quântico
principal (n), número quântico de momento angular ou secundário (l) e número
quântico magnético (ml). Existe ainda um quarto número quântico, número quântico de
spin (ms), que descreve o comportamento específico de cada electrão e completa a
descrição dos electrões nos átomos. Foi através de experiências com espectros de
emissão de átomos de hidrogénio e sódio, que surgiu a necessidade deste quarto
número quântico para descrever completamente o comportamento de um electrão
num átomo. De seguida descrevem-se os números quânticos referidos.
Número quântico principal (n)
•
Relaciona-se com a distância média de um electrão ao núcleo, numa dada
orbital;
•
Quanto maior for o n maior é a distância média do electrão dessa orbital ao
núcleo, e portanto maior é a orbital e a sua energia e menor é a sua
estabilidade;
•
Diferentes valores de n significam diferentes valores de energia;
•
Pode assumir os valores inteiros 1, 2, 3...
•
Corresponde ao número quântico na equação 3.
Número quântico de momento angular (l)
•
Informa acerca da forma das orbitais (tipo de orbital). Podem ser do tipo s, p, d,
f...Esta letras devem-se à relação entre as riscas espectrais observadas num
espectro de emissão e aos seus estados de energia. Assim algumas são
estreitas (em inglês sharp), outras difusas (em inglês diffuse) e outras fortes
referidas como principais (em inglês principal). Assim as letras iniciais de cada
adjectivo em inglês foram atribuídas aos diferentes estados de energia;
•
Diferentes valores de l significam diferentes subníveis;
23
Contextualização química
•
Diferentes subníveis dentro do mesmo nível, podem apresentar valores
diferentes de energia;
•
Em qualquer nível, o subnível de menor energia é o l = 0 (orbital tipo s),
seguem-se l = 1 (orbital tipo p), l = 2 (orbital tipo d), l = 3 (orbital tipo f),...;
•
Os valores de l dependem do valor do número quântico principal (n). Pode
assumir os valores inteiros compreendidos entre 0 e n -1.
Número quântico magnético (ml)
•
Descreve a orientação da orbital no espaço;
Exemplo: As orbitais do tipo p orientam-se segundo os três eixos x, y, z.
•
Especifica a orbital na qual o electrão está localizado dentro de um subnível;
•
Diferentes valores de ml significam pequenas diferenças nas energias do
electrão;
•
O número de valores de ml indica o número de orbitais num subnível com um
determinado valor de l;
•
Os valores de ml são os números inteiros de -l a +l, havendo assim, para cada
valor de l (2l + 1) valores inteiros de ml.
Por exemplo, se n = 2 e l = 1 significa que se está perante o subnível 2p.
Dentro deste subnível existem três orbitais 2p uma vez que ml pode ter os valores -1,
0 e 1. Essas orbitais são designadas por 2px, 2py e 2pz. As letras em índice indicam os
eixos segundo os quais as orbitais estão orientadas.
Número quântico de spin (ms)
•
Relaciona-se com o sentido de rotação do electrão;
•
Dado que existem dois modos de rotação do electrão, existem dois estados de
spin;
•
Pode apenas assumir os valores, + ½ e - ½.
A existência de spin electrónico foi descoberta em 1924, através de
experiências realizadas por Otto Stern e por Walther Gerlach. A experiência consistiu
na passagem de um feixe de átomos de hidrogénio por um campo magnético não
24
Contextualização química
homogéneo, sendo estes deflectidos devido à interacção com o campo magnético.
Metade dos átomos é desviada para um lado e a outra metade para outro, devido aos
movimentos
de
spin serem
completamente
aleatórios
(Chang,
1994). Este
comportamento magnético deve-se ao facto de se visualizar o electrão como uma
esfera e admitindo que lhe é permitido rodar no sentido dos ponteiros do relógio ou no
sentido inverso (REGER, GOODE e MERCER, 1997).
Resumindo, são necessários quatro números quânticos para descrever a
localização de um electrão num átomo. Cada um desses números quânticos fornece
informação acerca da provável localização do electrão no espaço atómico ou sobre o
comportamento magnético do electrão.
25
Contextualização química
2.7 – Representação e energia das orbitais atómicas
Devido ao facto das orbitais se estenderem desde o núcleo até ao infinito, não
têm formas bem definidas, não sendo possível a sua visualização. Por isso, existem
algumas maneiras de as representar que se apresentam de seguida. Existe a
probabilidade de se encontrar um electrão numa qualquer região espacial do átomo,
no entanto quase sempre se encontra perto do núcleo.
Orbitais s
A orbital s (l = 0) é representada através de uma esfera. Dentro dessa esfera
existe 90 % de probabilidade de encontrar o electrão. No entanto, onde há maior
probabilidade de se encontrar o electrão é à volta do núcleo. Todas as orbitais s têm
forma esférica mas diferem no tamanho, que aumenta à medida que aumenta o
número quântico principal.
Fig.12 Formas das orbitais 1s, 2s e 3s do hidrogénio (TEACHERS I. E. R.)
Orbitais p
As orbitais p (l = 1) têm uma forma diferente das orbitais s. Têm dois lóbulos,
um em cada lado do núcleo. Tal como nas orbitais s, nas orbitais p, dentro dos lóbulos,
existe 90 % de probabilidade de encontrar o electrão. Estas orbitais também diferem
no tamanho, que aumenta à medida que aumenta o número quântico principal, ou seja,
no sentido das orbitais 2p para as 3p, 4p e assim sucessivamente.
Se o número quântico principal (n) for igual a 1, então o número quântico de
momento angular (l) apenas poderá assumir o valor zero, pelo que existirá apenas
uma orbital 1s. No caso de n igual a 2, l já poderá tomar o valor 1. Assim ml pode ter
os valores -1, 0 e 1, existindo portanto três orbitais 2p. São elas as orbitais 2px, 2py e
26
Contextualização química
2pz todas elas idênticas na dimensão, forma e energia, diferindo apenas nas suas
orientações. Assim, só existem orbitais p a partir do número quântico principal n = 2.
Fig.13 Formas das orbitais 2p (BLABER, 1996)
Orbitais d
Quatro das orbitais d, têm a mesma forma, com quatro lóbulos idênticos que
apontam para os vértices de um quadrado. São elas as orbitais dxy, dxz, dyz e dx2–
2
y .
A
outra orbital d, dz2, tem aspecto diferente, mas é matematicamente equivalente às
outras quatro. Estas orbitais, tal como as s e as p, também diferem no tamanho, que
aumenta à medida que aumenta o número quântico principal
Só existem orbitais d a partir do número quântico principal n = 3, pois l poderá
tomar o valor 2 e assim há cinco valores possíveis para ml, que correspondem a cinco
orbitais d, que tal como as orbitais p, todas elas idênticas na dimensão, forma e
energia.
Fig.14 Formas das orbitais 3d (BLABER, 1996)
27
Contextualização química
As orbitais f são difíceis de representar, existindo em cada subnível 7 orbitais f.
Na tabela seguinte encontra-se a relação entre os números quânticos e as
orbitais atómicas.
Número de orbitais
n
l
ml
1
0
0
1
0
0
1
2
3
…
1
-1,0,1
3
0
0
1
1
-1,0,1
3
2
-2,-1,0,1,2
5
…
…
…
1
Designação das orbitais
1s
2s
4
2px, 2py, 2pz
3s
9
3px, 3py, 3pz
3dxy, 3dxz, 3dyz, 3dx2– y2
…
…
Tabela 1. Relação entre os números quânticos e as orbitais atómicas
Para além da descrição e representação das orbitais, também as suas energias
relativas fornecem informações acerca do arranjo dos electrões nos átomos.
Através da equação 3, é possível calcular a energia de um electrão num átomo
de hidrogénio, substituindo na equação o número quântico principal. A orbita 1s
corresponde ao estado mais estável do electrão, ou seja, o electrão encontra-se no
estado fundamental estando aí mais fortemente ligado ao núcleo. Se o electrão se
encontrar nas orbitais 2s, 2p, etc, diz-se que o electrão se encontra em estados
excitados.
Enquanto que no átomo de hidrogénio a energia do electrão depende apenas
do número quântico principal, num átomo polielectrónico, a energia do electrão
depende também do número quântico de momento angular. Na figura encontram-se
as orbitais de um átomo polielectrónico por ordem crescente da sua energia.
28
Contextualização química
Energia
4p
3d
4s
3p
3s
2p
2s
1s
Fig.15 Diagramas dos níveis energéticos das orbitais num átomo polielectrónico
As separações de energia entre as orbitais diminuem à medida que n aumenta,
pelo facto da energia do electrão ser inversamente proporcional a n2 (equação 3).
29
Contextualização química
2.8 – Configuração electrónica
A configuração electrónica de um átomo descreve a forma como os electrões
estão distribuídos pelas várias orbitais atómicas. A escrita da configuração electrónica
do estado fundamental dos átomos, obedece a regras. Uma delas é o princípio da
energia mínima que diz que os electrões devem ocupar as orbitais por ordem
crescente da sua energia até todas as orbitais estarem completas. Essa ordem nem
sempre corresponde à ordem crescente dos números quânticos principal e número
quântico de momento angular. Como a energia total de um átomo depende do
somatório das energias das orbitais e das repulsões entre os electrões nessas orbitais,
podem ocorrer inversões na ordem de preenchimento. Isto é, a energia total de um
átomo é inferior quando a orbital 4s é preenchida antes da orbital 3d, pois quando se
adicionam electrões ao mesmo subnível de energia, geram-se repulsões electrónicas,
que acabam por alterar a energia das orbitais. Assim, em vez de ocuparem primeiro a
orbital 3d, os electrões ocupam a orbital 4s. Ocorrem inversões deste tipo em outros
subníveis de energia, pelo que se podem usar alguns esquemas empíricos, para
preencher de forma correcta as orbitais por ordem crescente da sua energia.
Um esquema que pode ser usado tem em conta o uso de duas regras simples,
que envolvem os valores dos números quânticos n e l. A primeira refere que a energia
das orbitais aumenta à medida que aumenta a soma (n+l). Quando duas orbitais têm o
mesmo valor da soma (n+l), a orbital de maior energia será aquela que tiver maior n,
sendo esta a segunda regra. Na tabela seguinte exemplifica-se o que foi descrito:
n
l
(n+l)
Orbital
1
0
1
1s
2
0
2
2s
2
1
3
0
3
1
4
0
3
2
4
1
5
0
3
4
2p
3s
3p
4s
3d
5
4p
5s
Tabela 2. Ordem pela qual devem ser preenchidas as orbitais num átomo polielectrónico
30
Contextualização química
Outro esquema que pode ser utilizado implica escrever todas as orbitais de um
nível principal em linhas sucessivas. Nas linhas horizontais, escrevem-se as orbitais
por ordem crescente do seu número quântico de momento angular. As setas na
diagonal, apontadas para baixo e para a esquerda, indicam a ordem correcta para a
energia crescente das orbitais. Este é o diagrama de Pauling (REGER, GOODE e
MERCER, 1997).
Fig.16 Diagrama de Pauling (ATOMIC STRUCTURE)
Para além do principio da energia mínima, usado no preenchimento electrónico
das orbitas atómicas tem-se ainda em conta o princípio da exclusão de Pauli, físico
Austríaco. Foi um dos fundadores da mecânica quântica pelo que em 1945 recebeu o
prémio Nobel da Física. Segundo este princípio, num átomo não podem existir dois
electrões com os quatro números quânticos iguais, ou seja, apenas dois electrões
podem existir na mesma orbital atómica e estes têm de ter números quânticos de spin
opostos. Este princípio equivale, na mecânica quântica, dizer que dois objectos não
podem ocupar o mesmo espaço ao mesmo tempo.
Este princípio foi testado através do estudo dos electrões do átomo de hélio. Se
os dois electrões desse átomo, localizados na orbital 1s, tivessem spins iguais, ou
paralelos (↑↑ ou ↓↓), os seus campos magnéticos reforçar-se-iam tornando o átomo
de hélio paramagnético, sendo assim atraído por um íman. Se os electrões do átomo
estiverem antiparalelos entre si (↑↓ ou ↓↑), os efeitos magnéticos anulam-se tornando
o átomo diamagnético, sendo repelido por um íman. Experimentalmente verificou-se
que o átomo de hélio é diamagnético no estado fundamental, de acordo com o
princípio da exclusão de Pauli.
31
Contextualização química
Para além dos dois princípios já referidos, há ainda que ter em conta a regra de
Hund, físico alemão, no preenchimento das orbitais atómicas. Segundo esta regra, no
preenchimento de subníveis com igual energia distribui-se primeiro um electrão por
cada orbital (electrão desemparelhado) de números quânticos magnéticos diferentes,
de modo a ficarem com o mesmo número quântico de spin e só depois se completam
as restantes orbitais com o outro electrão de spin oposto. Significa que o arranjo mais
estável dos electrões em subníveis é aquele que contém o maior número de spins
paralelos.
Os esquemas seguintes mostram as diferentes maneiras de distribuir dois
electrões pelas três orbitais p.
↑↓
2px
2py
2pz
↑
↓
2px
2py
2pz
↑
↑
2px
2py
2pz
Fig.17 Esquemas de preenchimento das orbitais p
No primeiro esquema os dois electrões estão na orbital 2px, ocorrendo uma
maior repulsão entre eles do que nos segundo e terceiro esquemas que se encontram
em orbitais diferentes, 2px, 2py. O esquema que representa a forma correcta de
preenchimento de dois electrões nas orbitais p, é o terceiro pois está de acordo com a
regra de Hund (CHANG, 1994).
Para representar a configuração electrónica de um determinado elemento,
escreve-se a simbologia de cada orbital pela ordem crescente da sua energia e o
número de electrões existente em cada orbital em expoente do lado direito. Apresentase de seguida a configuração electrónica do átomo de sódio, no estado fundamental.
O número atómico desse átomo é 11, logo tem 11 electrões.
11Na
- 1s2 2s2 2px2 2py2 2pz2 3s1
A forma simplificada dessa configuração é a seguinte:
11Na
- 1s2 2s2 2p6 3s1
Através da configuração electrónica podem-se identificar os números quânticos
que caracterizam os electrões. Na tabela seguinte encontram-se representados os
números quânticos que caracterizam os electrões do átomo de sódio.
32
Contextualização química
Orbital n
l
ml
ms
Números quânticos dos electrões
1s2
1
0
0
±½
(1,0,0,±½)
2s2
2
0
0
±½
(2,0,0,±½)
6
2
1
-1; 0; +1
±½
(2,1,-1,±½); (2,1,0,±½); (2,1,1,±½)
1
3
0
0
+½ ou -½
(3,0,0,+½) ou (3,0,0,-½)
2p
3s
Tabela 3. Números quânticos que caracterizam os electrões do átomo de sódio
Na figura seguinte encontram-se as configurações electrónicas de alguns
elementos.
Hidrogénio
Hélio
Lítio
Berílio
Boro
Carbono
Azoto
Oxigénio
Flúor
Néon
Sódio
Magnésio
Alumínio
Silício
Fósforo
Enxofre
Cloro
Árgon
Potássio
Cálcio
Escândio
Titânio
Vanádio
Crómio
Manganésio
Fig.18 Configuração electrónica dos primeiros 25 elementos da Tabela Periódica
33
Contextualização química
À excepção das configurações dos átomos de hidrogénio e hélio, as
configurações dos outros elementos podem ser representadas apresentando entre
parênteses rectos o elemento gás nobre que precede, sendo aquele que mais perto se
encontre do elemento considerado, seguido pelos símbolos correspondentes aos
subníveis preenchidos mais externos. Chama-se a esta representação cerne de gás
nobre.
34
Contextualização química
2.9 – Contradições da mecânica quântica
A primeira manifestação revolucionária da mecânica quântica ocorreu em 1900,
quando Max Planck publicou um artigo em que descrevia correctamente a distribuição
de frequências da radiação emitida por sólidos em equilíbrio térmico, ou seja, quando
propôs a hipótese da quantificação energética (MAGALHÃES, 2002).
Outros cientistas questionaram a veracidade da teoria, entre eles Einstein, que
concluiu que a impossibilidade da mecânica quântica em fazer previsões unívocas, ou
seja, com probabilidade igual a um, levava a que se tratasse de uma teoria incompleta.
Em 1935, Einstein, contrariando Bohr, mostrou que a impossibilidade de se medir
simultaneamente a posição e o momento linear de uma partícula entrava, em
determinadas circunstâncias em conflito com a teoria da relatividade, não sendo no
entanto esta contradição evidente. Segundo Einstein, com a mecânica quântica seria
possível transmitir informação entre sistemas com velocidade superior à da luz, no
entanto tal ainda não foi conseguido (DEUS [et.al.], 1992).
Ainda em 1935, num debate entre Einstein e Bohr acerca da interpretação da
mecânica quântica foram discutidas as seguintes questões:
•
As teorias físicas devem representar a realidade tal como ela é,
independentemente do investigador?
•
A teoria quântica é essencialmente completa?
•
A teoria deve ser complementada com a adição de variáveis escondidas?
Einstein respondeu afirmativamente às primeira e terceira perguntas, tenho
Bohr
respondido
negativamente
a
essas
duas.
Bohr
apenas
respondeu
afirmativamente à segunda pergunta tendo sido essa contrariada por Einstein. No final
do debate as opiniões recolhidas mostraram que Bohr terá ganho o debate. Em 1951,
apenas um grupo de investigadores, entre os quais, David Bohm e Louis de Broglie,
considerou que Bohr estava errado e divulgou a teoria completa sugerida por Einstein
(BUNGE, 2002).
Segundo BUNGE, quer Bohr ou Einstein teriam fornecido ideias correctas
acerca da teoria quântica, no entanto também as teriam fornecido incorrectas e estas
em maior grau. Para o autor referido Bohr estava certo ao afirmar que a mecânica
quântica permanece verdadeira, pelo menos em parte. Estava errado ao defender que
a mecânica quântica falhava na descrição de uma realidade independente do
investigador. Einstein estava certo ao referir que todas as teorias deviam representar a
realidade o mais fielmente possível, mas estava errado ao sugerir que era necessário
tornar “mais clássica” a mecânica quântica. Ainda para o autor nem Bohr nem Einstein
35
Contextualização química
estavam correctos em relação ao carácter completo e acabado da teoria, já que
qualquer teoria empírica, embora exacta, está sempre sujeita a progressos e avanços.
A mecânica quântica, apesar de “estranhamente correcta” (MAGALHÃES,
2002), explica entre muitas coisas, a estabilidade dos átomos, a interacção entre eles
na formação das moléculas e as características das radiações que podem emitir.
Mesmo apresentando fenómenos, muitas vezes incompreensíveis, nunca explicados
pela Física clássica, tem tido dificuldades de aceitação, mesmo no meio da
comunidade científica da especialidade, sendo muitas vezes alvo de agitados debates.
No entanto, desde o “duelo científico/filosófico travado entre Bohr e Einstein no século
XX” (MAGALHÃES, 2002), esta teoria continua a ser a aceite como verdadeira até aos
dias de hoje.
E tal como disse Niels Bohr “Quem não achar a mecânica quântica estranha é
porque não a compreendeu verdadeiramente”. “É estranha mas verdadeira”
(FIOLHAIS, 1994).
36