Lista 3 - Unifal-MG

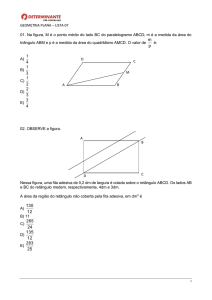
Lista 1.
1. Na figura, a área do triângulo ABC é:
2. Mostre, a partir da lei dos senos, que ângulos internos de um triângulo equilátero
circunscrito em uma circunferência de raio r, valem π/3.
3. Mostre, a partir da lei dos senos, que a soma dos ângulos internos menores de um triângulo
retângulo, circunscrito em uma circunferência de raio r, é π/2.
4. Um retângulo está circunscrito em uma circunferência de raio r. Qual o perímetro deste
retângulo se o lado maior é o dobro do lado menor?
5. Um hexágono com lados iguais está circunscrito em uma circunferência de raio r. Qual o
perímetro deste hexágono. Em relação a área da circunferência, qual a fração ocupada pelo
hexágono?
6. Obtenha
uma
expressão
que
a) cosec ( a + b ) + cosec ( a − b ) =
envolva
somente
senos
a
partir
de:
b) sec ( a + b ) + sec ( a − b ) =
7. Uma figura geométrica regular, isto é, com lados iguais, está centrada na origem do sistema
de coordenadas. A linha que liga o centro da figura com um vértice da figura e outra linha
que liga o centro a outro vértice adjacente ao primeiro definem um ângulo cujo valor é
2π/n, onde n é o número de lados da figura geométrica. Se fixarmos um vértice sobre o eixo
x, obteremos um ângulo para cada um dos vértices da figura a partir do eixo x. Se n for um
número par, qual o valor da soma dos senos destes ângulos?
8. Obtenha o valor de sen ( 4θ ) , sabendo que sen (θ ) = x .
 a+b
 a −b 
9. Transforme o sen 
 ⋅ cos 
 em uma soma de senos de a e b.
 2 
 2 