GEOMETRIA PLANA – LISTA 07 01. Na figura, M é o ponto médio

GEOMETRIA PLANA – LISTA 07
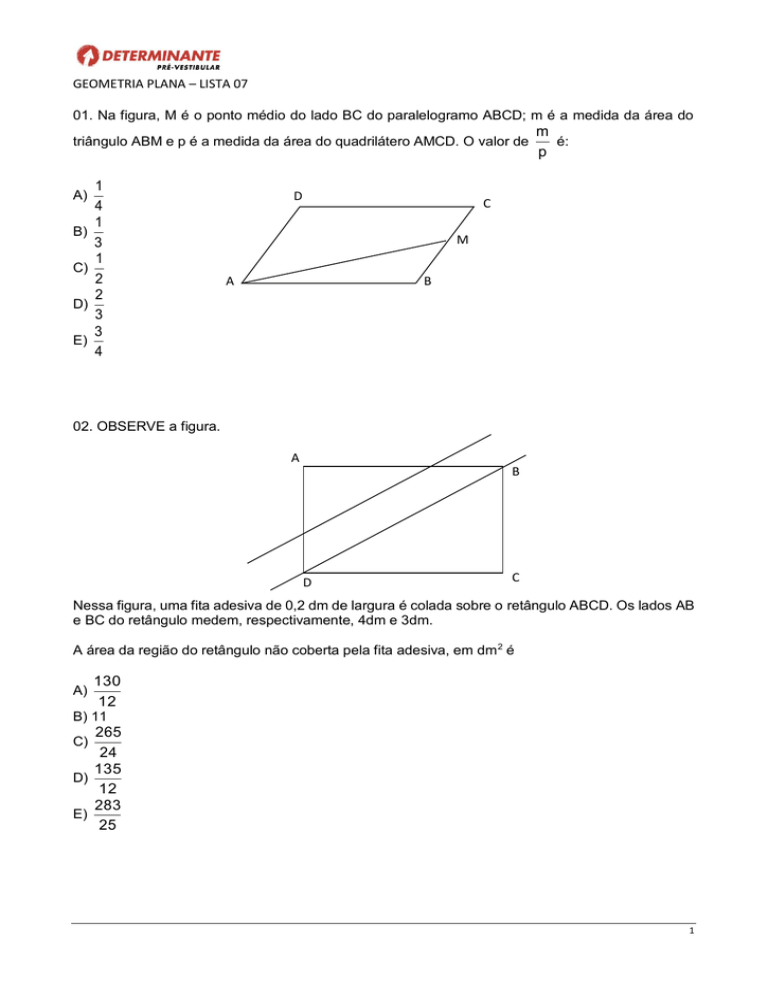
01. Na figura, M é o ponto médio do lado BC do paralelogramo ABCD; m é a medida da área do
triângulo ABM e p é a medida da área do quadrilátero AMCD. O valor de
A)
B)
C)
D)
E)
1
4
1
3
1
2
2
3
3
4
D
m
é:
p
C
M
A
B
02. OBSERVE a figura.
A
B
D
C
Nessa figura, uma fita adesiva de 0,2 dm de largura é colada sobre o retângulo ABCD. Os lados AB
e BC do retângulo medem, respectivamente, 4dm e 3dm.
A área da região do retângulo não coberta pela fita adesiva, em dm 2 é
A)
130
12
B) 11
265
24
135
D)
12
283
E)
25
C)
1
03. OBSERVE a figura.
Nessa figura, há um quadrado, uma circunferência de raio 1 e quatro triângulos equiláteros. Cada
triângulo tem um vértice na circunferência. A área da região cinza é:

A) 2 3 3  4

1 3
4
1 3
C)
2
D) 2 3  1
B)


04. Nesta figura, o triângulo equilátero ABC está inscrito numa circunferência de raio 2:
Então, a área da região hachurada é
A)
4  3 3
.
3
B)
2  3 3
.
3
C)
3  4 3
.
3
D)
3  2 3
.
3
2
05.(UFMG) Na figura, APB, AQM e MRB. São semicírculos e AM = 2MB. A razão da área hachurada
para a área do semicírculo APB é:
A)
1
3
B)
1
2
C)
2
3
D)
4
9
E)
5
9
06. OBSERVE a figura:
H
J
G
I
C
L
F
A

B
D
E
Os quadrados AFGC, CHIB e BDEA foram construídos sobre os lados do triângulo retângulo ABC.
Se a área do quadrado AFGC é 36 e sen  = 0,6, a área do retângulo BIJL é
A) 32
B) 48
C) 64
D) 82
3
07.(UFMG) Um hexágono regular de área 12 3 m2 está inscrito num círculo cujo raio mede:
A) 2m
B) 2 2 m
C) 2 3 m
D) 3m
E) 3 2 m
08. Na figura, o triângulo OPA é equilátero, a área do triângulo PAB é 2 3 e PB é perpendicular
a AB. Então, o raio da circunferência é:
O
P
A
B
A) 1
B) 4
C) 4 3
D) 8
E) 8 3
09.(UFMG) Considere NQ = MP = MN/3, sendo MN a base do retângulo KNML. Se a soma das
áreas dos outros triângulos NQL e PLM é 16. A área do retângulo KNML é:
K
L
N
Q
P
M
A) 24
B) 32
C) 48
D) 72
E) 96
4
10.(UFMG) Na figura, o hexágono regular ABCDEF está inscrito no círculo de centro O. Se
AB = 4cm, a área do quadrilátero ABOF é:
B
C
A
D
F
E
A) 8 2 cm2
B) 8 3 cm2
C) 16cm2
D) 16 2 cm2
E) 16 3 cm2
11.(UFMG) Na figura, AB é o diâmetro do círculo de centro O e C é um ponto da circunferência tal
que o ângulo A B̂ C mede 30°. Se AB = 6cm, a área da região limitada pelas cordas BC e AB e pelo
arco menor AC, em cm2, é:
A)
9 3
3

2
4
B
B) 9 3
C)
9 3
3
+
4
2
9 3
 6
D)
4
E)
Ox
C
A
3
4
5
12.(UFMG) Nessa figura, CM e AN são as alturas relativas aos lados AB e BC. Se AB = 8cm, CM =
4cm e
AN
8
 , pode-se afirmar que as medidas, de AN e BC, em cm, são, respectivamente:
BC
9
B
24
A)
e 10
5
B)
16
e6
3
M
N
C) 8 e 9
D) 10 e 6
E) 12 e 10
A
C
13.(UFMG) Nessa figura, o raio de cada um dos arcos circulares que formam as três pétalas é o
mesmo da circunferência que contém as pontas exteriores de todas as pétalas. Esse raio é igual a
20cm. A área da flor, em cm2, é:


1
400   200 3
3
1
B)
400   100 3
3
A)
C)


1
400 
 400  

6 
3 


E) 100 4  3 
D) 200 2  3 3
6
GABARITO:
1. B 2. C 3. D
4. A
5. D
6. C
7. B
8. B
9. C
10. B 11. C 12. B 13. D
7