Capítulo 1 Solução numérica de sistemas de equações lineares

Capítulo 1
Solução numérica de sistemas de
equações lineares
1.1
Introdução
O cálculo da solução de muitos problemas matemáticos é determinado pela solução de
sistemas lineares de equações. A seguir apresentamos uma breve recordação de alguns
conceitos básicos de sistemas lineares.
1.1.1
Representação matricial de sistemas de equações lineares
Sistemas de equações lineares são representados de forma matricial. Vejamos alguns exemplos. A expressão (1.1.1) representa um sistema linear de 2 equações com 2 incógnitas, x
e y:

x + 0.98y = 4.95
(1.1.1)
x + y
= 5.0
Cuja representação matricial é dada por (1.1.2):
�
1 0.98
1 1
��
x
y
1
�
=
�
4.95
5
�
(1.1.2)
Um exemplo de sistema linear de 3 equações com 3 incógnitas, x1 , x2 e x3 é dado em
(1.1.3):



= 5,
5x + x2 + x3

 1
(1.1.3)
3x1 + 4x2 + x3
= 6,



3x + 3x + 6x = 0,
1
2
3
com representação matricial dada em (1.1.4).

  

5 1 1
5
x1

  

 3 4 1   x2  =  6 
x3
3 3 6
0
(1.1.4)
Em geral, um sistema de n equações lineares com n incógnitas é escrita do seguinte
modo:









a11 a12
a21 a22
a31 a32
..
..
.
.
an1 an2
···
···
···
a1n
a2n
a3n
..
.
···
ann
↓
A
 
















x1
x2
x3
..
.
xn
↓
x










 = 






=
b1
b2
b3
..
.
bn
↓
b









Onde:
• A matriz A é chamada de matriz dos coeficientes;
• O vetor x de vetor das incógnitas;
• O vetor b de vetor dos termos independentes.
As matrizes dos coeficientes apresentadas acima são matrizes quadradas, isto é, matrizes
onde o número de linhas é igual ao número de colunas. Outros exemplos de matrizes
quadradas são mostradas abaixo:
1. Matrizes de ordem 2 (2x2)
A=
�
−1 2
2 4
�
B=
�
0 0
0 0
�
C=
�
1 0
0 1
�
2. Matrizes de ordem 3 (3x3)

−1

A= 2
3
0.001
4
45

100

0 
29

0

B= 0
0

0

0 
0
0
0
0

1

C= 0
0
0
1
0

0

0 
1
Algumas destas matrizes recebem nomes especiais.
1. Matriz identidade de ordem n ( ou nxn)

1 0 ···

 0 1


 0
I=
 ..
 .



0 0 ···
0 0
0
..
.










0 

0 1
2. Matriz quadrada A simétrica se aij = aji para todo i, j ∈ {1, 2, 3, . . . , n} .
Exemplo 1. As seguintes matrizes quadradas A e B são simétricas e de ordem 2 e 3,
respectivamente.


2 −1 30
−1 2


A=(
)
B =  −1 0 9 
2 300
30 9 4
1.1.2
Métodos numéricos para solução de sistemas lineares
Estudaremos dois métodos de solução de sistemas lineares de equações:
1. Métodos iterativos
2. Métodos diretos
1.2
Métodos iterativos
Os métodos iterativos são aqueles que permitem obter a solução de um sistema linear com
uma dada precisão, atráves de um processo infinito convergente. Exemplos de método
iterativos são o método de Jacobi e método de Gauss-Seidel.
1.2.1
Método de Jacobi e de Gauss-Seidel
Os métodos iterativos consistem em:
1. Transformar o sistema linear de ordem n:
(1.2.1)
Ax = b
em um problema de ponto fixo “linear”, isto é, um problema da seguinte forma:
(1.2.2)
x = Bx + g
onde B é uma matriz (de ordem n) e g um vetor (de n linhas).
2. Aplicar o seguinte processo iterativo no problema do ponto fixo, Eq. (1.2.2)

x(k)
x(0)
= Bx(k−1) + g,
k = 1, 2, ...
Aproximação inicial para x
(1.2.3)
3. Caso x(0) não seja dado considera-se x(0) = 0 (vetor zero)
Seguindo-se o processo acima, Eq. (1.2.3), vamos obter uma sequência de aproximações
para x:
x(1) , x(2) , x(3) , . . .
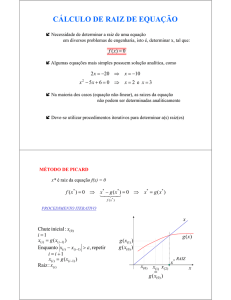
como sabemos se a sequência de aproximações {x̄(k) } converge?
Teorema 2. A condição necessária e suficiente para a convergência do processo iterativo
definido por (1.2.3) é que:
�
�
max |λi | < 1,
i=1,2,...,n
onde λi são autovalores da matriz
B (Matriz de iteração).
Corolário 3. O processo iterativo definido por (1.2.3) é convergente se, para alguma
norma de matriz, ||B|| , tem-se:
||B|| < 1
Exemplo 4. Seja:


0.5 −0.2 0.5


B =  0.1
0.6 0.4 
−0.3 0.1 0.0
Verificar se o sistema linear Ax̄ = b que tenha a matriz B acima, como matriz de iteração
convergirá para a solução.
Solução.
Lembrando: Algumas norma para matrizes B = (bij ) de ordem n, são:
�B�∞ = max
1≤i≤n
�B�1 = max
1≤j≤n
n
�
|bij | (Norma linha)
j=1
n
�
|bij | (Norma coluna)
i=1
�
��
� n 2
bij (Norma euclidiana)
�B�E = �
i,j=1
1. ||B||∞
• i = 1 : |0.5| + | − 0.2| + |0.5| = 1.2
• i = 2 :|0.1| + |0.6| + |0.4| = 1.1
• i = 3 :| − 0.3| + |0.1| + |0.0| = 0.4
• Então, ||B||∞ =1,2 > 1 Não serve.
2. ||B||1
• j = 1: |0.5| + |0.1| + | − 0.3| = 0.9
• j = 2: | − 0.2| + |0.6| + |0.1| = 0.9
• j = 3: |0.5| + |0.4| + |0.0| = 0.9
• Logo, ||B||1 = 0.9 < 1. Então, podemos afirmar que o processo iterativo com
a matriz de iteração B converge!!!
1.2.2
Processo de parada do processo iterativo
Para obtermos a solução com uma determinada precisão � devemos durante o processo
iterativo, efetuar o seguinte teste:
Se :
ER =
�
� (k+1)
�x̄
− x̄(k) �
∞
max{1, �x̄(k+1) �∞ }
< � (ER = Erro relativo)
onde � é uma precisão prefixada, x̄(k) e x̄(k+1) são duas aproximações consecutivas para x̄
(solução do sistema linear), então x̄(k+1) é a solução procurada com precisão � para x̄.
1.2.3
Método de Jacobi-Richardson
É um método iterativo para resolver sistemas lineares Ax̄ = b, onde A é uma matriz de
ordem n e b é um vetor coluna de tamanho n
a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn = b1
(e1 )
a21 x1 + a22 x2 + a23 x3 + · · · + a2n xn = b2
(e2 )
a31 x1 + a32 x2 + a33 x3 + · · · + a3n xn = b3
..
.
..
.
(e3 )
..
.
an1 x1 + an2 x2 + an3 x3 + · · · + ann xn = bn
(en )
O método iterativo de Jacobi-Richardson é dada pelos dois seguintes passos:
1. Isola-se x1 da Eq. (e1 ), x2 da Eq. (e2 ), x3 da Eq. (e3 ) e assim sucessivamente até a
última variável xn , isolada da Eq. (en ). Vamos obter as seguintes expressões:
x1 =
b1 − a12 x2 − a13 x3 − · · · − a1n xn
a11
(�
e1 )
x2 =
b2 − a21 x1 − a23 x3 − · · · − a2n xn
a22
(�
e2 )
x3 =
b3 − a31 x1 − a32 x2 − · · · − a3n xn
a33
(�
e3 )
..
.
bn − an1 x1 − an2 x2 − · · · − an,n−1 xn−1
xn =
ann
(�
en )
2. Aplica-se o seguinte processo iterativo:
3. Define-se um chute inicial x0 para obter as novas aproximaç~oes usando o passo 2.
Exemplo 5. Aplique o método de Jacobi-Richardson para resolver o seguinte sistema
linear:
4x − y + 2z = 5
x + 5y + z = 7
−0.5x + y + 2z = 2.5
Use 4 casas decimais nas suas operações e pare quando o erro relativo seja menor que
10−1 .
Solução. Isolando x, y e z das equaç~oes 1, 2 e 3, respectivamente, temos:
x = 5+y−2z
4
y = 7−x−z
5
z = 2.5+0.25x−y
2
−→
−→
−→
x = 1, 25 + 0.25y − 0.5z
y = 1.4 − 0.2x − 0.2z
z = 1.25 + 0.25x − 0.5y
Então, a iteração do método de Jacobi é dada por:
x(k) = 1, 25 + 0.25y (k−1) − 0.5z (k−1)
y (k) = 1.4 − 0.2x(k−1) − 0.2z (k−1)
z (k) = 1.25 + 0.25x(k−1) − 0.5y (k−1)
Neste caso, vamos considerar o chute inicial igual a x̄(0) = 0, isto é:
x(0) = 0,
y (0) = 0,
e z (0) = 0
Para k = 1:
x(1) = 1.25,
y (1) = 1.4, z (1) = 1.25.


1.25


x̄(1) − x̄(0) =  1.4 
1.25
� (1)
�
�x̄ − x̄(0) �
∞
ERk=1 =
(1)
�x̄ �∞
� (1)
�
�x̄ − x̄(0) �
∞
= 1.4
ERk=1 =
Para k =2:
� (1) �
�x̄ �
�
�
� (1)
�
−x̄(0) �
�x̄
�x̄(1) �∞
∞
∞
=1
= 1.4
x(2) =
y (2) =
z (2) =
1.25 + 0.25(1.4) − 0.5(1.25) 0.9750
1.4 − 0.2(1.25) − 0.2(1.25)
0.90
1.25 + 0.25(1.25) − 0.5(1.4) 0.8625


−0.2750


x̄(2) − x̄(1) =  −0.5 
−0.3875
� (2)
�
�x̄ − x̄(1) �
∞
ERk=2 =
= 0.5
�
�
�
� (2)
−x̄(0) �
�x̄
∞
�
�
� (1) �
�x̄
�
∞
�
�
� (2) �
�x̄
�
= 0.9750
∞
= 0.5127 < 10−1 ?
Na quarta iteração a condição ERk < 10−1 é satisfeita. A solução aproximada para x̄
com erro relativo < 10−1 é


0.9862


x̄(4) =  0.9825 
0.9947
Mas o método de Jacobi não converge sempre para qualquer sistema linear de equações.
Vamos dar critérios suficientes de convergência, isto é, se acontece certas hipóteses, então
o método converge. Caso contrário, não podemos dizer nada.
Proposição 6. Seja A = (aij ) a matriz dos coeficientes do sistema linear. Então,
1. Se para cada i = 1, 2, . . . , n, temos:
n
�
|aij | < |aii |
Critério das linhas
j=1
j �= i
então, o método de Jacobi-Richardson converge.
2. Se para cada j = 1, 2, . . . , n, temos:
n
�
|aij | < |aii |
i=1
i �= j
Critério das colunas
então, o método de Jacobi-Richardson converge.
Exemplo 7. Verifique se o método de Jacobi-Richardson converge quando aplicado ao
seguinte sistema linear



=7
10x1 + 2x2 + x3


= −8
x1 + 5x2 + x5



2x + 3x + 10x = 6
1
2
3
Solução. A matriz A do sistema é:


10 2 1


A= 1 5 1 
2 3 10
(1.2.4)
Vamos aplicar a critério das linhas na matriz A:
i = 1 |2| + |1| = 0.3 < 10 ? Sim
i=2
|1| + |1| < |5| ? Sim
i=3
|2| + |3| < |10| ? Sim.
Então, o método de Jacobi aplicado ao sistema linear Ax = b, com A dado pela
expressão (1.2.4), produz uma sequência de aproximações convergente!!
Observação 8. Uma matriz A com a seguinte propriedade:
n
�
|aij | < |aii |
i=1,2,. . . ,n
j=1
j �= i
é chamada de matriz diagonal dominante.
Proposição 9. Se a matriz A é estritamente diagonal dominante, então o método de
Jacobi-Richardson converge.
Exemplo 10. A matriz A dada pela expressão (1.2.4) é estritamente diagonal dominante.
Então, o método de Jacobi-Richardson converge.
1.2.4
Método de Gauss-Seidel
Da mesma forma que no método de Jacobi, no método de Gauss-Seidel o sistema linear
Ax̄ = b é escrito na forma:
x̄ = B x̄ + g
O processo iterativo consiste em, sendo x̄(0) uma aproximação inicial, calcular x̄(1) , x̄(2) ,
x̄(3) , . . . , por:
(k)
(k)
(k)
(k)
b1 − a12 x2 − a13 x3 − a14 x4 · · · − a1n xn
(k+1)
x1
=
a11
(k+1)
(k+1)
x2
=
b2 − a21 x1
(k+1)
(k+1)
x3
=
b3 − a31 x1
(k)
(k)
(k)
− a23 x3 − a24 x4 · · · − a2n xn
a22
(k+1)
− a32 x2
(k)
(k)
− a34 x4 · · · − a3n xn
a33
..
.
(k+1)
bn − an1 x1
(k+1)
− an2 x2
(k+1)
(k+1)
− a13 x3
· · · − an,n−1 xn−1
ann
Exemplo 11. Resolver o seguinte sistema linear usando o método de Gauss-Seidel
=
x(k+1)
n
4x − y + 2z = 5
x + 5y + z = 7....(∗∗)
−0.5x + y + 2z = 2.5
até que o módulo do erro relativo seja < 10−1 .
Solução.
x = 5+y−2z
4
y = 7−x−z
5
z = 2.5+0.5x−y
2
−→
−→
−→
x = 1.25 + 0.25y − 0.5z
y = 1.4 − 0.2x − 0.2z
z = 1.25 + 0.25x − 0.5y
(e1)
(e2)
(e3)
Regra associada ao método de Gauss-Seidel aplicada as equaçãoe (e1), (e2) e (e3) são,
respectivamente:
x(k) = 1.25 + 0.25y (k−1) − 0.5z (k−1)
y (k) = 1.4 − 0.2x(k) − 0.2z (k−1)
z (k) = 1.25 + 0.25x(k) − 0.5y (k)
com
x̄(0) = (x(0) , y (0) , z (0) )t = (0, 0, 0)t
Na segunda iteração do método de Gauss-Seidel aplicado ao sistema (**), tem-se:
x̄(2)
e


1, 0938


=  0.9937 
1, 0141
ER2 = 0.1475 < 10−1
Proposição 12. (Critério das linhas para o método de Gauss-Seidel). Uma condição
suficiente para garantir a convergência do método de Gauss-Seidel, quando aplicado a um
sistema Ax̄ = b, com aii �= 0, é
n
�
|aij | < |aii |
i = 1, 2, 3, , n
j=1, j�=i
Proposição 13. (Critério de Sassenfeld) Seja
M = max βi .
i=1,2,...,n
Onde os βi , são definidos por:
�n
|a1j |
|a11 |
�
� i−1
n
�
1 �
|aij |βj +
|aij | ,
βi =
|aii | j=1
j=i+1
β1 =
j=2
i = 2, 3, . . . , n
A condição M<1 é suficiente para que as aproximações obtidas pelo método de Gauss-Seidel
convirjam para a solução do sistema linear.
Exemplo 14. Calcular os valores β1 , β2 , β3 e β4 para o sistema:
2x1 + x2 − 0.2x3 + 0.2x4 = 0.4
0.6x1 + 3x2 − 0.6x3 − 0.3x4 = 7.8
−0.1x1 − 0.2x2 + x3 − 0.2x4 = 1.0
0.4x1 + 1.2x2 + 0.8x3 + 4x4 = −10
Solução. n=4
β1 =
β2
�4
|a1j |
|1| + | − 0.2| + |0.2|
1.4
=
=
= 0.7
|a11 |
|2|
2
j=2
�
� 1
4
�
�
1
|0.6|β1 + | − 0.6| + | − 0.3|
=
|a2j |βj +
|aij | =
|a22 | j=1
3
j=3
=
0.42 + 0.9
(0.6)(0.7) + 0.9
=
= 0.44
3
3
�
� 2
4
�
�
1
1
β3 =
|a3j |βj +
|a3j | =
[|a31 |β1 + |a32 |β2 + |a34 |] =
|a33 | j=1
|a33 |
j=4
� 3
�
4
�
�
1
1
[|a41 |β1 + |a42 |β2 + |a43 |β3 ] =
|a4j |βj +
|a4j | =
β4 =
|a44 | j=1
|a
|
33
j=5