Métodos iterativos para resolução de sistemas de equações

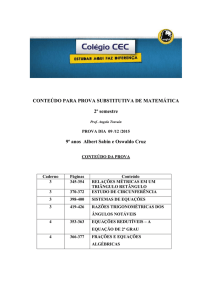
Métodos iterativos para resolução de sistemas de equações
1 Generalização do método de Newton para sistemas
O método de Newton pode ser generalizável a sistemas de equações.
E da mesma forma que o método de Newton “normal” , a sua expressão
para as iterações é obtida a partir da fórmula de Taylor truncada na
primeira ordem.
Considere-se então um sistema de 2 equações a duas incógnitas:
f1(x1,x2) = 0
f2(x1,x2) = 0
Seja x* = (x1*,x2 *) a sua solução e x(0) = (x1(0),x2(0)) uma
aproximação de x*. A partir da fórmula de Taylor temos:
∂f i
∂f
(x1(0),x2(0)) (x1*-x1(0)) + i (x1(0),x2(0)) (x2*-x2(0))
∂x 1
∂x 2
∂f
∂f1 (0)
∂f
(x(0)) x1* + 1 (x(0)) x2* (x ).x1(0) - 1 (x(0)).x2(0)
∂x 2
∂x 1
∂x 2
∂f
∂f 2 (0)
∂f
(x(0)) x1* + 2 (x(0)) x2* (x ).x1(0) - 2 (x(0)).x2(0)
∂x 2
∂x 1
∂x 2
fi(x1*,x2*) ≈ fi(x1(0),x2(0)) +
∂f1
∂x 1
∂f
0 = f2(x(0)) + 2
∂x 1
0 = f1(x(0)) +
Matricialmente vem:
em que F = f1(x(0))
0 = F(x(0)) + J(x(0)).x* - J(x(0)).x(0) ;
; J(x(0)) =
f2(x(0))
x* =
x1*
x2*
x(0) =
∂f1 (0)
(x )
∂x 1
∂f 2 (0)
(x )
∂x 1
∂f1 (0)
(x )
∂x 2
∂f 2 (0)
(x )
∂x 2
x1(0)
x2(0)
então: J(x(0)).x* = - F(x(0)) + J(x(0)).x(0) ; se J é invertível vem que
x* = x(0) - J(x(0))-1.F(x(0))
Assim sendo o método é dado por:
xm = xm-1 - J(xm-1)-1.F(xm-1)
Para se evitar o cálculo de matrizes inversas pode-se usar a expressão
alternativa:
J(xm-1).xm = J(xm-1).xm-1 - F(xm-1)
O método pode ser traduzido pelo seguinte algoritmo
1) Dado x(0) qualquer,
2) Seja m = 1,2,...,q
a) Calcular b1 = - F(xm-1),
b) Calcular J(xm-1),
c) Calcular b2 = J(xm-1).xm-1,
d) Calcular b = b1 + b2 ,
e) Resolver o sistema J(xm-1). xm = b.
O método funciona sempre para qualquer que seja a escolha de x(0),
isto é o método é sempre convergente.
2 Métodos iterativos para resolução de sistemas lineares
Considere-se um sistema Ax = b, e decomponha-se A na forma N-P
ou seja:
A = N – P;
desta forma temos que:
Nx = Px + b, se N-1 existir vem que:
x = N-1P.x + N-1b
⇔ x = M.x + d
e assim sendo podemos escrever o método iterativo por:
xm = M.xm-1 + b,
M é designada por matriz de iteração e
m
x é a iteração de ordem m.
Para que o método funcione é necessário que seja convergente. A
convergência é garantida se o raio espectral da matriz de iteração for menor
que 1, ou seja ρ(M) < 1
Nota: ρ(M) = max { |λ| : λ é valor próprio de M }
Uma forma mais expedita para se verificar a convergência é verificar
se o módulo de M é menor que 1. O módulo utilizado pode ser qualquer um
dos definidos para matrizes, dos quais dois são os seguintes:
n
||M||1 = maxj
∑
| mij |
i =1
n
||M|| ∞ = maxi
∑
j=1
| mij |
Nota: ρ(M)< 1 ⇔ método convergente (condição necessária e suficiente)
||M|| < 1 ⇒ método convergente (condição suficiente)
||M|| ≥ 1 nada se pode concluir
Como se tratam de métodos que fornecem soluções numéricas
aproximadas, estes métodos têm um erro que lhes é inerente. Uma
estimativa para o erro é aquela traduzida pela expressão seguinte:
|| M || m
Em =
. ||x(1) - x(0)|| ,
1 - || M ||
Em < δ, em que δ é o erro exacto ou seja
δ = || x – xm || .
3 Método de Jacobi
Este método engloba-se no grupo de métodos descrito na secção
anterior, em que a matriz A é decomposta em D-L-U, isto é A = D-L-U, em
que D é uma matriz diagonal, L é triangular inferior e U triangular superior.
Vem então:
Ax = b ⇔ Dx = (L+U).x + b ⇔
x = D-1 (L+U).x + D-1b
daqui vem que o método iterativo é dado por:
xm = D-1 (L+U).xm-1 + D-1b
matriz de Jacobi
M
d
3 Método de Gauss-Seidel
Neste caso A = D-L-U, tal que: Ax = b ⇔ (D-L)x = Ux +b ⇔
⇔ (I-D-1L)x = D-1Ux + D-1b ⇔ x = (I-D-1L)-1D-1Ux + (I-D-1L)-1D-1b
então:
xm = (I-D-1L)-1D-1U.xm + (I-D-1L)-1D-1b
matriz de Gauss-Seidel
M
d
(Trabalho apresentado por Daniel Covita)