Lista Lei dos Senos e Cossenos

Lei dos Senos e Cossenos – Professora Renata Fonseca
GABARITO
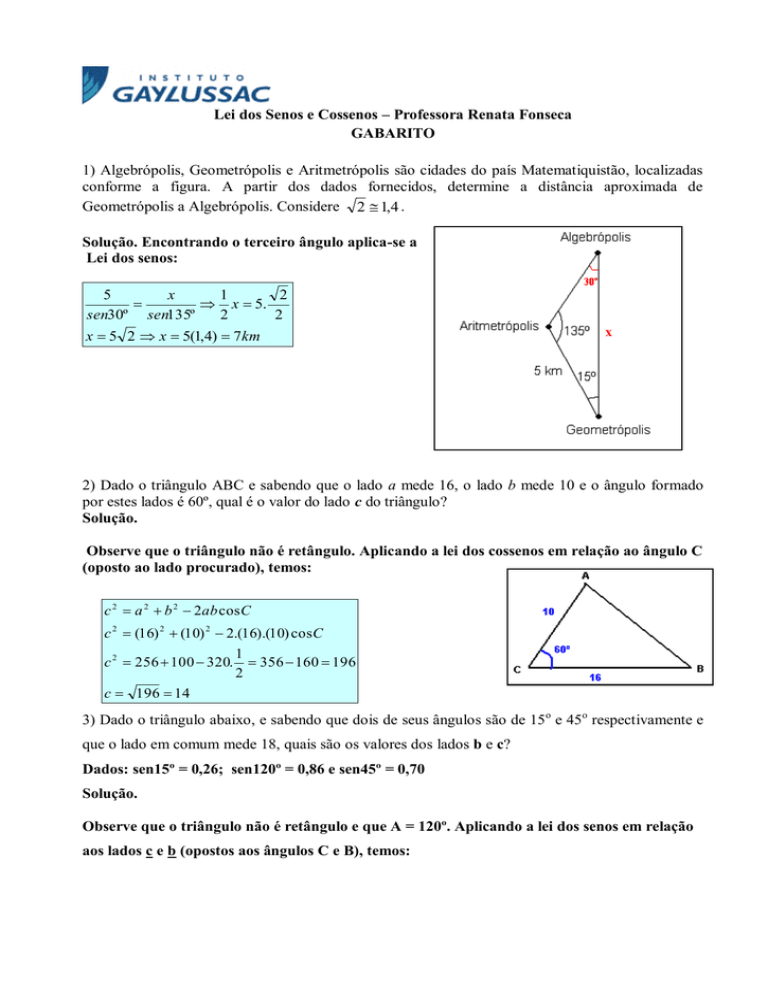
1) Algebrópolis, Geometrópolis e Aritmetrópolis são cidades do país Matematiquistão, localizadas
conforme a figura. A partir dos dados fornecidos, determine a distância aproximada de
Geometrópolis a Algebrópolis. Considere 2  1,4 .
Solução. Encontrando o terceiro ângulo aplica-se a
Lei dos senos:
5
x
1
2

 x  5.
sen30º sen135º
2
2
x  5 2  x  5(1,4)  7km
x
2) Dado o triângulo ABC e sabendo que o lado a mede 16, o lado b mede 10 e o ângulo formado
por estes lados é 60º, qual é o valor do lado c do triângulo?
Solução.
Observe que o triângulo não é retângulo. Aplicando a lei dos cossenos em relação ao ângulo C
(oposto ao lado procurado), temos:
c 2  a 2  b 2  2ab cos C
c 2  (16) 2  (10) 2  2.(16).(10) cos C
1
c 2  256  100  320.  356  160  196
2
c  196  14
3) Dado o triângulo abaixo, e sabendo que dois de seus ângulos são de 15 o e 45o respectivamente e
que o lado em comum mede 18, quais são os valores dos lados b e c?
Dados: sen15º = 0,26; sen120º = 0,86 e sen45º = 0,70
Solução.
Observe que o triângulo não é retângulo e que A = 120º. Aplicando a lei dos senos em relação
aos lados c e b (opostos aos ângulos C e B), temos:
a
b
c
18
b
c





senA senB senC
sen120º sen15º sen45º
18(0,26)
b
 5,44
0,86
18(0,70)
c
 14,65
0,86
4) No paralelogramo desenhado abaixo, obtenha a medida da diagonal maior.
Solução. Observe que a diagonal é o lado oposto ao ângulo de 120º. Aplicando a lei dos
cossenos em relação ao ângulo C (oposto à diagonal D procurada), temos:
D 2  a 2  b 2  2ab cos C
D 2  (4) 2  (3) 2  2.( 4).(3) cos C
1
D 2  16  9  24 cos C  25  24.(  )  25  12  37
2
D  37  6,08cm
5) Sabendo que em um triângulo qualquer seus lados medem respectivamente 3, 5 e 7 , qual o valor
do cosseno do ângulo C deste triângulo?
Solução. Esta situação apresenta somente lados e o ângulo procurado está oposto ao lado
medindo 5. Aplicando a lei dos cossenos em relação ao ângulo C, temos:
c 2  a 2  b 2  2ab cos C
5 2  (7) 2  (3) 2  2.(7).(3) cos C
25  49  9  42 cos C
 33
 42 cos C  25  58  cos C 
 0,79
 42
6) Um triângulo é tal que AB = 2 3 cm e AC = 6cm. Calcule a medida do lado BC sabendo que os
ângulos internos dos vértices B e C são tais que B = 2C.
Solução. O lado AC está oposto ao ângulo B. O lado AB está oposto ao ângulo C. Aplicando a
lei dos senos, temos:
6
2 3
. O termo (sen2C) pode ser desenvolvido como:

sen2C senC
2senCcosC.
Voltando ao problema, temos:
2 3 (2senC cos C )
6
2 3
6
6 3
3

6
 6  4 3 cos C  cos C 


.
sen2C senC
senC
2
4 3 4 3 3
Logo
C = 30º e B = 2C = 60º. Esse resultado indica que o terceiro ângulo vale 90º e o triângulo é
retângulo.
O
lado
 
a  62  2 3
2
BC
oposto
ao
ângulo
reto
é
hipotenusa
e
vale:
 36  12  48  4 3cm.
7) No triângulo da figura, x = 30º, y = 15º e AC mede 15 2 . Calcule o lado BC.
Solução. O ângulo B vale: 180º - (30º + 15º) = 135º. Aplicando a lei dos senos, temos:
15 2
BC
15 2
BC
15 2 BC





1
senB senx
sen135º sen30º
2
2
2
15 2.
1
2
 BC.
 BC  15.
2
2
9) Considere um triângulo cujos lados medem 5cm, 6cm e 9cm. Qual a área de um quadrado cujo
lado é a mediana relativa ao maior lado do triângulo considerado em centímetros quadrados?
Solução. Aplicando a lei dos cossenos, temos:
2
2
2
i) 6  5  9  2(5)(9) cos y  cos y 
36  106 70

 90
90
2
9
9
m  5     2(5)( ) cos y
2
2
ii)
.
81
70
2
2
2
m  25   45( )  m  10,25cm
4
90
2
2
8) Calcule o cosseno do ângulo obtuso x do triângulo ABC.
Solução. Aplicando a lei dos senos, temos:
3
4
3
4
1

 
 3senx  4.
1 senx
sen30º senx
2
2
2
2
3senx  2  senx  .  cos x  1   
3
3
cos x  1 
2
4
5
5


 (obtuso)
9
9
3
9) Calcule a soma dos lados AC e BC do triângulo.
Solução. Aplicando a lei dos senos, temos:
 
3 2
BC
3 2
4
3 2




1
sen30º sen45º
2
2
i)
2
2
32. BC
2.3.2

 BC 
6
2
2
2
2
 BC.
1
2
ii) Aplicando a lei dos cossenos em relação ao lado AB, temos:
(3 2 ) 2  BC 2  AC 2  2( BC )( AC ) cos 30º  12  36  AC 2  2(6)( AC ).
3
2
12 3
AC 
AC  18  36  0  AC 2  6 AC  18  0  AC 2  6 3 AC  18  0
2
.
2
Resolvendo:
AC 
 (6 3 )  108  4(1)(18) 6 3  36 6 3  6


 3( 3  1) . Como o ângulo
2
2
2
oposto ao lado AC é obtuso, ele é o maior lado. Logo AC = 3( 3  1). Logo a soma pedida AC
+ BC será o valor AC  BC  6  3( 3  1)  3(2,73)  6  14,2.
10) Calcule o valor de cos x no triângulo da figura.
Solução. Aplicando a lei dos cossenos, temos:
2
 3R 
2
2
2
2
2
   R  R  2( R)(R) cos x  9 R  8R  8( R ) cos x
 2 
1
R 2  8( R 2 ) cos x  cos x 
8
11) Uma certa propriedade rural tem o formato de um trapézio como na figura. As bases WZ e XY
do trapézio medem 9,4 km e 5,7 km, respectivamente, e o lado YZ margeia um rio. Se o ângulo
XYZ é o dobro do ângulo XWZ, a medida, em km, do lado YZ que fica à margem do rio é:
(A) 7,5.
(B) 5,7.
(C) 4,7.
(D) 4,3.
(E) 3,7.
Solução. Traçando uma paralela ao
lado WX, construímos um triângulo
isósceles com os dois ângulos iguais
a “b”. Logo, o lado YZ possui a
mesma medida de 3,7km do outro
lado.
12) Um topógrafo pretende medir a distância entre dois pontos (A e B) situados em margens
opostas de um rio. Para isso, ele escolheu um ponto C na margem em que está, e mediu os ângulos
ACˆ B e CAˆ B , encontrando, respectivamente, 45° e 75º.
_____
Determine AB , sabendo
(Utilize 2  1,4 ).
_____
que
AC
mede
16
m.
Solução. Aplicação da Lei dos Senos:
16
x
3
2


x  16
sen60º sen45º
2
2
16(1,4) 22,4 3 22,4 3
3 x  16 2  x 


m
3
3
3. 3
13) Calcule a distância dos pontos A e B, entre os quais há uma montanha, sabendo que suas
distâncias a um ponto fixo M são de 2km e 3km, respectivamente. A medida do ângulo AMˆ B é igual
a 60º.
Solução. Aplicação da Lei dos cossenos:
x 2  2 2  3 2  2(2)(3) cos 60 º
1
x 2  4  9  12 .
2
x 2  13  6  x  7km.