Res QA2.4

Nome _____________________________________
Professor __________________________
Nº ____
Turma: 11.º __
Data: ___/___/___ Classificação ______
Questão Aula – RELAÇÕES TRIGONOMÉTRICAS
Apresente todas as explicações de forma clara e organizada,
indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias.
(25)
1.
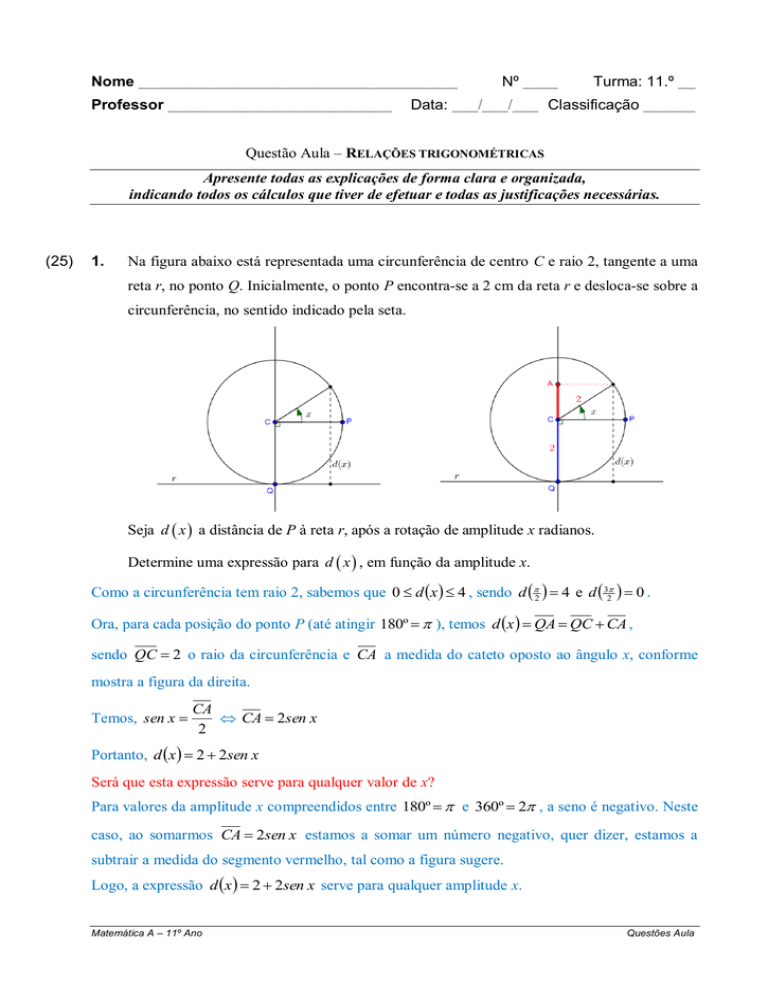
Na figura abaixo está representada uma circunferência de centro C e raio 2, tangente a uma
reta r, no ponto Q. Inicialmente, o ponto P encontra-se a 2 cm da reta r e desloca-se sobre a
circunferência, no sentido indicado pela seta.
Seja d  x  a distância de P à reta r, após a rotação de amplitude x radianos.
Determine uma expressão para d  x  , em função da amplitude x.
Como a circunferência tem raio 2, sabemos que 0  d x   4 , sendo d 2   4 e d  32   0 .
Ora, para cada posição do ponto P (até atingir 180º   ), temos d x   QA  QC  CA ,
sendo QC  2 o raio da circunferência e CA a medida do cateto oposto ao ângulo x, conforme
mostra a figura da direita.
Temos, sen x 
CA
 CA  2sen x
2
Portanto, d x   2  2sen x
Será que esta expressão serve para qualquer valor de x?
Para valores da amplitude x compreendidos entre 180º   e 360º  2 , a seno é negativo. Neste
caso, ao somarmos CA  2sen x estamos a somar um número negativo, quer dizer, estamos a
subtrair a medida do segmento vermelho, tal como a figura sugere.
Logo, a expressão d x   2  2sen x serve para qualquer amplitude x.
Matemática A – 11º Ano
Questões Aula
2.
Na figura seguinte está representado o círculo trigonométrico.
O ponto A desloca-se sobre a circunferência, no primeiro quadrante.
O ponto B é o simétrico do ponto A relativamente ao eixo Oy.
C é o ponto da circunferência que pertence ao semieixo positivo Ox.
(15)
2.1 Indique as coordenadas dos pontos A e B quando  
Como estamos no círculo trigonométrico, para  

3

3
.
as coordenadas do ponto A são

  1
3

.
 cos , sen  =  ,
3
3   2 2 

Como o ponto B é simétrico do ponto A relativamente ao eixo Oy as suas coordenadas são

   1 3 

.
  cos , sen  =   ,
3
3   2 2 

(40)
2.2 Sendo  a amplitude, em radianos, do ângulo COA, determine uma expressão para o
perímetro da região limitada pela corda BA e o arco BA (região sombreada).
Não temos um processo direto de cálculo do perímetro do segmento circular.
A alternativa é somar o comprimento do segmento BA com o comprimento do arco BA.
O comprimento de um arco de amplitude  radianos e raio r é dada por Carco     r
Neste caso, temos um ângulo de amplitude   2 e r  1 .
Assim, Ca    2   1    2
O comprimento do segmento BA é o dobro do segmento DA.
Como DA  cos  , temos BA  2 cos  .
Logo o perímetro da região sombreada é dado pela expressão C    Ca  BA    2  2 cos  .
Matemática A – 11º Ano
Questões Aula
3.
Na figura seguinte está representado um triângulo ABC, cujos ângulos têm amplitudes , 
e 2 .  é um ângulo externo do triângulo adjacente ao ângulo .
(20)
3.1. Partindo da relação entre os ângulos internos e externos de um triângulo, prove que:
cos    cos 
Como qualquer ângulo externo do triângulo é suplementar do ângulo interno adjacente, temos
   .
Portanto,      .
Assim, cos   cos    
Simplificando, temos cos    cos  c.q.m.
(30)
3.2. Admitindo que tan 2  3   3 , determine a amplitude dos ângulos  e , em radianos.
Efetuando a redução de tan 2  3   3 obtemos tan 2   3 .
Portanto, 2  tan-1 3  2 
Assim,        

6

    3 =   3
Matemática A – 11º Ano

3
 

6
5
6

6

3 

6
2
Questões Aula
4.
(30)
Considere a expressão A   
4.1. Mostre que A   
A  
2
.
tan 
1  cos    sen 2
1  cos 
sen 
=
=

sen   1  cos  
sen  1  cos 
2
1 cos  
(40)
1  cos 
sen 
, com   k , k  .

sen  1  cos 
para colocar o mesmo denominador
 sen  
=
1  2 cos   cos 2   sen 2
sen   1  cos  
calculando as potências do numerador
=
cos 2   sen 2  2 cos   cos 2   sen 2
sen   1  cos  
porque 1  sen2  cos 2 
=
2 cos  1  cos  
2 cos   2 cos 2 
=
sen   1  cos   sen   1  cos  
pondo 2cos  em evidência
=
2 cos 
sen 
“cortando” dos fatores comuns
=
2
tan 
c.q.m.
porque
cos 
1

sen  tan 
 3
 1
    e   0,   .
4.2. Determine A   , sabendo que sen 
 2
 3
Para determinar A   
2
precisamos de conhecer o valor de tan  .
tan 
 3

   , para sabermos algo sobre o ângulo .
Comecemos por simplificar a expressão sen 
 2

 3

     cos 
Temos, sen 
 2

Portanto,  cos  
De
1
1
 cos    e ficamos a saber que   2.º Q (cosseno negativo)
3
3
sen2 cos 2 
1
1


obtemos tan2   1 
que permite descobrir tan  .
2
2
2
cos  cos  cos 
cos 2 
Temos: tan 2   1 
1
 
1 2
3
 tan2   9  1  tan    8  tan   2 2
Como   2.º Q , então tan   2 2 (negativa)
Portanto, A   
Matemática A – 11º Ano
2
1
2
2
=
= 
=
tan  2 2
2
2
Questões Aula