O Limite de uma Função - Centro de Estudos Espaço

Cálculo I – Limite de uma função
Sartori, C. S.
01
Revisão - Funções:
- Definição:
Lembrando que uma função é uma relação
entre dois conjuntos que obedecem às restrições:
1) Esta relação envolve um elemento do
primeiro conjunto, chamado domínio da função f em
apenas um elemento do outro conjunto denominado
contra-domínio.
2) Uma vez definido o conjunto X (domínio)
todos elementos deste devem ser relacionados.
8
6
4
2
-3
-2
-1
1
2
3
-2
1
-4
-6
Notação:
f:X
Y
-8
I - Funções Elementares:
Classificação:
Sobrejetora: Uma função é sobrejetora,
quando seu conjunto imagem é igual ao seu contra
domínio.
Injetora: Uma função é injetora quando todos
os elementos de seu domínio possuem imagens
distintas.
{ x1,x2 Dom f(x) (x1 x2) f(x1) f(x2)}
I.a - A Função Linear:
A função linear é definida, em sua forma reduzida, por:
y = ax + b.
O valor de a é denominado de coeficiente angular e
relaciona-se com a inclinação da reta com o eixo x. Já o valor de
b é a interceção da reta com o eixo Oy, ou seja o ponto de
coordenadas (0,b). Sejam dois pontos por onde a reta passa:
P1 ( x1 , y1 ); P0 ( x0 , y0 )
Bijetora: Quando for injetora e sobrejetora.
Classificação quanto á Paridade:
y
ax b
Função Par:
a
y
x
Uma função é quando f(+x)=f(-x)
O gráfico da função par é simétrico em
relação ao eixo Oy.
-3
-2
-1
1
2
3
1
2
y0
x0
É útil também sabermos a equação do feixe de retas que
passa pelo ponto P0 ( x0 , y0 ) :
f ( x)
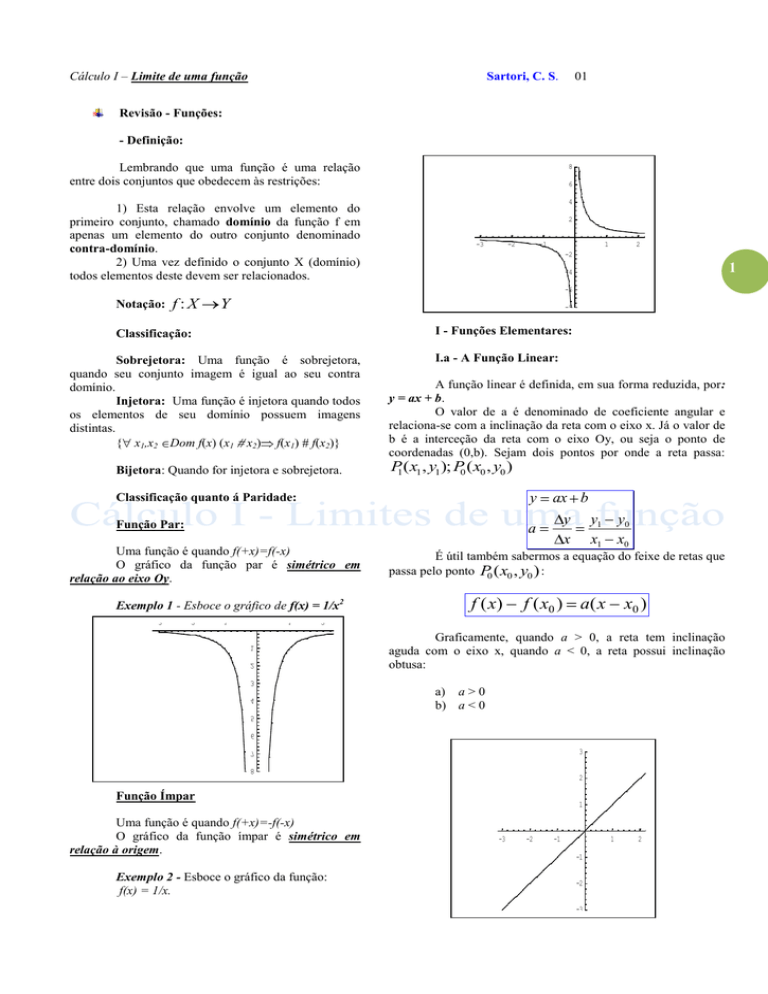
Exemplo 1 - Esboce o gráfico de f(x) = 1/x2
y1
x1
f ( x0 ) a( x
x0 )
Graficamente, quando a > 0, a reta tem inclinação
aguda com o eixo x, quando a < 0, a reta possui inclinação
obtusa:
3
4
5
a) a > 0
b) a < 0
6
7
3
8
2
Função Ímpar
Uma função é quando f(+x)=-f(-x)
O gráfico da função ímpar é simétrico em
relação à origem.
Exemplo 2 - Esboce o gráfico da função:
f(x) = 1/x.
1
-3
-2
-1
1
-1
-2
-3
2
3
Capítulo 2 - O Limite de uma função
Sartori, C. S - 2
3
2
1
-3
-2
-1
1
2
3
-1
-2
-3
Tente encontrar, a partir do gráfico, as
equações destas retas. Observe que o domínio é o
conjunto dos números reais (R) e o conjunto imagem
(Im f = R).
I.
> 0
f(x) possui 2 raízes reais e distintas.
II. = 0
f(x) possui 1 única raiz real.
III. < 0
f(x ) Nenhuma raiz real.
A função quadrática, ou parábola, poderá ter um ponto
de máximo ou de mínimo, conforme o sinal de a:
IV. a > 0
Concavidade para cima
- Ponto de
mínimo em yv.
V. a < 0
Concavidade para baixo
- Ponto de
máximo em yv.
VI. f(x) = ax2+bx+c = a(x-x1)(x-x2)
Onde x1 e x2 são raízes de f(x)
As coordenadas do vértice da parábola são dadas por:
V
4a
VI. Conjunto Imagem:
Se a > 0
Im f = [ yv , )
Se a < 0
Im f = (- , yv ]
- VII. Relação entre coeficientes e raízes: Soma e
I.b. Função módulo.
A função módulo é definida por:
y
b
; yv
2a
( xv , yv ); xv
x
x; x
0
x; x
0
a) Domínio: R; conjunto imagem: y
b) Gráfico:
Produto
[0,
).
S
x1
P
x1 . x2
:
3
2.5
b
a
x2
c
a
VIII. Gráficos:
2
a >0
>0
1.5
8
1
6
0.5
4
-3
-2
-1
1
2
3
2
-0.5
-1
-2
2
4
6
-2
i)
c) Propriedades:
x 0 x R
iii) x
a ;a
R
iv) x
a ;a
R
-4
ii) x
x
y
x
a; x
a
y
-6
a
x
-8
a <0
a
>0
8
v) x
x2
I.c - A Função Quadrática:
6
4
A função quadrática é toda expressão do tipo:
F: A
B; f ( x)
Raízes:
f ( x)
ax
2
Ao
bx c
b
x
b
2
ax2 bx c; a
2
0
-2
resolvermos a equação:
0 ; teremos como solução:
b2 4ac
2a
4ac
2
-2
-4
b
-6
2a
-8
(Equação de Báscara)
Dependendo do valor do delta teremos os
seguintes casos:
2
4
6
Capítulo 2 - O Limite de uma função
Sartori, C. S - 3
7.5
I.e - A Função logarítmica:
5
A função logarítmica é definida por :
f :( 0, ) R; y loga x
x
2.5
0
ay
Condições de Existência
:
-2.5
-5
-7.5
-4
-2
0
2
4
x 0, a 0 e a 1
Assim, temos para que a função logarítmica seja
definida, deve-se satisfazer sempre as condições de existência. x
é chamado de logaritmando e a de base.
I.d - A Função exponencial:
A função exponencial é definida
f : R R; f ( x) a x , a 0; a 1.
nida
por:
Quando a for maior que 1 , a função é crescente;
quando 0 < a < 1 a função é dita decrescente. O
Domínio da função exponencial é o conjunto dos
números reais (Dom f = R). Já o conjunto imagem é o
intervalo: {y
R
y > 0} , ou seja, a função
exponencial é extritamente positiva, tanto a crescente
como a decrescente.
I. Domínio: x
(0, )
II. Imagem: y
R.
III. Propriedades: A função logarítmica é a função
inversa da função exponencial de mesma base.
i) loga x y x a y ii) loga 1 0
iii) loga x1 loga x2 loga ( x1 . x2 )
iv) loga (
15
loga x1
vii) Se 0 < a 1 e loga x2
x2
loga x1
12.5
vii) Seja a 0, b 0 e a , b 1
10
viii) a lo ga x
7.5
a
x1
) loga x1 loga x2
x2
v) loga x n n loga x
vi) Se a 1 e loga x2
I. Gráficos:
.
logb x
x1
x2
x1
loga x
loga b
x
5
2.5
0
-4
-2
0
2
Note que a reta y = 0 nunca intercepta o
gráfico da função exponencial; ela é dita uma assíntota
à função.
II. Conjunto Imagem: {y R y > 0}
III. Domínio: x
4
iv) Gráficos:
A função logarítmica pode ser crescente
decrescente (0 < a < 1).
O gráfico abaixo ilustra cada caso.
R.
4
3
IV - Propriedades: Seja a > 0 e a 1. Sejam
R. As seguintes propriedades são válidas:
xey
x
i) a .a
y
a
ax
ii) y
a
a
v) a 0
1
x y
x y
iii) (a )
x
x y
(a > 1) ou
iv) a
a
2
x. y
1
0
y
x
a
y
-1
-2
vii) Se a
x
viii) Se a x
vi
)a
y
a ea 1
1
ax
x
x
y
a ye 0 < a 1
x
-3
0
2.5
5
7.5
10
12.5
15
Notar que a assíntota à função logarítmica é a reta x=0
y
3
Capítulo 2 - O Limite de uma função
Sartori, C. S - 4
II - Funções Trigonométricas
II.a Métricas:
a
b
c
b
a
c
a
sen
cos
tg
b
c
Então:
Triângulo Retângulo: Relações
a
c
cos
sec
sen
cos sec
1
tg
sen
sen( - )
cos
-cos ( - )
tg
- tg ( -x)
III Q
1800<
-sen ( - )
-cos ( - )
tg ( - )
< 2700
IV Q
900 <
-sen (2 - )
cos (2 - )
-tg(2 - )
< 3600
1
cos
a
1
b sen
1
tg
c
b
ctg
Quadrante:
II Q
900< < 1800
II.b) Relações Fundamentais:
sen2 x cos2 x
sec2 x
1
1 tg 2 x
cossec2 x
1 ctg 2 x
Observação:
Estudo de sinais: Círculo Trigonométrico:
cos
/2
90
II Q
2
Valores particulares:
IQ
tgx
senx

sen
2
x
cosx
180
III Q
0
sen
cos
tg
0
0
1
0
6
1
2
3
2
3
3
2
2
3
3
2
2
2
1
2
1
4
1
0

0
-1
-1
0
0

0
1
0
IV Q
3
2
3
2
3
2
270
Quadrante
0
I Q (0 < x < 90) )
2
senx
cosx
tgx
+
+
+
0
0
+
-
-
0
0
I Q (180 < x < 270 )
-
-
-
I Q (2700 < x < 3600)
-
+
-
I IQ (90 < x < 180 )
II.c) Gráficos:
IIc.1) Função seno:
1
0.5
Tabela de Conversão:
0
Seja x I quadrante e um ângulo qualquer:
Podemos encontrar as funções trigonométricas
desse ângulo a partir do correspondente ângulo do
primeiro quadrante, fazendo a chamada conversão ao
primeiro quadrante.
-0.5
-1
-10
4
-5
0
5
10
Capítulo 2 - O Limite de uma função
Sartori, C. S - 5
Domínio: {x }
Domínio: {x  x
Imagem: {y [-1.1]}
Período: 2
IIc.2) Função cosseno:
Imagem: {y
k + /2 ;k }
(- ,-1)(1, )}
Período:
1
IIc.5) Função Cossecante:
0.5
10
0
5
-0.5
0
-1
-10
-5
0
5
-5
10
Domínio: {x }
Imagem: { y
Período: 2
-10
[-1.1]}
-10
Domínio: {x  x
Imagem: {y
IIc.3) Função tangente:
-5
0
k ; k }
5
10
(- ,-1)(1, )}
Período: 2
30
IIc.3) Função Cotangente:
20
10
20
0
10
-10
-20
0
-30
-6
-4
-2
0
2
4
-10
6
-20
Domínio: {x  x
k + /2 ;k }
-7.5
-5
-2.5
0
2.5
5
7.5
}
Imagem: {y
Período:
Domínio: {x  x
IIc.4) Função secante:
Imagem: {y
k ; k }
}
Período: 2
10
II.d) Relações: Soma e subtração de arcos, arco
duplo, arco metade:
5
0
1) Soma e Subtração:
-5
-10
-10
-5
0
5
10
sen( a b )
sen a .cosb sen b.cosa
cos( a b )
cosa .cosb  sen b.sen a
tg ( a b )
5
tga tgb
1  tga. tgb
Capítulo 2 - O Limite de uma função
Sartori, C. S - 6
2) Arcos Duplos:
II - Introdução à teoria de Limite
sen( 2 a )
2 sena.cosa
cos( 2 a )
cos2 a sen2 a
tag( 2 a )
2 tga
1 tg 2 a
3 ) Transformação Soma-Produto:
1
1
sen( A B ) 2 sen ( A B ) cos ( A
2
2
1
1
sen( A B ) 2 cos ( A B ) sen ( A
2
2
1
1
cos( A B ) 2 cos ( A B ) cos ( A
2
2
1
1
cos( A B ) 2 sen ( A B ) sen ( B
2
2
B)
B)
B)
A)
Vizinhança de um ponto:
Como os números reais são representados por pontos de
uma reta, através de suas abcissas, é costume utilizar a palavra
“ponto” em lugar de número”.
Dizemos que um número real x é ponto interior a um
conjunto dado C se esse conjunto contém um intervalo (a,b), que
por sua vez contém x, isto é :
x  (a,b)  C
Segundo essa definição, todos os elementos de um
intervalo aberto são pontos interiores desse intervalo. O interior
de um conjunto C é o conjunto de todos seus pontos interiores.
Logo, o intervalo (a,b) é seu próprio conjunto interior. Também
é o interior do intervalo fechado [a,b].
Dizemos que o conjunto C é aberto, se todo ponto de C
é interior a C, isto é, se o conjunto coincide com seu interior. O
conjunto vazio é aberto pois coincide com seu interior, que é
vazio.
Denomina-se vizinhança de um número ou ponto a a
qualquer conjunto que contenha a interiormente. Se esse
conjunto estiver simetricamente distribuido, com a no centro, e à
distância de + e - de a; dizemos que temos uma vizinhança
de centro a e de raio . Podemos representar da seguinte
maneira:
V (a-,a+)
Representamos na reta real:
a-
a+
a
x


Podemos considerar uma vizinhança de a excluindo o
próprio valor de a:Denominamos V’(a):
V’(a)= V(a)-{a}={x  0 <
0
x a
}
Diz-se que o número a é ponto de acumulação de um
conjunto C se toda vizinhança de a contém infinitos elementos
de C. Equivale-se dizer que: toda vizinhança de a contém algum
elemento de C diferente de a. Ou: Dado  > 0 :V’(a) contém
algum elemento de C.
Um ponto de acumulação de um conjunto pode ou não
pertencer ao conjunto. Exemplo: os pontos a e b de um intervalo
aberto (a,b) são pontos de acumulação desse conjunto, mas não
pertencem a ele. Todos os pontos do intervalo também são seus
pontos de acumulação e pertencem a ele.
Dizemos que um ponto x é ponto de aderência de um
conjunto C, ou ponto aderente a um conjunto C, se qualquer
vizinhança de x contém algum elemento de C. Isso significa que
x pode ser um elemento de C ou não, se não for será ponto de
acumulação de C. O conjunto dos pontos aderentes a C é
chamado de fecho ou aderência de C, denotado pelo símbolo C
. Observe que C é a união de C com o conjunto C’de seus
pontos de acumulação.
C
6
C C
Capítulo 2 - O Limite de uma função
Sartori, C. S - 7
Diz-se que um conjunto é fechado quando ele
coincide com sua aderência: C C C  C , ou
seja, quando ele contém todos seus pontos de
acumulação: C
C . Esse é o caso de um intervalo
[a,b], do tipo que já se conhecia como “fechado”.
Como exemplo citamos o conjunto:
3. Dê 2 pontos de acumulação das vizinhanças do
problema 2.
II.q - O Limite de uma Função:
Significação intuitiva:
A {12 , 23 , 34 ,..., nn1 ,...}
discreto, pois seus pontos são todos isolados, e
seu único ponto de acumulação é o número 1, que não
pertence ao conjunto. Se o incluirmos ao conjunto A,
teremos a aderência de A, que é o conjunto:
B
A {1} {1, 12 , 23 , 34 ,..., nn1 ,...}
No cálculo e suas aplicações, é importante explorar
valores e comportamento de funções próximos a determinados
números a de seu domínio, ou de valores que não estão
definidos em seu domínio.
Considere a função :
Observamos que esse conjunto C é fechado.
Isso acontece sempre que juntarmos o conjunto C com
o C’ de seus pontos de acumulação, a aderência
C
C  C não terá outros pontos de acumulação
além dos que já estavam em C’. Assim veremos alguns
teoremas que confirmam isso:
Teorema: A aderência
conjunto C é um conjunto fechado.
C
de qualquer
Vamos explorar seu comportamento em torno de a = 2.
Veja que ela não é definida em x = 2 pois torna-se nulo o
denominador. Cuidado! Divisão por zero não é definida!
Com o auxílio do programa Excel construimos a tabela
(x,f(x)) .( Faça: Coluna A1 idêntica à mostrada e digite na
B1:= (A1^3-2*A1^2)/(3*A1-6))
Teorema:
a) A interseção de um número finito de
conjuntos abertos é um conjunto aberto.
a) A união de uma família qualquer de
conjuntos abertos é um conjunto aberto.
1,9000000000
1,9900000000
1,9990000000
1,9999000000
1,9999900000
1,9999990000
1,9999999000
1,9999999900
1,9999999990
1,9999999999
Teorema: Um conjunto F é fechado se e
somente se seu complementar A = FC=R-F é aberto.
Teorema: A união de um conjunto finito de u
conjuntos fechados é um conjunto fechado.
Exercícios:
1.
Dada o centro a e o raio , represente na
f ( x)
 = 0,1 e a =1
f ( x)
 = 0,1 e a =-2
d)  = 0,1 e a =1/2
e)
 = 0,03 e a =1/5
f)
 = 0,025 e a =4
g)  = 0,005 e a =-5
2. Escreva na forma de intervalo aberto as vizinhanças
do problema anterior.
x 2 ( x 2)
3( x 2)
Se x2 podemos simplificar e vemos que:
b)  = 0,2 e a =2
c)
1,2033333333
1,3200333333
1,3320003333
1,3332000033
1,3333200000
1,3333320000
1,3333332011
1,3333333333
1,3333333333
1,3333333333
Parece que quanto mais próximo de 2 está x, mais
próximo de 4/3 está f(x); entretanto não podemos ter certeza
disto pois calculamos apenas alguns valores da função para x
próximos de 2. Para obtermos um valor mais convincente
fatoramos o numerador e o denominador de f(x):
reta as vizinhanças dadas V (a-,a+):
a)
x3 2x 2
3x 6
f ( x)
Veja que o ponto
x2
3
4
(2, ) deve ser omitido para essa
3
função. Assim, quanto mais próximo de 2 estiver x, mais
próximo de 4/3 estará f(x).
Em geral, se uma função f é definida em todo um
intervalo aberto contendo um número real a, exceto
possivelmente no próprio a podemos perguntar:
7
Capítulo 2 - O Limite de uma função
Sartori, C. S - 8
1.
A medida que x está cada vez mais
próximo de a (mas x a) o valor de f(x)
tende para um número real L?
2. Podemos tornar o valor da função f(x) tão
próximo de L quanto queiramos,
escolhendo x suficientemente próximo de
a (mas x a)?
Caso seja possível isso escrevemos:
lim f ( x)
x
a
senx
x
Veja a tabela abaixo: (Construa no Excel).
x
f ( x)
2,0000000000
1,0000000000
0,5000000000
0,4000000000
0,3000000000
0,2000000000
0,1000000000
0,0100000000
0,0010000000
0,0001000000
0,0000100000
0,0000010000
senx
x
0,4546487134
0,8414709848
0,9588510772
0,9735458558
0,9850673555
0,9933466540
0,9983341665
0,9999833334
0,9999998333
0,9999999983
1,0000000000
1,0000000000
Observe que quanto mais x se aproxima de 0,
tanto atravéz de valores positivos como através de
valores negativos, o valor de f ( x) senxse aproxima
x
de 1. Assim dizemos que esse limite, denominado de
limite trigonométrico fundamental, vale:
senx
lim
1
x 0
x
1 x
x
)
2,0000000000
2,5937424601
2,7048138294
2,7169239322
2,7181459268
2,7182682372
2,7182804692
2,7182816940
2,7182817864
2,7182820308
Veja que há uma certa convergência nas casas decimais.
Provaremos mais tarde que esse limite dessa função, quando x
torna-se incrivelmente grande; diz-se x tende a infinito,
aproxima-se do número de Napier e 2.71828, que é um
número irracional.
1) Definição:
Seja f uma funçãoError! Bookmark not defined.
definida em todo número de algum intervaloError!
Bookmark not defined. aberto I, contendo a, exceto
possivelmente no próprio número a. O limite de f(x) quando x
aproxima-seError! Bookmark not defined. Error!
Bookmark not defined.de a é L, que pode ser escrito por:
lim f ( x ) L
x
a
se para qualquer > 0 , mesmo pequeno, existir um >
0 tal que:
f ( x) L
sempre que 0 x a
Isto significa que os valores da função f se aproximamse de um limite Error! Bookmark not defined.L quando x
aproxima-se de um número a se o valor absoluto da diferença
entre f(x) e L puder ser tão pequeno quanto desejarmos,
tomando x suficientemente próximo a a mas não igual a a.
É importante notar que nada é mencionado sobre o
valor da função quando x=a. Isto é, não é necesssário que a
função seja definida em a para que exista o limite.
Exemplo 3: Seja a função definida por :f(x)=4x-1.
dado que
lim f ( x ) 11 encontre um para
0. 01 tal
x
3
que f ( x ) 11
Mais tarde demonstraremos tal relação.
f ( x ) 11
Exemplo 2 – Considere agora a função:
f ( x) (1
f ( x) (1
1
10
100
1000
10000
100000
1000000
10000000
100000000
1000000000
L
Dizemos que o limite de f(x), quando x tende
para a é L, ou que f(x) se aproxima de L quando x se
aproxima de a.
Exemplo 1 - Outro comportamento
interessante ocorre com a função:
f ( x)
x
1 x
x
)
Vamos tomar valores bastante grandes de x.
De novo construa uma tabela no Excel, nos tempos de
hoje isso é facil e barato.
0. 01 sempre que 0 x 3
Solução:
( 4 x 1) 11 4 x 12 4 x 3
4x 3
0. 01 sempre que 0
x 3
0. 0025 sempre que 0
0. 0025
0
x 3
( 4 x 1) 11
x 3
ou
x 3
0. 01 sempre que
0. 0025
Teorema 1: Se m e b são constantes quaisquer:
lim(mx b) ma b
x
8
a
Capítulo 2 - O Limite de uma função
Sartori, C. S - 9
lim f ( x) lim f ( x) lim f ( x)
Teorema 2: Se c é uma constante, então:
x a
limc c; a
x a
x
L;lim g( x)
a
x
M
a
Teorema
lim f ( x)
x
x
x
a
M
lim (4 x 2 )
lim (2 x 2 )
lim h( x )
x 1
x
Portanto: lim h ( x )
3
x 1
20
L; n Z ;lim[ f ( x )]n
a
x
Ln
a
10
Teorema 6:
Se:
-4
L; n Z ; lim[ n f (x) ]
lim f ( x )
x
a
x
n
a
-2
2
lim f ( x)
Se
L; lim g ( x)
a
x
-20
lim ( f ( x) / g ( x))
x
M,M
a
a
0
Exemplo 6 : Calcule os limites unilaterais em torno de 0 par
x
b)
f ( x)
( x 3 27)
3
x 3
lim
Observe, lembrando da definição da função módulo,
que quando x tende a zero pela esquerda:
Seja
( x 3)( x 2 3x 9)
3
( x 3)
lim
x
a
x se x
0
2 se x
0
f ( x)
lim
x 0
função
lim( x 2
x
3
definida
3x 9)
lim
27
x
por:
0
lim
x
determine
x
x
f ( x)
função:
L/ M
Exemplo 4: Encontre os limites:
a)
0
x
x
x 0 x
x
lim
x 0 x
lim
x
x
x
lim 1
1
lim 1
1
x
0
x
lim f ( x )
x
4
-10
L
Teorema7:
x
3;
x 1
Teorema 5:
Se:
lim f ( x )
3
x 1
Se:
L.M
a
L
lim h( x )
x 1
M
a
lim ( f ( x).g ( x))
x
lim( f ( x) g( x))
4:
L; lim g ( x)
a
x a
x 2 se x 1
Encontre os limites unilaterais:
x 2 se x 1
4
2
h( x )
Teorema 3: Se:
lim f ( x)
x a
Exemplo 5 : Seja h definida por:
0
1
0
0
0.5
2) Limites Unilaterais:
Ao considerarmos o valor de
-4
lim f ( x) L
-2
2
x a
-0.5
estamos interessados nos valores de x num intervalo
aberto contendo a , mas não no próprio, isto é, em
valores de x maiores ou menores do que a. Supomos
que x se aproxima de a pela direita e pela esquerda,
respectivamente.e denotamos por: lim f ( x) L ;
Exemplo 7: Determine os limites :
lim x x
x
lim x x
x
x a
lim f ( x) L .
x a
Teorema:
lim f ( x) L se e somente se
x a
existirem
lim f ( x) ; lim f ( x ) e:
x a
0
x a
9
0
lim x 2
lim x( x)
x
0
lim x( x)
x
0
0 -1
2
x
lim x
x
0
0
0
4
Capítulo 2 - O Limite de uma função
Sartori, C. S - 10
x 0 xr
4
1
xr
lim
x
2
-4
1
i) lim
6
0
1
ii) lim
iii)
0 xr
x
se r é par
se r é ímpar
-2
4
Teorema: Se a é um número real qualquer e se
lim f ( x ) 0 e lim g ( x ) c , onde c é uma constante não nula,
-4
então:
-2
2
x a
x
a
-6
(i) Se c > 0 e se f(x) 0, através de valores positivos de
g( x)
x, lim
3) Limites no infinito
x a f ( x)
(ii) Se c > 0 e se f(x) 0, através de valores negativos
Definição: Seja f uma função definida em todo número
g( x)
de um intervalo aberto (a,+ ) , o limite de f(x), quando
de x, lim
x cresce ilimitadamente é L, que pode ser transcrito como:
x a f ( x)
lim f ( x ) L
(iii) Se c <0 e se f(x) 0, através de valores positivos
x
g( x)
de x, lim
x a f ( x)
Da mesma forma, se x tende a um número
(iv) Se c <0 e se f(x) 0, através de valores negativos
negativo que cresce em módulo e possui no limite o
g( x)
valor L, denotamos por:
de x, lim
f ( x)
x
a
lim f ( x ) L
x
O teorema também é valido se "x a" for substituído
Teorema: Se r é um número inteiro e positivo,
;x
por x a ; x a , x
.
então:
1
1
i ) lim
0 ii ) lim
0
Exemplo 9: Encontre:
r
x
x
x
xr
x2 x 2
x2 x 2
a) lim
lim
x 3 x 2 2 x 3 x 3 ( x 3)( x 1)
Exemplo 8 : Encontre o limite abaixo:
O limite do numerador é 14 e no denominador é 0, o
2 x2 x 5
( 2 x 2 x 5) / x 2
lim
lim
que
pode
ser verificado por:
x
x
3x 2 5x
( 3x 2 5x ) / x 2
1 5
1 5
lim ( x 3)( x 1) lim ( x 3) lim ( x 1) 0. 4 0
2
lim 2
2
x
3
x 3
x 3
2
x x2
x
x
x
lim
Verificamos que o denominador está se aproximando
5
5
3
x
3
lim 3
de 0 através de valores positivos. Aplicando o terorema de
x
x
x
limite (i), teremos:
4) Limites Infinitos:
lim
x2
x 3 x2
Definição: Seja f uma função definida em todo
número do intervalo aberto I contendo um número a,
exceto, possivelmente no próprio número a. Quando x
se aproxima de a, f cresce ilimitadamente, o que é
escrito como:
lim f ( x )
x2 x 2
x 3 x 2 2 x 3 x 3 ( x 3)( x 1)
O limite do numerador é 14 e no denominador é 0, o
que pode ser verificado por:
lim ( x 3)( x 1)
x a
x
x 3
lim
lim ( x 3) lim ( x 1)
x 3
0. 4
0
x 3
Verificamos que o denominador está se aproximando
de 0 através de valores negativos. Aplicando o terorema de
limite (ii), teremos:
é equivalente a
a
lim
x2
x 3 x2
lim f ( x)
x a
2x 3
x 2
x2
b) lim
x a
Caso x se aproxime de a e f(x) decresce
ilimitadamente, escrevemos como:
lim f ( x )
Definição: lim f ( x )
x 2
x a
c) lim
x2
x 3 x2
Teorema: Se r é um número inteiro positivo
qualquer, então:
10
x 2
2x 3
x 2
2x 3
pois lim
x
x2
3 x2
x 2
2x 3
Capítulo 2 - O Limite de uma função
Vemos que: f 1 ( x )
Teorema:
Se lim f ( x )
x
Sartori, C. S - 11
c , onde c é
e lim g ( x )
a
x
a
x
lim
lim [ f ( x ) g ( x )]
x
x a
c, onde c é
e lim g ( x )
x a
x a
uma constante qualquer, exceto 0, então:
(i) Se c > 0
x
lim
x
c onde c é
e lim g ( x )
x a
f1 ( x )
uma constante qualquer, exceto 0, então:
(i) Se c > 0
(ii) Se c < 0
a
a
a ;x
2
x
2
2
x 2
2
x 2
lim
2
x
x
2
x 2
x
x 2
2
e
2
6
O teorema também é valido se "x
substituído por x
lim
x
8
lim [ f ( x ). g ( x )]
x
2
x
y
lim [ f ( x ). g ( x )]
x
e
x
, observando suas assíntotas para:
x 2
x
x
2
2
: y = 2 e x = 2 e para f 2 ( x )
:y
x 2
x 2
=-2ex=2
f2 ( x)
x a
x
x 2
A seguir representamos os gráficos de f 1 ( x )
a
Teorema:
Se lim f ( x )
2
x
x 2
horizontais:
x
a
2
2
x 2
2
Assíntotas
x
lim 2
x 2
x
lim [ f ( x ). g ( x )]
e f2 ( x)
x
2
lim [ f ( x ). g ( x )]
(ii) Se c < 0
lim
Assíntotas verticais:
uma constante qualquer, então:
Teorema:
Se lim f ( x )
x
x 2
2
a ,x
;x
4
a" for
.
y=2
y=[(x/(x-2)]1 /2
2
x=2
0
5) Assíntotas:
x
-2
Definição: Diz-se que a reta x=a é uma
assíntota vertical do gráfico de uma função f se pelo
menos uma das afirmações seguintes for verdadeira:
(i)
lim f ( x)
x
(ii)
(ii)
-6
a
lim f ( x)
(iv)
lim f ( x)
x
-10
-8
-6
-4
-2
0
2
4
6
a
(iii)
x
y=-[x/(x-2)]1/ 2
-8
lim f ( x)
x
y=-2
-4
a
6) Continuidade de uma função:
a
Definição: Diz-se que a reta y=b é uma
assíntota horizontal do gráfico de uma função f se
pelo menos uma das afirmações seguintes for
verdadeira:
(i) lim f ( x ) b
(ii) lim f ( x ) b
x
Continuidade em um número:
Definição: Diz-se que uma função é contínua em um
número se, e somente se as seguintes condições são satisfeitas:
(i) Existe f(a)
(ii) Existe lim f ( x )
x
Exemplo 10 : Encontre as assíntotas verticais
e horizontais da equação xy 2
um esboço do gráfico:
Resolvendo a equação: y
2 y2 4 x
x
0 e trace
(iii) lim f ( x )
a
f (a)
x a
2
x
x 2
Se uma ou mais destas condições não for verificada em
a, dizemos que a função é descontínua em a.
Exemplo 6) A função do exemplo 5 é descontínua em
x=2, pois não é definida neste x.
11
Capítulo 2 - O Limite de uma função
Exemplo 11:
f ( x)
x
Sartori, C. S - 12
Seja a função definida por:
3 se x
2 se x
x 3
3
Discuta
3
0
f (3)
sua
Definição: Dizemos que uma função f é contínua no
número a à direita se e somente se as três condições abaixo
forem satisfeitas:
(i) Existe f(a)
(ii) Existe lim f ( x )
que:
Portanto a
2.
x
x 3
Exemplo 12: Discutir a continuidade da
1
função: f ( x )
x 2
Esta função não é contínua em x=2 pois seu
valor não é definido.
Definição: Dizemos que uma função f é contínua no
número a à direita se e somente se as três condições abaixo
forem satisfeitas:
(i) Existe f(a)
(ii) Existe lim f ( x )
x
polinomial é
Teorema 3. Uma função racional é contínua
em todo número do seu domínio.
Teorema 4. Se lim g ( x )
x
b e se a função f
a
é contínua em b,
lim ( fog( x )) f (b)
lim ( f ( g ( x )))
x a
x a
a
(iii) lim f ( x )
Teorema 1. Se f e g são funções contínuas em
um número a, então:
I) f+g é contínua em a
II) f-g é contínua
em a
III) f.g é continua em a
IV) f/g é contínua
em a desde que g(a) 0
f ( lim g ( x ))
x a
Definição: Diz-se que uma função é contínua em
um intervalo aberto se e somente se ela for contínua em
todo número do intervalo aberto.
f (a)
x a
Observação: dizemos que a descontinuidade de uma
função é essencial quando não existir o limite da função no
ponto; é removível quando existir o limite da função.
Trataremos agora a descontinuidade com um puco de
rigor.
Seja a um ponto de acumulação do domínio D de uma
função f; dizemos que f é descontínua em x = a se, ou f não tem
limite unilateral em a, ou esse limite existe e é diferente de f(a)
ou f não está definida em a. Analogamente define-se
descontinuidade à esquerda e descontinuidade à direita. De
acordo com essa definição, estamos admitindo que um ponto
possa ser descontinuidade de uma função mesmo que ele não
pertença ao domínio de f. A rigor, não deveríamos assim admitir,
só deveríamos aceitar descontinuidades em pontos pertencentes
ao domínio de f. Mas é natural considerar o que se passa nas
proximidades de pontos de acumulação do domínio de uma
função, mesmo que tais pontos não pertençam ao domínio.
Como exemplo observe que as funções:
f ( x)
Continuidade em um intervalo
f (a)
x a
II.r - Teoremas sobre continuidade:
função
a
(iii) lim f ( x )
condição (iii) não é satisfeita; a função é descontínua
em x=3.
Teorema 2. Uma
contínua em todo número.
f ( c)
x c
continuidade em x=3.
Observe
lim f ( x) lim x 3
(iii) lim f ( x )
senx
; g ( x)
x
x
x
; h( x)
1
; t ( x)
x
sen
1
x
são todas contínuas em seu domínio: x -{0} e
embora x = 0 não pertença a esse domínio é natural considerar o
que acontece com essas funções quando x tende a zero, tanto
pela esquerda como pela direita. Identifique as curvas nos
gráficos abaixo:
Definição: Dizemos que uma função cujo
domínio inclui o intervalo fechado [a,b] é contínua em
[a,b], se e somente se for contínua para todo c (a,b) e
se ela for contínua em a à direita e em b à esquerda e
também, para
c (a,b) as condições abaixo forem
satisfeitas:
(i) Existe f(c)
(ii) Existe lim f ( x )
x c
12
Capítulo 2 - O Limite de uma função
Sartori, C. S - 13
Teorema (Do valor intermediário)
2
1.5
Seja f uma função contínua num intervalo I=[a,b], com
f(a) f(b). Então, dado qualquer número d compreendido entre
f(a) e f(b), existe c (a,b) tal que f(c) = d. Em outras palavras,
f(x) assume todos os valores compreendidos entre f(a) e f(b),
com x variando entre (a,b).
1
0.5
0
-0.5
-1
Teorema :
-1.5
-10
-5
0
5
De acordo com a nossa definição, a primeira
funçáão f(x) seria classificada como descontínua em x =
0 simplesmente por não estar aí definida. Atribuindo o
valor 1 em x = 0 ela será definida e será contínua em
todo x. Por isso dizemos que sua descontinuidade é
removível. A segunda, g(x), tem limites laterais
diferentes quando x tende a 0. Ela será contínua à
direita se impusermos g(0)=1 e contínua à esquerda se
impusermos g(0)=-1. A terceira função tende a
quando x tende a 0.Não há pois, como remover a
descontinuidade, o que acontece com a função t(x) por
não apresentar limite.
A descontinuidade é de primeira espécie ou do
tipo salto quando a função possui, no ponto
considerado, limites à direita e à esquerda porém
distintos. É o caso da função g(x). A descontinuidade é
de segunda espécie quando, a função tende a
no
ponto considerado (caso da função h(x)), ou não tem
limite neste ponto (caso da função t(x)).
10
Se f é uma função contínua num intervalo I = [a,b] ,
então f(I) é também um intervalo [m,M] , onde m e M são os
valores mínimo e máximo respectivamente, da função f.
Teorema :
A imagem de qualquer intervalo por uma função
contínua f é um intervalo.
Teorema :
Toda função f , contínua e injetiva num intervalo I é
crescente ou decrescente. Sua inversa também é contínua.
Teorema do Confronto ou Sanduíche:
Suponhamos que f(x) h(x) g(x) para todo x em um
intervalo aberto contendo a , exceto possivelmente para o
próprio a . Se:
lim f ( x)
x
L
lim g ( x)
x
a
Então:
Teorema – Os pontos de descontinuidade de
uma função monótona f num intervalo I (limitado ou
não) só podem ser do tipo salto; e formam um conjunto
no máximo enumerável.
Definição:
Chama-se conjunto compacto a todo
conjunto C que seja limitado e fechado.
Um conjunto C diz-se compacto se toda
sequência xn
C possui uma
subsequência convergindo para um ponto
de C.
Teorema: Todo conjunto compacto C possui
máximo e mínimo.
Teorema : Se f é uma função contínua num
domínio compacto D, então f(D) é um conjunto
compacto.
Teorema (de Weierstrass):
a
lim h( x)
x
a
L
Como aplicação desse teorema vamos demonstrar que
senx
lim
1 , que é o limite trigonométrico fundamental.
x 0
x
É possível mostrar que, para x pequeno ocorre uma
ordem entre algumas funções de acordo com:
Senx<x <Tgx
Isso é ilustrado no gráfico a seguir:
Seja f uma função com domínio compacto D.
Então f assume valores máximo e mínimo em D, isto é,
existem pontos a e b em D tais que:
f(a) f(x) f(b)
Para todo x D.
13
Capítulo 2 - O Limite de uma função
Sartori, C. S - 14
Exercícios:
1
1) Encontrar os limites indicados:
0.75
a)
0.5
lim
x
0.25
-0.5
e) lim
x
-0.75
-3
-2
-1
0
1
2
3
x
x
senx
x
tgx
senx senx senx
Simplificando, invertendo e trocando
ordenação, consequentemente obteremos:
a
senx
1
x
cos x
x
a)
0
2
7x 3
4 t
t
0
j) lim
9
2 x 3 5x 2 2 x 3
x 3 4 x 3 13x 2
4x 3
x 9 3
encontre seu limite quando
x
f ( x)
b)
teremos:
3 se x
2
3
x se x
2
Encontre:
2
lim f ( x )
x
senx
lim
1
x 0
x
x
lim f ( x )
x
e portanto, aplicando o teorema do confronto,
2
x 2 se x 1
4) Dada f ( x)
1 x se x 1
Encontre: a) lim f ( x ) b) lim f ( x )
Aplicações:
x
x 1
A velocidade média é definida como sendo a
razão entre a variação da posição num certo intervalo de
tempo:
s
t
v
Para definirmos velocidade instantânea
necessitamos que o intervalo de tempo tenda a zero, ou
seja a velocidade instantânea é o limite quando o
intervalo de tempo vai a zero da razão entre a variação
da posição e o intervalo de tempo:
lim
t
0
1
5) Dada f ( x ) 3 2 x 4 encontre:
a) lim f ( x ) b) lim f ( x ) c) lim f ( x )
x
v
3 2 x2
h) lim
t
F ( x)
3) Dada
lim 1 1
0
2
x2
x tende a 0.
Observamos que:
lim cos x
x
x
0
2) Se
f) lim
3x 1 1
i) lim
1 x2 2 x
x3 1
x 1 x 1
x 2
x
0
x
d) lim
2 x 2
g) lim
x2 2 x
b) lim
x 12
x 1 x2 1
x3 8
-0.25
x
3 x2
x 1
c) lim
0
x 2 5x 6
2
x
6) Dada f ( x )
x
x
2
x 2
encontre:
a) lim f ( x ) b) lim f ( x ) c) lim f ( x )
x
0
x
0
x 0
7) Discutir a continuidade das funções dos problemas
4), 5) e 6).
s
t
8) Determine os limites:
a) lim
x
c) lim
x
e) lim
x
14
2x 1
5x 2
b) lim
x
4 x2 3
2 x2 1
x2 4
4 x3 2 x2 5
d) lim
x 4
x
8x3 x 2
x2 1 x
Capítulo 2 - O Limite de uma função
x
f) lim
4x
x
2 t2
t
x
t
4
0
2 t2
0
3 x2
x2 9
m) lim
x
x 3
x 0
x 3
3
1 1
2y 4
n) lim
o) lim (
)
5y 3
x 0 x x2
y
1
3
p) lim (
)
2
x 2 x 2 x
4
5 x
q) lim
x
33 x
l) lim
4
x2
2
e) f ( x )
g) f ( x )
x2
d) f ( x )
5x 6
x2
2
b)
3 xy 2 x 4 y 3
x2 y2 x2 4 y2
c)
( y2
1)( x 3)
2
x 5
4 x2
x2 9
9
0
0
6
;(3, 7);[ 6, 4];(
, 0)
b)
x2
f ( x)
9 ;(
, 3),(
, 3],( 3, 3),[ 3,
)
c)
2 x 3 se x
f ( x)
2
x 5 se 2 x 1 ; (
f ( x)
f ( x)
a) f ( x )
11) Determine se a função é contínua ou
descontínua nos intervalos indicados:
a) f ( x )
b)
3x
7 se x
4
kx 1 se x
4
kx 1 se x
2
2
kx se x
2
cx k se 1
,1); ( 2,
x
4
4
x2 4
2)2
10) Nos exercícios abaixo, encontrar as
assíntotas verticais e horizontais e faça um esboço do
gráfico:
a)
f ( x)
3
x2 3
x
h) f ( x )
)
13) Trace um esboço do gráfico e discuta a
continuidade das funções abaixo:
3x
f) f ( x )
x2 4
4 x2
, 2 );[ 2 ,
2 x se x
(x
1
c) f ( x )
a)
c)
b) f ( x )
5 x
x
( 2 , 2 ),[ 2 , 2 ]; (
x
x se x 1
9) Nos problemas abaixo, encontre as
assíntotas verticais e horizontais e trace um esboço do
gráfico.
a) f ( x )
2
2
12) Nos exercícios abaixo determine o valor das
constantes de k e c que fazem com que a função f seja
contínua em (- ,+ ) e trace um esboço da função resultante:
4
3 x2
x
k) lim
x
d) f ( x )
4
t 2
i) lim
3 x2
x
j) lim
2 t2
t
t 2
h) lim
t 2
g) lim
4
Sartori, C. S - 15
); ( 2,1);[ 2,1)
3 x se x 1
15
x 2
b) h ( x )
( x 3)( 4
x)
Capítulo 2 - O Limite de uma função
Sartori, C. S - 16
II - RESUMOS
Triângulos
Y = Secx
C
1.
Áreas
b
A= r2
A
A = bh/2
r
a
B
D
c
h
senA senB senC
a
b
c
2
2
2
c
a b 2ab cos C
b
A = b.h
D=A+C
A = r2 /2
r
(s=r )
s
1 x
r
n
2
A r2 (
sen )
Funções trigonométricas e Identidades
trigonométricas
1 x
ex
sen =y/r
tg =y/x
csc =r/y
cos =x/r
cotg =x/y
sec = r/x
y
ln(1 x)
x
sen(
2
cos(
2
tg
cos 2
sec2
c sec2
sen2
cos 2
cos 2
sen(
cos(
)
)
tg (
sen
cos
cos
sen 2
sen
cos
cos
n
Teorema Binomial
nx n(n 1) x 2
1
...( x 2 1)
1!
2!
nx n(n 1) x 2
1
...( x 2 1)
1!
2!
Expansões em séries
x2 x3
xn
1 x
...
2! 3!
n 0 n!
)
sen
cos
cos
)
sen
2 cos 2
1 2sen 2
1
sen cos
cos sen
cos cos  sen sen
tg
tg
)
1  tg tg
) cos12 (  )
) cos12 (
)
1
)sen2 (
)
1
x3
3
...( x
3
5
3!
5!
2
4
1)
...
...
4!
ei
cos
isen
i
e
e i
cos
2
i
e
e i
sen
2i
Funções Hiperbólicas
ex e x
senhx
2
x
e e x
cosh x
2
2
cosh x senh 2 x 1
sen
cos
sen 2
1
2
1 tg
1 cot g 2
2sen cos
2sen12 (
2cos12 (
2sen12 (
x2
2
x
tghx
cot ghx
16
1
; sec hx
tghx
2!
senhx
coshx
1
; cos sec hx
cosh x
1
senhx
Capítulo 2 - O Limite de uma função
Sartori, C. S - 17
Números Binomiais:
n!
; 0! 1 n! n( n 1)...1
( n p)! p!
n
Volumes
p
Alfabeto Grego:
Cilindro: V= r2h
Paralelepípedo: V=abc
alfa (
, beta
gama (
delta (
épsilon (
zeta (
eta (
teta (
iota (
capa (
lambda (
mu (
nu (
csi (
ômicron (
pi (
ro (
sigma (
tau (
upsilon (
fi (
chi (
psi (
omega (
Prisma: V = Sb.h
Pirâmide:
V = Sb.h/3
Cone:
V= r2h/3
Propriedades: Funções Logarítmicas e Exponenciais:
i) log a x
iii) log a x1
Vetores
iv) log a (
ˆj kˆ kˆ 1
kˆ kˆ iˆ 0
ˆj kˆ kˆ 0
kˆ iˆ; kˆ iˆ ˆj
iˆ iˆ ˆj
iˆ ˆj ˆj
iˆ iˆ ˆj
iˆ ˆj kˆ; ˆj
x
a y ii) log a 1 0
log a x 2
log a ( x1 .x 2 )
y
x1
)
x2
v) log a x n
log a x1 log a x 2
n log a x
vi) Se a 1 e log a x 2
vii) Seja a
0, b
que formam uma base ortonormal do R3
viii) a lo ga x
x
ax iˆ a y ˆj az kˆ
 
a b
 
b a
iˆ
ˆj
kˆ
ax
ay
az
bx
by
bz
log a x1
vii) Se 0 < a 1 e log a x 2
Qualquer vetor pode ser escrito como CL de {iˆ, ˆj, kˆ} ,

a
i) a x . a y
ii )
ax
ay
v ) a0
a
ax
x1
log a x1
0 e a, b 1
y
x2
x2
x1
log a x
log a b
log b x
iii ) ( a x ) y
a x. y
y
ax
y
iv )
1
ay
x
vi ) a
ax
1
ax
x
Produtos especiais e fatoração:
1) ( x
2) ( x
3) x
4) x
2
3
5) ( x
y )2
3
x 2 2 xy
3
2
y)
x
2
(x
y )( x
(x
y )( x  xy
y
y
3
y )n
xn
3x y 3xy
1
2
y
3
viii ) Se a
y)
2
n
vii ) Se a x
y2
xn 1y
y2 )
n
2
x n 2 y 2 ...
n
n
yn
17
a ye a
x
y
1
a e 0<a
x
1
y
x
y
Capítulo 2 - O Limite de uma função
Sartori, C. S - 18
Referências:
“Matemática”, Astor e Remo, Volume 1,
Volume 2 e Volume 3. Editora Scipione.
"O Cálculo com Geometria Analítica",
Swokovski, Volume 1.
"O Cálculo com Geometria Analítica", L.
Leithold, Volume I.
"Introdução à Análise Matemática", Geraldo
Ávila. Editora Edgard Blücher
"Mathematica", Stephen Wolfram, A System
for doing Mathematics by computer. Addison Wesley
Publishing Company
18