k - Facom

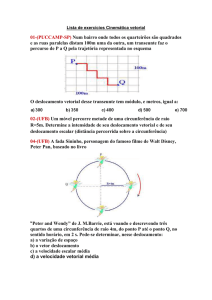
Modelos Algébricos Alternativos
Modelos: Vetorial Generalizado, LSI e Redes Neurais
MODELO VETORIAL GENERALIZADO:
Independência de termos = ortogonalidade entre vetores
de termos no vetorial clássico => ki . kj = 0
Espaço vetorial generalizado : vetores de termos não
são necessariamente
ortogonais, o espaço vetorial é
definido com base nos documentos.
Definições:
k ={k1, k2,..., kt} conjunto de termos
wi,j ∈ {0,1} peso associado a cada par (ki , dj )
conjunto de 2t mintermos mi representando todas as
possibilidades de
combinação de termos em
documentos, i.e.,
m1 = (0, 0, ..., 0)
base Rt
m2 = (1, 0, ..., 0)
m3 = (0, 1, ..., 0)
m4 = (1, 1, ..., 0)
...
m2t = (1, 1, ..., 1)
associe um vetor mi =a cada mintermo mi em
uma base R2t
Exemplos de vetor:
m1 = (1, 0, ..., 0)
m2 = (0, 1, ..., 0)
m2t = (0, 1, ..., 0)
Espaço vetorial generalizado: é definido pelo mintermos
associados a pelo menos um documento da coleção
Obs: embora existam 2t possibilidades de mintermos no
máximo N podem estar ativos
Vetor ki associado ao termo ki :
ki
= Σ∀r, k
i ∈ mr
ci,r . mr
/
sqrt (Σ∀r, k
i ∈ mr
ci,r2 )
onde
ci,r = Σ∀
j | dj = mr
wi,j
Representação de documentos e consultas:
dj = Σ∀i wi,j . ki
Ranking:
coseno
q = Σ∀i wi,q . ki
sim(dj , q) = dj . q / |dj| . |q|