Aula 3 – 2 de junho

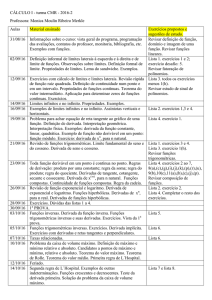
Cronograma FUV
Aula1 -26 de Maio
Limites




Intuição e interpretação gráfica
Definição por e .
Limite da função constante e linear.
Exemplo da não existência do limite num ponto
Aula 2 -29 de Maio
Propriedades dos Limites.




Limites da Soma
Limite do Produto
Limite do Quociente
Limites de Potências, Raízes.
Limites Básicos



Polinômios
Módulos
Funções Racionais
Aula 3 – 2 de junho
Continuidade.



Definições, interpretação gráfica.
Continuidade da função constante e linear.
Exemplos de funções descontínuas
Propriedades da Continuidade





Continuidade da soma de funções.
Continuidade do Produto de Funções
Continuidade do Quociente.
Continuidade da Composta.
Continuidade de funções inversas;
Continuidade das funções Polinomiais e Racionais.
Aula 4 - 5 de junho
Teorema do Valor Intermediário.
Teorema do Confronto.



Limite fundamental.
Continuidade das funções trigonométricas
Continuidade da exponencial.
Exemplos de cálculo de limites.
Aula 5 -9 de junho
Limites Infinitos e no Infinito. Assíntotas.
Aula 6-16 de junho
Derivada.




Motivação: Taxa de variação e tangente.
Interpretação gráfica.
Definição como quociente de Newton.
Derivadas elementares: funções constantes, lineares e quadráticas, etc.
Aula 7 -19 de junho
Regras de derivação.



Derivada da soma
Derivada do Produto
Derivada do quociente
Regra da cadeia.
Aula 8- 23 de junho



Derivada de funções inversas.
Derivação de funções logarítmicas e funções exponenciais.
Derivadas de funções trigonométricas e de funções trigonométricas inversas.
Aula 9- 26 de junho
Derivadas de ordem superiores e derivadas de funções implícitas. Taxas Relacionadas.
Aula 10--30 de junho Prova I
Aula 11-3 de julho
Teorema do Valor médio.
Máximos e mínimos, absolutos e relativos I.


Definições,
Interpretações gráficas e propriedades.
Aula 12-7 de julho
Máximos e mínimos, absolutos e relativos II.

Testes da 1a e 2a derivada, para máximos e mínimos relativos.
Recesso
Aula13 – 21 de julho
Aplicações: Construções de gráficos.
Aula 14 – 24 de julho
Formas indeterminadas e a regra de L’Hôpital
Aula15- 28 de julho
 Polinômio de Taylor.
 Integral indefinida
Aula 16 – 31 de julho
Integral definida




Somas de Riemann Inferiores e superiores.
Definição de Integral definida.
Exemplos simples
Propriedades da integral definida
Aula 17 – 4 de agosto



Propriedades da integral definida
Teorema fundamental do cálculo.
Cálculo de áreas entre duas curvas.
Aula 18 – 7 de agosto
Métodos de integração I.
 Integração por mudança de variável
 Integração por partes.
Aula 19 – 11 de agosto
Métodos de integração II.

Integração de funções racionais por frações parciais.
Aula 20 – 14 de agosto
Métodos de integração III.

Integração de potências de funções trigonométricas.
Aula 21- 18 de agosto
Volumes e Áreas de um sólido de revolução
Aula 22 – 21 de Agosto
Aplicações: (algumas destas)



Volumes por Cascas Cílindricas
Trabalho
Comprimento de arco.
Aula 23 -25 de Agosto - Prova 2
Aula 24 -28 de Agosto - Prova Substitutiva