FUNÇÃO EXPONENCIAL

FUNÇÃO EXPONENCIAL
DEFINIÇÃO: Chama-se função exponencial qualquer função f: R→R dada por uma lei da forma f(x) =ax, em que a é
um número real dado, a>0 e a≠1.
Exemplos: y = 2x ; f(x)=(1/3)x; f(x) = (1 + x)1/x
Note que uma função exponencial tem uma base constante e um expoente variável.
GRÁFICO DE UMA FUNÇÃO EXPONENCIAL
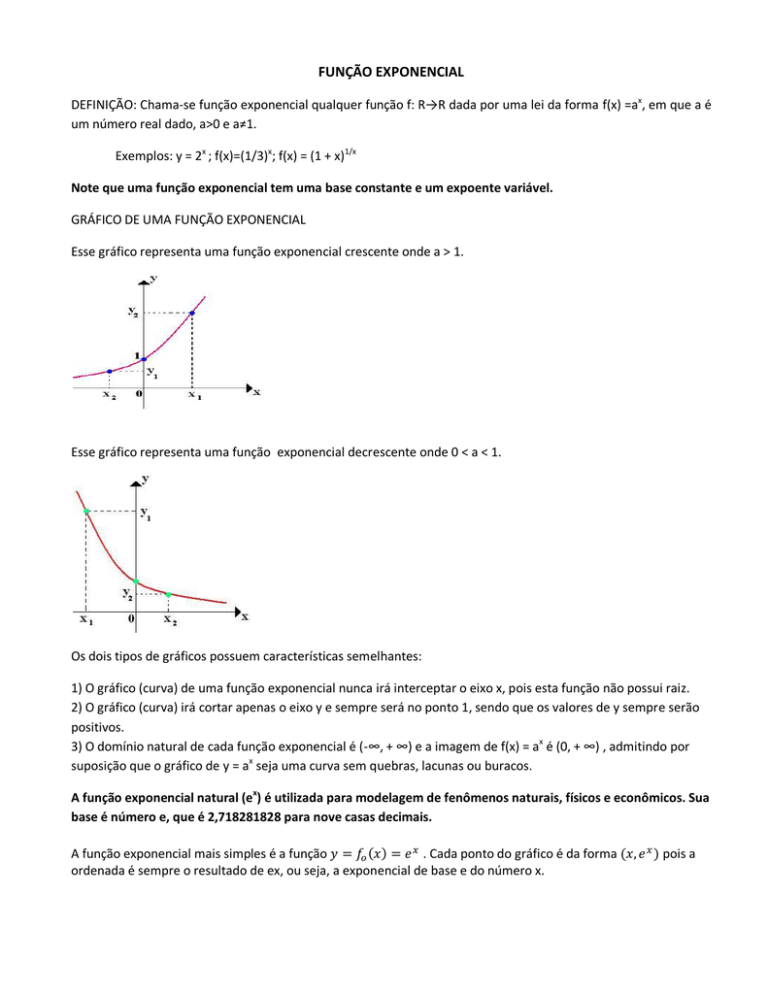
Esse gráfico representa uma função exponencial crescente onde a > 1.
Esse gráfico representa uma função exponencial decrescente onde 0 < a < 1.
Os dois tipos de gráficos possuem características semelhantes:
1) O gráfico (curva) de uma função exponencial nunca irá interceptar o eixo x, pois esta função não possui raiz.
2) O gráfico (curva) irá cortar apenas o eixo y e sempre será no ponto 1, sendo que os valores de y sempre serão
positivos.
3) O domínio natural de cada função exponencial é (-∞, + ∞) e a imagem de f(x) = ax é (0, + ∞) , admitindo por
suposição que o gráfico de y = ax seja uma curva sem quebras, lacunas ou buracos.
A função exponencial natural (ex) é utilizada para modelagem de fenômenos naturais, físicos e econômicos. Sua
base é número e, que é 2,718281828 para nove casas decimais.
A função exponencial mais simples é a função
. Cada ponto do gráfico é da forma
ordenada é sempre o resultado de ex, ou seja, a exponencial de base e do número x.
pois a
O domínio da função
é
e a imagem é o conjunto
.
PROBLEMAS:
1) Duas populações, designadas por F e G, têm os respectivos crescimentos expressos por f(t) = 36 + t2 e g(t) =
10(2t), sendo t o número não negativo que representa o tempo em meses. Então analise as seguintes afirmações:
a) A população G duplica a cada mês.
b) g(51) – g(50) = g(50)
c) Quando t=1 a população F é menor do que a população G.
d) Em nenhum tempo a população F será igual à população G.
2) (Uneb-BA) A expressão P(t) = k . 20,05t fornece o número P de milhares de habitantes de uma cidade, em função
do tempo t, em anos. Se em 1990 essa cidade tinha 300 000 habitantes, quantos habitantes, aproximadamente,
ela possuia no ano 2 000?
a) 352 200
b) 401 000
c) 423 000
d) 439 000
e) 441 000
3) (UFPA) Uma reserva florestal possui 10 000 árvores. Determine em quantos anos a quantidade de árvores
estará reduzida à oitava parte, se a função que representa a quantidade de árvores por ano é y(t) = 10 000 . 2-t.
4) Esboce o gráfico de
e de
5) Esboce o gráfico da função
, comparando-os com o gráfico de
.
.
6) Resolva as equações exponenciais:
a)
b)
7) Determine o conjunto solução da desigualdade
LOGARITMOS e FUNÇÃO LOGARÍTMICA
Do grego: logos (razão) + arithmos (número)
Definição
Sejam a e b dois números reais. O logaritmo de a na base b é o expoente a que b deve ser elevado
para que o resultado seja a. Em símbolos:
Dizemos que b é a base e a é o logaritmando.
É importante, contudo, definir algumas restrições à base e ao logaritmando:
i)
A base deve ser positiva. Determinar, por exemplo, o logaritmo de 2 na base -10 é
impossível no universo dos números reais, já que apenas as potências de expoentes
inteiros estão definidas para bases negativas.
ii)
A base deve ser diferente de um. Como 1 elevado a qualquer número dá 1, o único
logaritmando possível (com base 1) seria 1.
iii)
O logaritmando deve ser positivo. Nenhum número real positivo tem potências
negativas.
CONSEQUENCIAS
- O logaritmo de 1 em qualquer base a é igual a 0.
log a 1 = 0, pois a0 = 1
- O logaritmo da base, qualquer que seja ela é igual a 1.
log a a = 1, pois a1 = a
- A potência de base a e expoente log a b é igual a b.
a log a b = b
Pois o logaritmo de b na base a é justamente o expoente que se deve dar à base a para que a
potência fique igual a b.
- Se dois logaritmos em uma mesma base são iguais, então os logaritmandos também são iguais.
log a b = log a c ⇒b = c
EXEMPLOS
log 2 4
log 3 81
log 2 1/8
log 7 7
log 5 1
log 1/5 125
8 log 8 5
log 5 (2x+1) = log 5 (x+3)
log 16 0,25
log 2 5 = 2,32
log 5 = 0,699
O logaritmo mais importante nas aplicações é o de base e, que é chamado logaritmo natural, já que
a função
é a inversa da função exponencial natural ex. É comum denotar o logaritmo natural
de x por ln x. Assim:
ln 1 = 0
ln e = 1
ln 1/e = -1
ln (e²) = 2
ln(ex) = x ou e ln x = x
PROPRIEDADES DOS LOGARITMOS
 LOGARITMO DO PRODUTO: Em qualquer base, o logaritmo do produto de dois números
reais e positivos é igual à soma dos logaritmos dos números.
log a (b. c) = log a b + log a c
 LOGARITMO DO QUOCIENTE: Em qualquer base, o logaritmo do quociente de dois
números reais e positivos é igual à diferença entre o logaritmo do dividendo e o
logaritmo do divisor.
log a b/c = log a b - log a c
 LOGARITMO DA POTÊNCIA: Em qualquer base, o logaritmo de uma potência de base real
e positiva é igual ao produto dos expoentes pelo logaritmo da base da potência.
log a br = r. log a b
PROPRIEDADES DOS LOGARITMOS
1) log 2 (3. 4) = log 2 3 + log 2 4
2) log 210
3) log 2 ¾
4) log 6/5
5) log 2 37
6) log 3 1/16
MUDANÇA DE BASE: Converter um logaritmo de certa base para outra base.
log a b = log c b/ log c a
FUNÇÃO LOGARÍTMICA
Dado um número real a (com 0<a ≠ 1), chama-se função logarítmica de base a a função de dada pela
lei:
f(x) = log a x.
Exemplos: y = log 2 x, y = log 10 x e y = log e x.
Principais Características
Função logarítmica
g: lR+
0<a<1
lR
x
Função logarítmica
a>1
g: lR+
lR
x
loga x
loga x
● Domínio = lR+
● Domínio = lR+
● Contradomínio = lR
● Contradomínio = lR
● g(x) = 0 <=> x = 1
● g(x) = 0 <=> x = 1
● A função é estritamente decrescente.
● A função é estritamente crescente.
● x = 0 é assíntota vertical
● x = 0 é assíntota vertical
A função logaritmo natural mais simples é a função y=f0(x)=lnx. Cada ponto do gráfico é da forma
(x, lnx) pois a ordenada é sempre igual ao logaritmo natural da abscissa.
O domínio da função ln é
e a imagem é o conjunto
O eixo vertical é uma assíntota ao gráfico da função.
.
FUNÇÃO LOGARÍTMICA - aplicação
LEI DO RESFRIAMENTO DE NEWTON
A temperatura T de um corpo colocado num ambiente cuja temperatura é T 0 obedece à seguinte
relação:
T = T0 + ke-ct
Nesta relação, T é a medida na escala Celsius, t é o tempo medido em horas, a partir do instante em
que o corpo foi colocado no ambiente, e k e c são constantes a serem determinadas.
PROBLEMAS
1) Considere uma xícara contendo café, inicialmente a 100º C, colocada numa sala de temperatura
20º C. Vinte minutos depois, a temperatura do café passa a ser de 40ºC.
Calcule a temperatura do café 50 minutos depois após a xícara ter sido colocada na sala.
Considerando ln 2 = 0,7 e ln 3 = 1,1, estabeleça o tempo aproximado em que, depois de a xícara ter
sido colocada na sala, a temperatura do café se reduziu à metade.
2) Um laboratório iniciou a produção de certo tipo de vacina com um lote de x doses. Se o planejado é o que o
número de doses produzidas dobre a cada ano, após quanto tempo esse número passará a ser igual a 10 vezes o
inicial? (Use log 2= 0,30)
a) 1 ano e 8 meses
b) 2 anos 3 meses
c) 2 anos e 6 meses
d) 3 anos e 2 meses
e) 3 anos e 4 meses
3) A expressão N(t) = 1500 . 20,2t permite o cálculo do número de bactérias existentes em uma
cultura, ao completar t horas do início de sua observação (t=0). Após quantas horas da primeira
observação haverá 250 000 bactérias nessa cultura?
Dados: log 2 = 0,30; log 3 = 0,48.
4) Na escala Richter, a violência de um terremoto de intensidade I é dada por
.
(a) Determine a intensidade do terremoto de 1908 em San Francisco, que atingiu 8,3 na escala
Ritchter.
(b) Quantas vezes mais intenso foi o terremoto de 1908 em San Francisco que o terremoto de 1995
em Kobe, no Japão, que atingiu 7,1 na escala Richter.
5) Encontre x tal que:
a)
b) ln(x+1)=5
6) Resolva
c) 5x = 7
para x.
7) Use as propriedades dos logaritmos para reescrever a expressão em termos de r, s e t onde
a)
b)
c)
d)
8) Resolva para x:
a)
e) ln 4x – 3 ln (x²) = ln 2
b)
f) 3x = 2
c) ln ( x²) = 4
g) 5-2x = 3
d)
h)
=7
9) Esboce o gráfico de y=2. ln x e o gráfico de
10) No sistema cartesiano abaixo, estão representadas as funções
diferente de zero. Determine o valor de a.
y = 3, onde a é número real