gabarito - Walter Tadeu

COLÉGIO PEDRO II - UNIDADE SÃO CRISTÓVÃO III
1ª SÉRIE – MATEMÁTICA II – PROFº WALTER TADEU
www.professorwaltertadeu.mat.br
1ª Lista de Trigonometria no Triângulo Retângulo
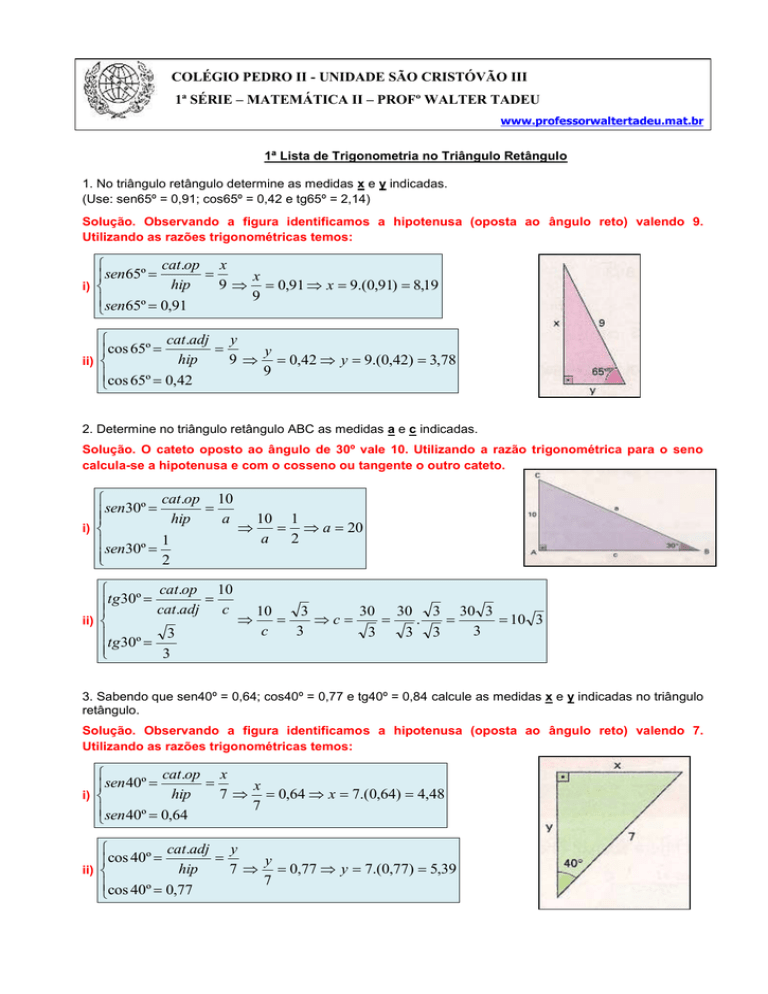
1. No triângulo retângulo determine as medidas x e y indicadas.
(Use: sen65º = 0,91; cos65º = 0,42 e tg65º = 2,14)
Solução. Observando a figura identificamos a hipotenusa (oposta ao ângulo reto) valendo 9.
Utilizando as razões trigonométricas temos:
cat.op x


x
sen65º 
hip
9   0,91  x  9.(0,91)  8,19
i) 
9
sen65º  0,91

cat.adj y


y
cos 65º 
hip
9   0,42  y  9.(0,42)  3,78
ii) 
9
cos 65º  0,42

2. Determine no triângulo retângulo ABC as medidas a e c indicadas.
Solução. O cateto oposto ao ângulo de 30º vale 10. Utilizando a razão trigonométrica para o seno
calcula-se a hipotenusa e com o cosseno ou tangente o outro cateto.

sen30º 


i) 
sen30º 



tg30º 

ii) 
tg30º 

cat.op 10

10 1
hip
a

  a  20
a 2
1
2
cat.op 10

cat.adj c
3
3

10
3
30 30 3 30 3

c

.

 10 3
c
3
3
3
3 3
3. Sabendo que sen40º = 0,64; cos40º = 0,77 e tg40º = 0,84 calcule as medidas x e y indicadas no triângulo
retângulo.
Solução. Observando a figura identificamos a hipotenusa (oposta ao ângulo reto) valendo 7.
Utilizando as razões trigonométricas temos:
cat.op x


x
sen 40º 
hip
7   0,64  x  7.(0,64)  4,48
i) 
7
sen 40º  0,64

cat.adj y


y
cos 40º 
hip
7   0,77  y  7.(0,77)  5,39
ii) 
7
cos 40º  0,77

4. Considerando o triângulo retângulo ABC, determine as medidas a e b indicadas.
Solução. O cateto oposto ao ângulo de 60º vale 12 3 . Utilizando a razão trigonométrica para o seno
calcula-se a hipotenusa e com o cosseno ou tangente o outro cateto.

sen60º 

i) 

sen60º 
cat.op 12 3

hip
a

3
2
12 3
3
24 3

a
 24
a
2
3
cat.adj b

cos 60º 


b 1
24
hip
24


 b
 12
ii) 
24
2
2
1
cos 60º 

2

5. Em um triângulo retângulo isósceles, cada cateto mede 30cm. Determine a medida da hipotenusa desse
triângulo.
Solução 1. Utilizando a razão trigonométrica para seno ou cosseno, temos:
cat.op 30

sen 45º  hip  hip
30
2
60 2 60 2



 hip 
.

 30 2cm
i) 
hip
2
2
2 2
sen 45º  2

2
Solução 2. Aplicando a relação de Pitágoras, temos:
i)
hip 2  cat12  cat 22  hip 2  302  302  hip 2  900  900
 hip  1800  2.3 2.10 2  30 2cm
6. A diagonal de um quadrado mede
perímetro desse quadrado?
6 2 cm, conforme nos mostra a figura. Nessas condições, qual é o
Solução 1. Utilizando a relação trigonométrica do seno, temos:
cat.op cat.op

sen 45º  hip  6 2
cat.op
2
6 2. 2 12



 cat.op 

 6cm

2
2
2
6
2
2
sen 45º 

2

Perímetro  4.6  24cm
Solução 2. Utilizando a fórmula que calcula a diagonal do quadrado em função do lado, temos:
d l 2 6 2 l 2 l 
6 2
2
 6cm Logo o perímetro será (4 x 6) = 24cm.
7. Uma pipa é presa a um fio esticado que forma um ângulo de 45º com o solo. O comprimento do fio é
80m. Determine a altura da pipa em relação ao solo. Dado
2 = 1,41
Solução. Utilizando a relação trigonométrica do seno, temos:
cat.op
x

sen 45º  hip  80
2

 x  80.
 40 2  40(1,41)  56,4m

2
sen 45º  2

2
8. Qual é o comprimento da sombra de uma árvore de 5 m de altura quando o sol está 30º acima do
horizonte? Dado
3 = 1,73
Solução. O comprimento “s” da sombra é o cateto adjacente ao ângulo de 30º. Como é informada a
altura da árvore que representa o cateto oposto o uso da razão
trigonométrica associada à tangente é imediato.

tg30º 


tg30º 

cat.op 5

cat.adj s

3
3
5
3
15 15 3

s

.
 5 3m
s
3
3
3 3
9. Determine a altura do prédio da figura seguinte:
Solução. A altura do prédio é o cateto oposto ao ângulo de 30º. Como é informada a distância do
vértice do ângulo ao prédio, a razão trigonométrica
associada à tangente é imediata.

tg 30º 


tg 30º 

cat.op
h

cat.adj 60

3
3
h
3
60 3

h
 20 3m
60
3
3
10. Para determinar a altura de um edifício, um observador coloca-se a 30m de distância e assim o observa
segundo um ângulo de 30º, conforme mostra a figura. Calcule a altura do edifício medida a partir do solo
horizontal. Dado 3 = 1,73
Solução. Primeiramente calculamos o comprimento “h” do
triângulo formado com o ângulo de visão do observador. A
razão trigonométrica associada à tangente é imediata.
tg30º 
cat.op
h
3

 h  30.tg30º   h  30.

cat.adj 30
3
h  10 3m  10(1,73)  17,3m
A altura do edifício será a soma da altura do triângulo com a do observados: 17,3 + 3 = 20,3m.
11. Observe a figura e determine:
a) Qual é o comprimento da rampa?
Solução. O comprimento da rampa “x” é a hipotenusa do
triângulo retângulo. Como é informado o cateto oposto ao
ângulo de 30º, a razão trigonométrica associada ao seno é
imediata.
sen30º 
cat.op 1,5
1,5
1,5

x

 3m
hip
x
sen30º 0,5
b) Qual é a distância do inicio da rampa ao barranco?
Solução. A distância do início da rampa ao barranco “y” é o cateto adjacente ao ângulo de 30º, a
razão trigonométrica associada à tangente é imediata.

tg30º 


tg30º 

cat.op 1,5

cat.adj
y
3
3

1,5
3
4,5
4,5

y
y
 2,6m
y
3
1,73
3
12. A uma distância de 40m, uma torre é vista sob um ângulo
h da torre se  = 30º.
 , como mostra a figura. Determine a altura
Solução. A altura da torre é o cateto oposto ao ângulo de 30º. Como é informada a distância do
vértice do ângulo à torre da razão trigonométrica
associada à tangente é imediata.

tg30º 


tg30º 

cat.op
h

cat.adj 40
3
3

h
3
40 3

h
 23m
40
3
3
13. Em um triângulo ABC, retângulo em A, o ângulo B mede 30º e a hipotenusa mede 5cm. Determine as
medidas dos catetos
AC e AB desse triângulo.
Solução. O problema descrito pode ser representado pelo desenho mostrado.
Observando a figura identificamos a hipotenusa (oposta ao ângulo reto) valendo 5. Utilizando as
razões trigonométricas temos:
cat.op x


x
sen30º 
hip
5   0,5  x  5.(0,5)  2,5
i) 
5
sen30º  0,5

cat.adj y

cos 30º  hip  5
y
3
5 3

 
y
 (2,5)  (1,73)  4,33
ii) 
5
2
2
cos 30º  3

2