Solução

www.fisicaexe.com.br
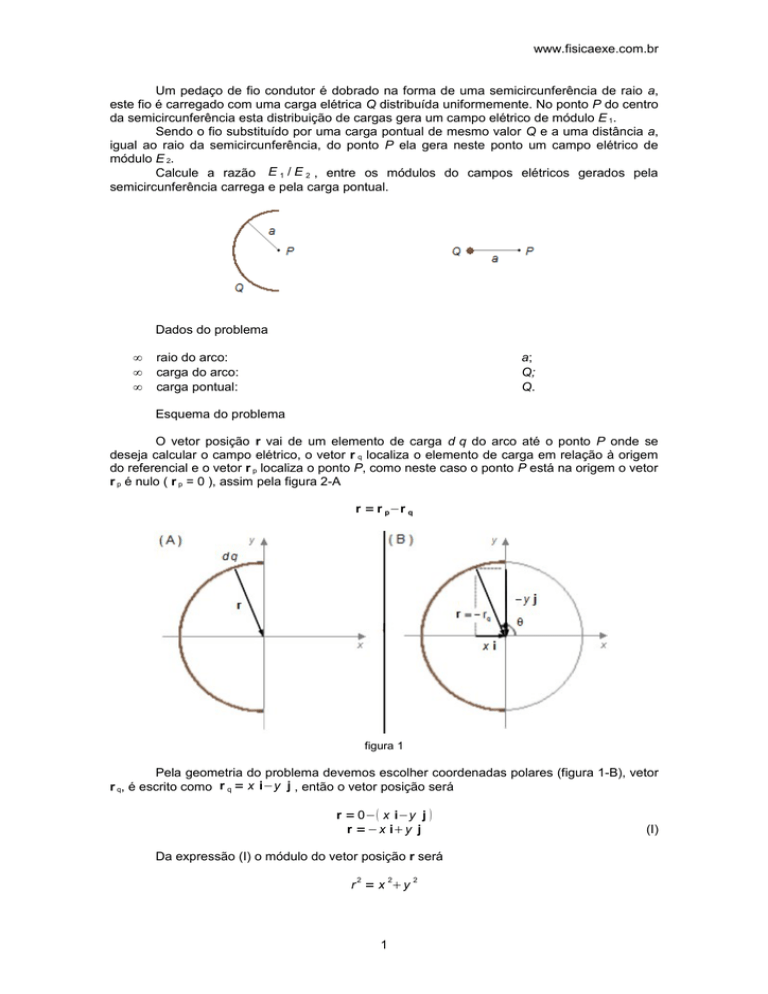
Um pedaço de fio condutor é dobrado na forma de uma semicircunferência de raio a,
este fio é carregado com uma carga elétrica Q distribuída uniformemente. No ponto P do centro
da semicircunferência esta distribuição de cargas gera um campo elétrico de módulo E 1.
Sendo o fio substituído por uma carga pontual de mesmo valor Q e a uma distância a,
igual ao raio da semicircunferência, do ponto P ela gera neste ponto um campo elétrico de
módulo E 2.
Calcule a razão E 1 / E 2 , entre os módulos do campos elétricos gerados pela
semicircunferência carrega e pela carga pontual.
Dados do problema
•
•
•
raio do arco:
carga do arco:
carga pontual:
a;
Q;
Q.
Esquema do problema
O vetor posição r vai de um elemento de carga d q do arco até o ponto P onde se
deseja calcular o campo elétrico, o vetor r q localiza o elemento de carga em relação à origem
do referencial e o vetor r p localiza o ponto P, como neste caso o ponto P está na origem o vetor
r p é nulo ( r p = 0 ), assim pela figura 2-A
r = r p−r q
figura 1
Pela geometria do problema devemos escolher coordenadas polares (figura 1-B), vetor
r q, é escrito como r q = x i−y j , então o vetor posição será
r = 0− x i−y j 
r = − x i y j
Da expressão (I) o módulo do vetor posição r será
2
2
r = x y
1
2
(I)
www.fisicaexe.com.br
r =  x 2 y 2 
1
2
(II)
onde x e y, em coordenadas polares, são dados por
x = a cosθ
,
y = a sen θ
(III)
Solução
O vetor campo elétrico do arco é dado por
1
4 π 0
1
E1=
4 π 0
∫ dr q rr
∫ dr q r
E1 =
2
(IV)
3
Da expressão da densidade linear de carga (λ) obtemos o elemento de carga d q
dq
ds
dq = ds
=
(V)
onde d s é um elemento de arco de ângulo d θ do aro (figura 2), assim
ds= a d θ
(VI)
figura 2
substituindo (VI) em (V)
dq = a dθ
(VII)
substituindo (I), (II) e (VII) em (IV), temos
E1 =
E1
1
4 π 0
 a dθ
∫
 − x iy j 
3
[  x y  ]
1
 a dθ
=
 − x iy j 
4π  ∫
2
0
x
2
2
2
y
1
2

3
2
substituindo as expressões de (III) em (VIII), vem
E1 =
1
4 π 0
∫
1
E1 =
4 π 0
 a dθ
[  a cos θ 
∫
1
E1=
4 π 0
2
  a sen θ 
 a dθ
[a
∫
E1=
[
2
cos θa sen θ ]
 a dθ
a
2
2
2
2
 cos θsen θ 

1
4 π 0
2
2
1
2
]
3
2
 −a cos θ ia sen θ j 
3
2
]
 −a cos θ ia sen θ j 
3
2
a  −cos θ i senθ j 
∫  a d θ  −cos θ isen θ j 
3
2 2
1
4 π 0
1
E1=
4 π 0
E1=
2
a
2
 a dθ
 −cos θ isen θ j 
3
a
 dθ
 −cos θ isen θ j 
a
∫
∫
2
(VIII)
www.fisicaexe.com.br
Como a densidade de carga λ e o raio a são constantes, a integral depende apenas de
θ, eles podem “sair” da integral, e sendo a integral da soma igual a soma das integrais
podemos escrever
E1 =
∫
1 
−
4 π 0 a
∫ sen θ d θ j 
cos θ d θ ia
π
3π
e
(meia volta no
2
2
Os limites de integração serão
círculo trigonométrico – figura 3)
∫
3π
2
E1 =
1 
−
4 π 0 a
3π
2
∫ sen θ d θ j
cos θ d θ i
π
2
π
2

figura 3
3π
2
integração de
∫ cos θ d θ
π
2
3π
2
∫
3π
cos θ d θ = sen θ ∣ π2 = sen
2
π
2
3π
π
−sen = −1−1 = −2
2
2
3π
2
integração de
∫ sen θ d θ
π
2
3π
2
∫
3π

sen θ d θ = −cos θ ∣ π2 = − cos
2
π
2
E1 =

3π
π
−cos
= − 0−0  = 0
2
2
1 
[ − −2  i0 j ]
4 π 0 a
1 
E1 =
i
2 π 0 a
(IX)
A carga total do arco é Q, o comprimento de uma semicircunferência é metade do
2 πa
= π a , assim a densidade linear de carga pode
componente de uma circunferência C =
2
ser escrita
=
Q
πa
substituindo (X) em (IX), temos
3
(X)
www.fisicaexe.com.br
1
Q
i
2 π 0 a π a
Q
E1=
i
2 π 2  0a 2
E1 =
e o módulo do campo elétrico será
Q
2
2 π 0 a
E1=
2
(XI)
O vetor campo elétrico gerado por uma carga pontual é
E2=
1 Q r
4 π 0 r 2 r
e seu módulo será
E2=
1 Q
4 π 0 r 2
E2=
1 Q
4 π 0 a 2
para uma distância r = a, obtemos
(XII)
A razão entre as intensidades dos campos elétricos gerados pela distribuição de cargas
numa semicircunferência e pela carga pontual é obtida dividindo-se a expressão (XI) por (XII),
assim
Q
2
E1
2 π 0 a
=
E2
1 Q
4 π 0 a 2
E1
4 π 0 a 2
Q
=
2
2
E 2 2 π 0a
1 Q
2
E1 2
=
E2 π
π
E
2 1
mais intenso (mais forte) que o campo gerado pela distribuição de da mesma carga Q numa
semicircunferência.
Observação: este resultado significa que o campo gerado pela carga pontual é E 2 =
4