Relações métricas no triângulo Qualquer

SEI Ensina ‐ MILITAR Matemática Relações métricas no triângulo Qualquer
1. (IME 2009) Um triângulo ABC apresenta lados a, b e c. Sabendo que B̂ e Ĉ são, respectivamente, os ângulos
opostos aos lado b e c, o valor de
(A)
(B)
(C)
(D)
tg B̂
tg Ĉ
é
a 2 − b 2 + c 2c
a 2 + b2 − c2b
a 2 + b2 − c2
a 2 − b2 + c2
a 2 − b2 + c2
a 2 + b2 − c2
a 2 + b 2 − c 2c
a 2 − b2 + c2b
b
(E)
c
2. (IME 2011) Seja ABC um triângulo onde α, β e γ são os ângulos internos dos vértices A, B e C, respectivamente.
Esse triângulo está inscrito em um círculo de raio unitário. As bissetrizes internas desses ângulos interceptam esse
α
β
y
AA1 cos + BB1 cos + CC1 cos
2
2
2
círculo nos pontos A1, B1 e C1, respectivamente. Determine o valor da expressão
.
sen α + sen β + sen y
3. (IME 2010) Seja x o valor do maior lado de um paralelogramo ABCD. A diagonal AC divide  em dois ângulos,
iguais a 30º e 15°. A projeção de cada um dos quatro vértices sobre a reta suporte da diagonal que não o contém forma o
quadrilátero A’B’C’D’. Calcule o perimetro de A’B’C’D’.
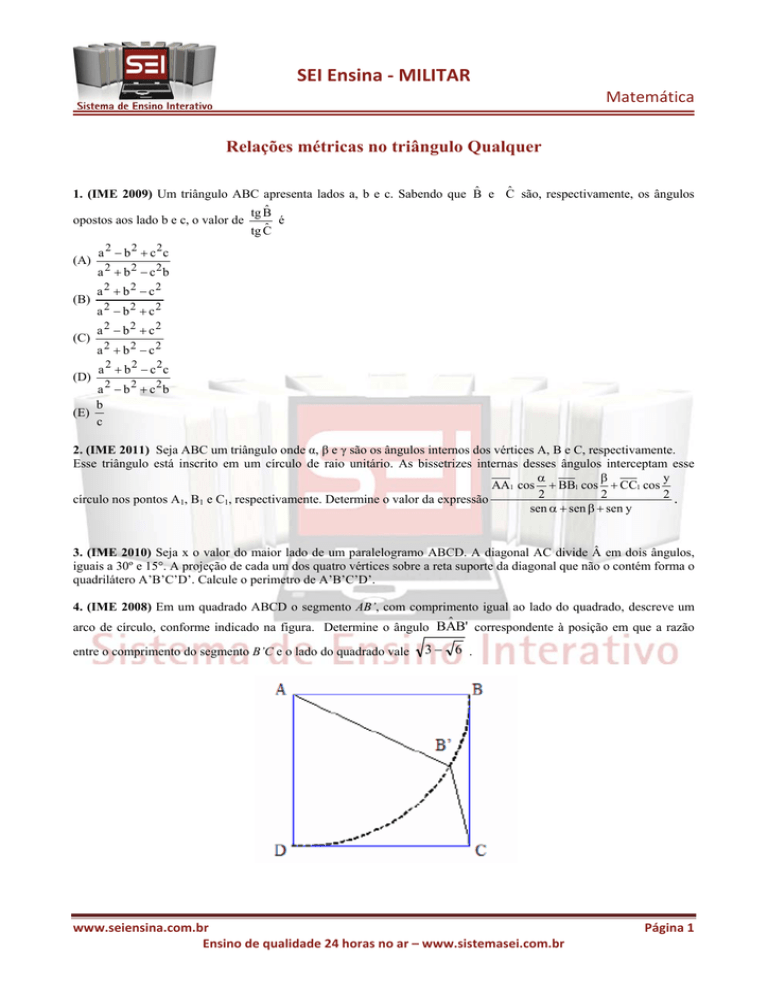
4. (IME 2008) Em um quadrado ABCD o segmento AB’, com comprimento igual ao lado do quadrado, descreve um
arco de círculo, conforme indicado na figura. Determine o ângulo BÂB' correspondente à posição em que a razão
entre o comprimento do segmento B’C e o lado do quadrado vale
3− 6 .
www.seiensina.com.br Ensino de qualidade 24 horas no ar – www.sistemasei.com.br Página 1 5. (IME 2000) As medianas BE e CF de um triângulo ABC se cortam em G. Demonstre que tg BĜC =
12 S
, onde S é a área do triângulo ABC; AC = b; AB = c e BC = a.
2
b + c 2 − 5a 2
6. (IME 1999) ABCD é um quadrado de lado A , conforme figura abaixo. Sabendo-se que K é a soma dos quadrados
das distâncias de um ponto P do plano definido por ABCD aos vértices de ABCD, determine:
(i) O valor mínimo de K e a posição do ponto P na qual ocorre este mínimo;
(ii) O lugar geométrico do ponto P para K = 4 A 2.
7. (IME 1990) Os lados de um triângulo estão em progressão aritmética e o lado intermediário mede l. Sabendo-se que
o maior ângulo excede o menor em 90º, calcule a razão entre os lados.
8. (IME 1988) Calcule o lado c de um triângulo ABC, em função de sua área S, do ângulo C e de k, onde k = a + b –
c.
9. (IME 1987) Dado um triângulo ABC de lados a, b e c opostos aos ângulos  , B̂ , Ĉ respectivamente e de
perímetro 2p, mostre que
a=
p sen
cos
Â
2
B̂
Ĉ
cos
2
2
10. (IME 1986) Num triângulo ABC (  > B̂ > Ĉ ) traçam-se as bissetrizes externas AA’ do ângulo  , com A’ sobre
o prolongamento de BC, e CC’ do ângulo Ĉ , com C’ sobre o prolongamento de AB. Se AA’ = CC’ mostre que
c sen
 − B̂
B̂ − Ĉ
= a sen
2
2
www.seiensina.com.br
Ensino de qualidade 24 horas no ar – www.sistemasei.com.br
Página 2
Gabarito:
1. B
2. 2
(
3.
2p = x
4.
15D ou 75D
)
3 + 2 −1
5. Demonstração
6. (i) Centro do quadrado (ii) Circunferência de Centro no centro do quadrado e R = l 2
7.
r=
8.
c=
l 7
7
2S (1 + cos C )
k sen C
−
k
2
9. Demonstração
10. Demonstração
www.seiensina.com.br
Ensino de qualidade 24 horas no ar – www.sistemasei.com.br
Página 3