Ciclo trigonométrico com os arcos notáveis – de 0º a 360º 1

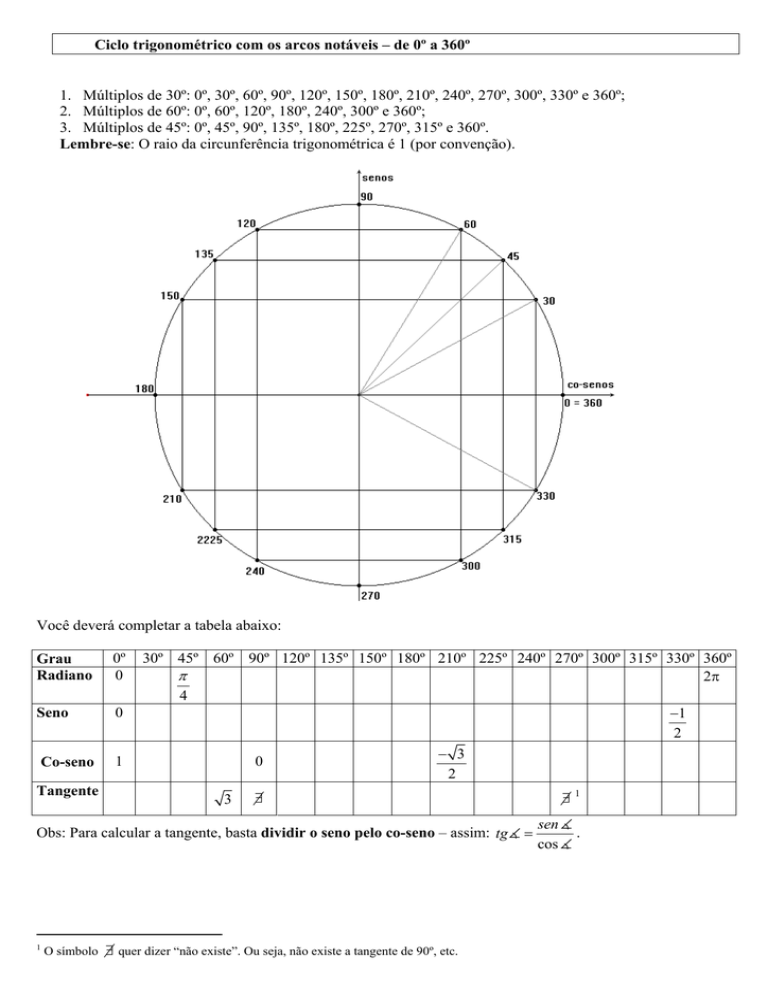
Ciclo trigonométrico com os arcos notáveis – de 0º a 360º
1. Múltiplos de 30º: 0º, 30º, 60º, 90º, 120º, 150º, 180º, 210º, 240º, 270º, 300º, 330º e 360º;
2. Múltiplos de 60º: 0º, 60º, 120º, 180º, 240º, 300º e 360º;
3. Múltiplos de 45º: 0º, 45º, 90º, 135º, 180º, 225º, 270º, 315º e 360º.
Lembre-se: O raio da circunferência trigonométrica é 1 (por convenção).
Você deverá completar a tabela abaixo:
Grau
Radiano
0º
0
Seno
0
Co-seno
1
Tangente
30º 45º 60º 90º 120º 135º 150º 180º 210º 225º 240º 270º 300º 315º 330º 360º
π
2π
4
−1
2
− 3
0
2
3
∃
Obs: Para calcular a tangente, basta dividir o seno pelo co-seno – assim: tg ( =
1
O símbolo ∃ quer dizer “não existe”. Ou seja, não existe a tangente de 90º, etc.
∃1
sen (
.
cos (
3
3
sen 60º
Exemplo: tg 60º =
= 2 =
= 3
1
cos 60º
1
2
Funções trigonométricas
Seno de um arco: Associando cada nº real x a um arco p
AP da circunferência trigonométrica, com origem no
ponto A(0,1) e extremidade em um ponto P tal que med( p
AP ) = x rad, dizemos que o seno do arco x é a
ordenada OP1 do ponto P.
Função seno: É a função f: R → R que, a cada número real x, associa o seno desse número:
f: RÆ R
x Æ y = f(x) = sen x
(leia-se: f de x é igual a seno de x)
O domínio dessa função é o conjunto \ , e a imagem é Im = [-1, 1].
Sinal da função seno:
Como o seno de x é a ordenada do pontoextremidade do arco, A função
•
•
y = sen x é positiva no 1º e 2º quadrantes; e
y = sen x é negativa no 3º e 4º quadrantes.
Exercício 1: Calcule os valores de: sen 0, sen
π
2
, sen π , sen
3π
e sen 2π . (Veja a figura a seguir)
2
Exercício 2: Determine os sinais de: sen 30º, sen 130º, sen 220° e sen 330º.
Gráfico da função seno (y = sen x)
Para se construir o gráfico da função seno, você deve localizar inicialmente, na circunferência
trigonométrica, alguns arcos e determinar o valor dos seus senos.
Marcando esses valores no Plano cartesiano, vamos construir o gráfico da função y = sen x.
p
AP da circunferência trigonométrica, com origem
no ponto A(0,1) e extremidade em um ponto P tal que med( p
AP ) = x rad, dizemos que o co-seno do arco x é a
abscissa OP2 do ponto P.
Co-seno de um arco: Associando cada nº real x a um arco
Função co-seno: É a função f: ℜ → ℜ que, a cada número real x, associa o co-seno desse número:
f:
\Æ \
x
6y
= f(x) = cos x
(leia-se: f de x é igual a co-seno de x)
O domínio dessa função é o conjunto ℜ , e a imagem é Im = [-1, 1].
Sinal da função co-seno:
Como o seno de x é a ordenada do ponto-extremidade do arco, a função
•
•
y = cos x é positiva no 1º e 4º quadrantes; e
y = cos x é negativa no 2º e 3º quadrantes.
Ex. 3) Calcule os valores de: cos 0, cos
π
2
, cos π , cos
3π
e cos 2π .
2
Ex. 4) Determine os sinais de: cos 30º, cos 120º, cos 210º, cos 300º e cos 900º. Veja a figura abaixo, em que
está resolvido o cos 900º.
Ex.5) Calcule o valor da expressão
cos
π
3
+ cos 2π + cos
2π
.
3
Gráfico da função cos-seno (y = cos x)
Para construir o gráfico da função co-seno, nós devemos, inicialmente, localizar na circunferência
trigonométrica, alguns arcos e, em seguida, determinar o valor do seu co-seno.
Marcando esses valores no plano, construímos o gráfico da função y = cos x.
É fácil ver que os valores do 1º quadrante são simétricos em relação aos do 4° quadrante, e os valores do 2º
quadrante são simétricos aos do 3º.
Exercício 6) Esboce os gráficos das funções seno de x e co-seno de x (y = sen x e y = cos x).
Ex.7) Dê o valor de:
Ex.8) Calcule o valor de:
Ex.9) Dê o valor de:
Ex. 9) Trace os gráficos de: a) y = cos 2x
b) y = cos x/2
c) y = sen 2x
d) y = sen x/2