Tecnologia digital Trabalho nº 2

Tecnologia digital
Trabalho nº 2 – Somador aritmético completo
Introdução:
Qualquer sistema de processamento deve ser capaz de executar operações aritméticas
básicas, as quais podem ser combinadas em funções mais complexas.
A função de adição pode ser utilizada na execução das operações subtração,
multiplicação e divisão.
Portanto, o circuito somador é o núcleo da maioria das unidades aritméticas.
Genericamente, um somador completo além de adicionar os 2 bits referentes aos
operandos também adiciona um bit de transporte (carry) proveniente de uma coluna
anterior.
Objetivos gerais:
Montar e testar um primeiro circuito somador completo de dois números de 1 bit.
Montar e testar um segundo circuito somador completo de dois números de 1 bit.
Montar e testar um somador completo de dois números de 2 bits.
Objetivo específico:
Confirmar o resultado da soma de dois números de 2 bits.
Material necessário
- Fonte de alimentação regulada (×1);
- protoboard (×1);
- 74LS00: CI com quatro portas NAND de duas entradas (×3);
- 74LS86: CI com quatro portas XOR de duas entradas (×1);
PIN-out dos CIs 74LS00 e 74LS86
Especificações de um somador completo de dois números de 1 bit
O núcleo deste trabalho passa pelo projeto de um circuito lógico combinacional que
implemente dois somadores completos (full adder) de dois números de 1 bit, cujos sinais
de saída são:
- o resultado da soma de dois números de 1 bit: S=S(X,Y,Cin)
- o transporte resultante da soma de dois números de 1 bit: Cout= Cout(X,Y,Cin).
Um somador completo pode ser implementado através da interconexão de dois meio
somadores.
A figura 1 ilustra o diagrama de blocos de um meio somador, enquanto a tabela de
verdade mostra a representação funcional das funções S e C.
Figura 1 – Circuito Meio Somador
A figura 2 ilustra o diagrama de blocos de um full-adder, enquanto a tabela de verdade
mostra a representação funcional das funções S e Cout.
Figura 2 – Circuito Somador Completo
Na função full-adder, as variáveis X e Y são os operandos de 1 bit (números de 1 bit a
somar) e Cin é o transporte resultante da soma à esquerda.
Implementar dois somadores completos conforme o diagrama de blocos abaixo:
A2
Cout2
B2
full-adder
A1
Cin2
Cout1
B1
full-adder
Cin1 =0
GND
S2
S1
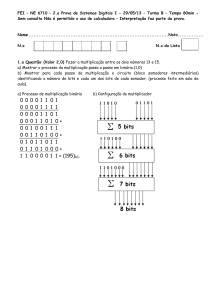
(15) Preencher a tabela seguinte com os resultados experimentais.
A2A1
B2B1
S2S1
A2 A1
B2 B 1
S2 S 1
(decimal)
(decimal)
(decimal)
0
0
0
0
0
0
0
1
1
0
0
0
1
0
2
0
0
0
1
1
3
0
0
0
0
0
0
0
1
1
0
1
1
0
1
1
1
0
2
0
1
1
1
1
3
0
1
1
0
0
0
1
0
2
0
1
1
1
0
2
1
0
2
1
0
2
1
1
3
1
0
2
0
0
0
1
1
3
0
1
1
1
1
3
1
0
2
1
1
3
1
1
3
1
1
3
Que conclusões se retiram da tabela anterior?
Cout2