Matemática 2 (2006)

Matemática 2
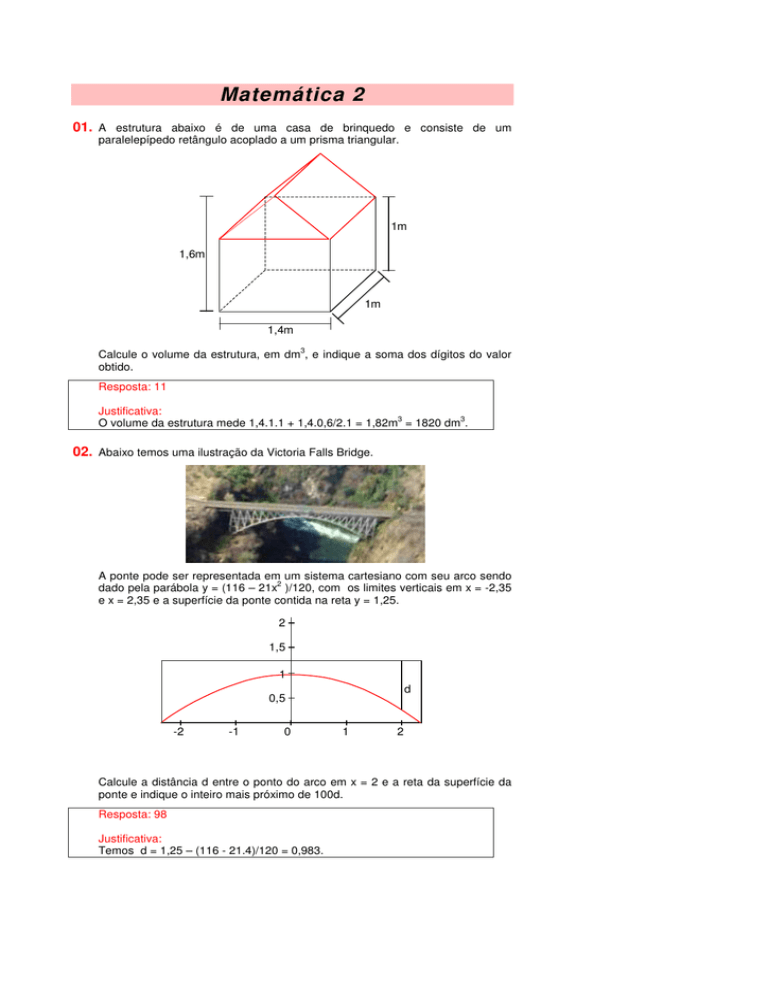
01. A estrutura abaixo é de uma casa de brinquedo e consiste de um
paralelepípedo retângulo acoplado a um prisma triangular.
1m
1,6m
1m
1,4m
3
Calcule o volume da estrutura, em dm , e indique a soma dos dígitos do valor
obtido.
Resposta: 11
Justificativa:
3
3
O volume da estrutura mede 1,4.1.1 + 1,4.0,6/2.1 = 1,82m = 1820 dm .
02. Abaixo temos uma ilustração da Victoria Falls Bridge.
A ponte pode ser representada em um sistema cartesiano com seu arco sendo
2
dado pela parábola y = (116 – 21x )/120, com os limites verticais em x = -2,35
e x = 2,35 e a superfície da ponte contida na reta y = 1,25.
2
1,5
1
d
0,5
-2
-1
0
1
2
Calcule a distância d entre o ponto do arco em x = 2 e a reta da superfície da
ponte e indique o inteiro mais próximo de 100d.
Resposta: 98
Justificativa:
Temos d = 1,25 – (116 - 21.4)/120 = 0,983.
03. As cidades A , B e C estão localizadas de modo que: a cidade B está a uma
o
distância de 60km de A, na direção de 29 , e a cidade C está a uma distância
o
de 80km de A, na direção de 89 . Calcule a distância entre B e C, em km, e
indique o inteiro mais próximo do valor obtido.
C
B
89º
29º
A
Resposta: 72
Justificativa:
2
2
A distância entre B e C é dada pela Lei dos cossenos: (60 + 80 –
1/2
1/2
2.60.80.1/2) = 5200 ≅ 72,11.
04. Na ilustração abaixo, o paralelepípedo retângulo foi cortado por um plano
perpendicular a sua base e ficou dividido em dois sólidos.
2
5
4
3
4
3
Calcule os volumes dos sólidos obtidos e indique o valor do maior.
Resposta: 48
Justificativa:
Os volumes medem 3.4.3 = 36 e 3.4.4 = 48.
05. Determine o valor de x para os quais os pontos (2x + 3, x – 5), (2x + 4, 2x - 12)
e (3x – 3, 2x – 11) são distintos e colineares.
Resposta: 8
Justificativa:
Os pontos serão colineares se e só se [(2x -12) - (x – 5)]/[(2x + 4) – (2x +
3)] = [(2x – 11) – (2x – 12)]/[(3x – 3) – (2x + 4)] ou (x - 7)/1 = 1/(x – 7). Daí
2
(x – 7) = 1 e x = ±1 + 7 = 8 ou 6. Para x = 6, o primeiro e o terceiro
pontos dados coincidem.
06. Na ilustração a seguir, as seis circunferências menores têm mesmo raio e são
tangentes internamente à circunferência maior. Além disso, cada uma das
circunferências menores é tangente às duas outras que lhe são adjacentes.
Dado que as circunferências menores têm raio 2, calcule a área da região
colorida e indique o inteiro mais próximo do valor obtido.
Dado: use a aproximação π ≅ 3,14.
Resposta: 38
Justificativa:
O centro da circunferência maior e os centros de duas circunferências
menores e adjacentes são vértices de um triângulo isósceles com ângulo
o
da base medindo 60 , logo este triângulo é eqüilátero. Se r é o raio da
circunferência maior então o triângulo mencionado tem lados r – 2, r – 2 e
2
2
2.2, portanto r = 6. A área da região procurada é π6 - 6π2 = 12π ≅
37,68.
07. O polígono estrelado a seguir é tal que os triângulos construídos tendo por
bases os lados do pentágono, que estão pontilhados, são isósceles e
congruentes. Assinale a medida, em graus, do ângulo do vértice destes
triângulos.
(Note que cada reta contendo um lado do pentágono contém dois lados do
polígono estrelado.)
Resposta: 36
Justificativa:
O pentágono no interior da figura tem lados congruentes e ângulos
internos congruentes, logo é regular. Os ângulos internos do pentágono
o
o
medem (5 - 2).180 /5 = 108 , portanto o ângulo do vértice dos triângulos
o
o
o
isósceles mede 180 – 2.72 = 36 .
08. A ilustração abaixo é de um design encontrado em Pompéia e consiste de um
hexágono regular, seis quadrados, seis losangos, seis triângulos equiláteros e
doze triângulos retângulos.
Se o lado do hexágono é 2 indique o inteiro mais próximo da área da figura.
Dado: use a aproximação: 3 ≅ 1,7 .
Resposta: 89
Justificativa:
Os lados do hexágono, quadrados, losangos e triângulos eqüiláteros têm
mesma medida, assim como os catetos dos triângulos retângulos.
Observe que os losangos podem ser divididos em dois triângulos
eqüiláteros. Portanto, a área da figura é
(6 + 12 + 6)2
2
2
3 /4 + 6.2 + 12.2.2/2 = 24(1,7 + 2) = 88,8.
As informações abaixo referem-se às duas questões a seguir:
Em um cone reto com raio da base 20cm e altura 60cm, está inscrito um
cilindro reto, como ilustrado a seguir.
09. Qual deve ser a altura do cilindro, em cm, de modo que a área total da sua
superfície seja máxima?
Resposta: 15
Justificativa:
Sejam r e h o raio da base e a altura respectivos do cilindro inscrito.
2
Temos que a área total do cilindro é dada por A = 2πrh + 2πr . De
semelhança de triângulos obtemos r/20 = (60 – h)/60 e daí h = 60 – 3r. A
2
área se expressa como A = 2πr(60 – 3r) + 2πr = 2πr(60 – 2r). A área do
cilindro será máxima quando r = (0 + 30)/2 = 15cm e h = 15cm.
10. Calcule o volume V, em cm3, do cilindro, com área total de sua superfície
máxima e inscrito no cone. Indique V/(45π).
Resposta: 75
Justificativa:
2
3
3
Temos V = πr h = π15 cm e V/(45π) = 75.
As informações abaixo referem-se as duas questões a seguir.
Na ilustração seguinte, temos um tetraedro ABCD com base BCD inscrita em
uma circunferência. A aresta AB do tetraedro é perpendicular ao plano
contendo a circunferência e BD é um diâmetro da circunferência. As medidas
de AB, BD e CD são, respectivamente, 35cm, 13cm e 5cm.
A
B
D
C
11. Calcule a medida de AC, em cm, e assinale o valor obtido.
Resposta: 37
Justificativa:
Considerando que BD é um diâmetro temos que o triângulo BCD é
2
2 1/2
retângulo em C e que BC mede ( 13 - 5 ) = 12cm. Da mesma maneira
2
2 1/2
AC = (12 + 35 ) = 37cm.
12. Calcule o volume do tetraedro, em cm3, e indique a soma dos dígitos do
número obtido.
Resposta: 8
Justificativa:
3
O volume do tetraedro é (12.5/2).35/3 = 350cm .
13. Os naturais 26.3m.54 e 2p.37.5n têm máximo divisor comum 26.36.54 e mínimo
8
7
4
múltiplo comum 2 .3 .5 . Calcule os naturais m, n e p e indique sua soma.
Resposta: 18
Justificativa:
Temos que o maior entre 6 e p é 8, logo p = 8. O menor entre m e 7 é 6,
logo m = 6. O menor e o maior entre 4 e n são iguais a 4, logo n = 4.
14. A figura abaixo ilustra um antigo símbolo gótico.
A circunferência maior tem raio 24, as duas circunferências intermediárias, que
são tangentes a maior, têm raio 12 e as cinco circunferências menores têm raio
6. Quatro das circunferências menores têm diâmetros que, reunidos, formam
um diâmetro da circunferência maior que também contém um diâmetro de uma
das circunferências intermediárias. A quinta circunferência menor é tangente a
duas das circunferências menores. A outra circunferência intermediária passa
pelo centro da primeira e pelo centro da maior. Calcule o comprimento C do
contorno destacado e assinale C/π.
Resposta: 38
Justificativa:
o
O contorno é formado de três arcos de 300 contidos em uma circunferência
o
de raio 6 e um arco de 120 de uma circunferência de raio 12, logo, mede
3.300/360.2.π.6 + 120/360.2.π.12 = 30π + 8π = 38π.
15. A figura abaixo ilustra o cuboctaedro truncado, que é um poliedro convexo com
12 faces quadradas, 8 hexagonais e 6 octogonais. Quantos são seus vértices?
Resposta: 48
Justificativa:
O número de arestas do poliedro é (12.4 + 8.6 + 6.8)/2 = 72 e seu
número de vértices é 72 – (12 + 8 + 6) + 2 = 48.
16. Um robô encontra-se na origem de um reta com coordenadas e pode mover-se
sobre a reta, em passos de comprimento 1, para a direita ou para a esquerda.
Se a probabilidade do robô mover-se para a direita é de 2/5, qual a
probabilidade percentual p% de ele se encontrar na posição –1, após executar
três passos? Indique o inteiro mais próximo de p.
Resposta: 43
Justificativa:
As possíveis trajetórias para o robô sair da posição 0 e, depois de três
passos, encontrar-se na posição -1 são EED, EDE e DEE (onde E e D
denotam movimentos para a esquerda e direita, respectivamente). A
probabilidade procurada é 3.3/5.3/5.2/5 = 54/125 e daí p = 54.100/125 =
= 43,2%.
17. As arestas do sólido convexo ilustrado a seguir são obtidas unindo os pontos
médios de cada uma das arestas de um tetraedro regular aos pontos médios
das quatro arestas que são concorrentes com ela.
Se aresta do tetraedro mede 6
2 , qual o volume do sólido?
Resposta: 36
Justificativa:
O sólido é um octaedro regular com aresta medindo 3
é 2. (3
2 . O seu volume
2
2 ) 3/3 = 36.
18. Os círculos na ilustração a seguir têm raios 10 e 14 e são secantes. Qual a
diferença d entre a medida da área da região do círculo maior, sem pontos do
círculo menor, e a medida da área da região do círculo menor, sem pontos do
círculo maior? Indique d/π.
Resposta: 96
Justificativa:
Se a medida da área da região do círculo maior sem pontos do círculo
menor é x, a medida da área da região do círculo menor sem pontos do
círculo maior é y e a medida da área comum aos dois círculos é z, temos
2
2
que a diferença procurada é d = (x + z) – (y + z) = x – y = π14 - π10 =
96π.
19. Cinco cidades são vértices de um pentágono convexo e devem ser conectadas
por quatro rodovias retilíneas (que podem se interceptar). As rodovias serão
construídas de modo que exista um trajeto unindo quaisquer duas destas
cidades. Abaixo temos as três maneiras básicas de se construir tais rodovias:
na primeira, de cada cidade saem no máximo duas rodovias; na segunda,
existe uma cidade de onde saem três rodovias e, na terceira, existe uma cidade
de onde saem quatro rodovias.
Determine o número total de maneiras de se construir as quatro rodovias e
assinale a soma dos seus dígitos.
Resposta: 8
Justificativa:
Do primeiro tipo, o número de maneiras de construir as rodovias é 5!/2 =
120/2 = 60; do segundo tipo, temos 5.4.3 = 60 maneiras e do terceiro
temos 5 maneiras. O total de maneiras de construir as rodovias é 60 +
60 + 5 = 125 maneiras.
20. Existem duas circunferências situadas no primeiro quadrante que são tangentes
aos eixos das abscissas e das ordenadas e tangentes à reta com equação 5x
+ 12y – 60 =0. Determine os raios das circunferências e indique sua soma.
Resposta: 17
Justificativa:
Desde que as circunferências são tangentes aos eixos coordenados e
estão no primeiro quadrante temos que seus centros têm coordenadas
(r, r), com r sendo o raio das circunferências. Como a reta 5x + 12y –
60 =0 é tangente às circunferências temos |5r + 12r – 60|/ 52 + 122 = r
ou |17r – 60| = 13r que eqüivale a 17r – 60 = ±13r, que tem soluções r
= 15 e r = 2.
21. A seguir temos uma ilustração da Grande Pirâmide do Egito.
h
H
2a
A pirâmide é regular e o quadrado da sua altura é igual ao produto da metade
do lado da base pela altura dos triângulos das faces, ou seja, se 2a é o lado da
base da pirâmide, h a sua altura e H a altura dos triângulos das faces laterais
2
4
temos h = H(2a)/2 = Ha. Calcule g = H/a e indique (2g – 1) .
Resposta: 25
Justificativa:
2
2
2
2
2
Temos H = h + a = Ha + a e daí (H/a) – (H/a) –1 = 0. Resolvendo a
equação obtemos H/a = (1 ±
4
1) = 25.
5 )/2 e segue que g = (1 +
5 )/2 e (2g –
22. O prisma pentagonal ilustrado abaixo é regular, com lado da base medindo
400/17 e altura medindo 42. Determine o raio da esfera circunscrita ao prisma
e indique o inteiro mais próximo do valor obtido.
o
Dado: use a aproximação cos(54 ) ≅ 10/17.
Resposta: 29
Justificativa:
Seja x a medida do lado do triângulo isósceles com vértice no centro da
o
base do prisma e base em um lado da base do prisma. Temos cos(54 ) =
(200/17)/x e x ≅ (200/17)/(10/17) = 20. O raio da esfera circunscrita é
2
2 1/2
1/2
(20 + 21 ) = 841 = 29.
23. Júnior comprou um certo número de chocolates (iguais) por R$ 20,25. Se o
preço de cada chocolate fosse R$ 0,02 a menos, ele teria obtido 6 chocolates a
mais. Quantos chocolates Júnior comprou?
Resposta: 75
Justificativa:
Se o preço pago foi de p centavos por chocolate, e Júnior comprou n
chocolates, temos 2025 = pn = (p - 2)(n + 6) e da segunda igualdade
resulta que pn = pn + 6p –2n –12 que se simplifica como n = 3(p – 2).
Substituindo na primeira igualdade, com 2025 fatorado em primos, temos
4 2
3 2
3 .5 = 3p(p – 2) ou 3 .5 = p(p – 2). Como p é ímpar temos p e p – 2
3
2
primos entre si e daí p = 3 = 27 centavos e n = 3.5 = 75.
24. A figura abaixo ilustra a divisão de um hexágono regular em três triângulos um
quadrilátero e um pentágono, que são rearrumados para formar um quadrado.
α
2
Se α é a medida do ângulo indicado, escreva sen α =
naturais, a primo, e indique a + b.
a / b com a e b
Resposta: 9
Justificativa:
Se l é a medida do lado do hexágono regular então sua área é dada por
3l
2
2
3 /2 e o quadrado que tem a mesma área do hexágono tem lado
1/2
(3l 3 /2) . O triângulo acutângulo da dissecção tem um ângulo
o
medindo 120 , outro medindo α, e os lados opostos a estes ângulos
medem (3l
2
3 /2)
1/2
e l, respectivamente. Usando a lei dos senos,
obtemos (3l
2
1/2
o
3 /2) /sen 120 = l/sen α e sen α = ( 3 /2)/(3 3 /2)
1/2
2
( 3 /2) / 3 e sen α =
1/2
=
3 /6. Daí a = 3 e b = 6.
25. Uma formiga move-se ao longo das arestas de um cubo e, encontrando-se,
inicialmente, no vértice A, deverá se mover até o vértice B (veja a ilustração a
seguir). Ao percorrer uma aresta, a formiga não muda o sentido do trajeto até
atingir o outro vértice da aresta. Se a formiga escolhe seu trajeto
aleatoriamente, qual a probabilidade percentual p% de ela atingir o vértice B,
após caminhar o equivalente ao comprimento de três arestas do cubo? Indique
o inteiro mais próximo de p.
B
A
Resposta: 22
Justificativa:
O número de trajetórias de A até B usando três arestas é 3.2.1 = 6 e o
número total de trajetórias usando três arestas não necessariamente
distintas é 3.3.3 = 27, logo a probabilidade procurada é 6/27 = 2/9 ou
22,22%
26. Suponha que as diagonais de um octógono convexo, ou não se interceptam no
interior do octógono, ou se interceptam, duas a duas, em pontos distintos.
Quantos são estes pontos de interseção, situados no interior do octógono?
Resposta: 70
Justificativa:
Cada par de diagonais, que se interceptam no interior do octógono,
corresponde às diagonais de um quadrilátero com vértices com vértices
nos extremos das diagonais (logo, em vértices do octógono).
Reciprocamente, cada quatro vértices do octógono determinam um
quadrilátero convexo cujas diagonais são diagonais do octógono e se
interceptam em um ponto de seu interior. Portanto, o número de pontos
de interseção das diagonais do octógono, que estão em seu interior,
corresponde ao número de maneiras de se escolher quatro pontos de um
conjunto de oito, que vale 8.7.6.5/(4.3.2.1) = 70.
27. Um depósito na forma de um paralelepípedo retângulo está preenchido com
certo volume de líquido. Ao colocarmos no interior do paralelepípedo um cubo
sólido de aresta 4cm, com densidade maior que a do líquido, a altura do líquido
fica igual à aresta do cubo. O paralelepípedo tem base com comprimento 5cm e
largura 6cm. Determine a aresta x de outro cubo sólido, com densidade maior
que a do líquido, que, quando colocado no interior do paralelepípedo, deixa a
2
altura do líquido igual à medida da aresta. Indique (x + 2) .
Resposta: 18
Justificativa:
3
Temos que o volume de líquido no paralelepípedo é 5.6.x – x , logo, 30x
3
3
3
3
– x = 30.4 – 4 , que se simplifica como x – 4 – 30x +30.4 = 0.
2
Colocando x – 4 em evidência temos (x - 4)(x + 4x +16) –30(x – 4) = 0
2
2
ou (x – 4)(x + 4x – 14) = 0. Como queremos x ≠ 4 temos x + 4x – 14 = 0
e x = (-4 ±
72 )/2 = -2 ± 3 2 . Uma vez que x é positivo temos x = -2
2
+3 2 e (x + 2) = 18.
28. Um triângulo isósceles ABC tem ângulos da base AB medindo o dobro do
ângulo do vértice C, como ilustrado a seguir.
C
D
A
B
O segmento AD é a bissetriz do ângulo CAB. Analise as afirmações a seguir,
referentes ao triângulo ABC.
o
0-0) O ângulo ACB mede 36
1-1) Os triângulos ABC e BDA são semelhantes.
2-2) O triângulo ADC é isósceles.
3-3) AB/AC = (-2+ 5 )/2
4-4) A razão entre as áreas do triângulo ABC e do triângulo BDA é (3 +
Resposta: VVVFV
5 )/2
Justificativa:
o
Se α é a medida do ângulo ACB temos α + 2α + 2α = 180 e daí α =
o
º
180 /5 = 36 , logo 0-0) é verdadeira. Pelo teorema do ângulo externo
temos que a medida do ângulo ADB é 2α, portanto os triângulos ABC e
BDA são semelhantes e 1-1) é verdadeira. O triângulo ADC tem ângulos
DCA e DAC medindo α, logo é isósceles, e 2-2) é verdadeira. Da
semelhança entre ABC e BDA temos AB/AC = (AC – AB)/AB, que se
2
2
simplifica como AB + AC.AB – AC = 0 e daí AB = (-1 ±
AB/AC = (-1 +
5 )AC/2 e
5 )/2, logo 3-3) é falsa. A razão entre as áreas dos
triângulos ABC e BDA é [2/(-1 +
4-4) é verdadeira.
2
5 )] = 2/( 3 - 5 ) = (3 +
5 )/2, logo
29. A figura abaixo ilustra um paralelepípedo retângulo desenhado em papel
quadriculado. Analise as afirmações abaixo, referentes as posições relativas
dos pontos A, B, C e D.
C
A
B
D
0-0) A reta contendo A e B e a reta contendo C e D são concorrentes.
1-1) O plano contendo A, B e D também contém C.
2-2) A reta contendo A e C e a reta contendo B e D são paralelas.
3-3) O plano contendo A, C e D também contém B.
4-4) Os pontos A, B, C e D são coplanares.
Resposta: FFFFF
Justificativa:
O único plano contendo A, B e D intercepta o paralelepípedo em um
retângulo que não contém C , logo, C não está no plano contendo A, B e
D e os pontos A, B, C e D não são coplanares. Portanto, 0-0), 1-1), 2-2),
3-3) e 4-4) são falsas.
30. As cidades de uma planície estão, duas a duas, situadas a distâncias
diferentes. Sejam A, B e C cidades da planície e suponha que A é a cidade
mais próxima de B e de C.
A
B
C
Analise a veracidade das afirmações a seguir, admitindo as informações acima.
0-0) BC > AB
1-1) AC > BC
2-2) O ângulo com vértice em B tem medida maior que as medidas dos
ângulos com vértices em A e C.
º
3-3) O ângulo com vértice em A mede mais de 60 .
4-4) O número de cidades que têm a cidade A como a mais próxima é menor
que 6.
Resposta: VFFVV
Justificativa:
BC é maior que AB e AC pois A é a cidade mais próxima de B e de C,
logo 0-0) é verdadeira e 1-1) é falsa. Como BC é o maior lado do
triângulo escaleno ABC, temos que o ângulo com vértice em A é o ângulo
de maior medida do triângulo, logo 2-2) é falsa. Temos  + ^B + ^C =
o
o
º
180 , ^B < Â, ^C <  e portanto 3 > 180 e  > 60 e 3-3) é verdadeira.
Se existissem pelo menos seis cidades tendo A como cidade mais
próxima, então a soma dos ângulos com vértices em A, construídos
o
o
como acima, seria maior que 6.60 = 360 , o que não pode ser.
31. A temperatura em uma sala, ao longo do dia, é dada, em oC, pela função
T(t) = 6cos(π(t - 13)/12) + 31
onde t é o número de horas após zero hora. Nestas condições, analise as
afirmações abaixo.
0-0)
1-1)
2-2)
3-3)
o
A temperatura na sala às cinco horas da tarde é de 34 C.
A temperatura da sala é máxima às 13h.
o
O menor valor da temperatura da sala é 31 C.
o
O gráfico da temperatura T (em C), em termos do número de horas t após
zero hora, é
4-4) A temperatura da sala é mínima às três horas da manhã.
Resposta: VVFFF
Justificativa:
o
Às cinco horas da tarde temos t = 17h e T(17) = 6cos(π/3)+31 = 34 C,
logo 0-0) é verdadeira. A temperatura da sala é máxima quando cos(π(t 13)/12)=1 ou π(t - 13)/12=2kπ, k inteiro, que eqüivale a t = 13 + 24k e,
como t varia de 0h a 24h, temos t = 13h, e 1-1) é verdadeira. A
temperatura é mínima Quando cos(π(t - 13)/12) = -1, ou seja, o valor
o
mínimo da temperatura é –6 + 31 = 25 C, logo 2-2) é falsa. 3-3) é falsa
o
pois o valor máximo da temperatura é 6 + 31 = 37 C, o que não ocorre
com o gráfico apresentado. A temperatura é mínima quando cos(π(t 13)/12) = -1, ou seja, quando π(t - 13)/12 = -π + 2 kπ, com k inteiro, que
se simplifica como t = 1 + 24k e t =1h, logo 4-4) é falsa.
32. Os catetos de um triângulo retângulo têm medidas que se expressam na forma
2
2n e n – 1, para algum natural n, n > 1. Analise a veracidade das afirmações a
seguir, referentes a este triângulo.
2
0-0) A hipotenusa do triângulo mede n + 1.
3
1-1) A área do triângulo é n – n.
2
2-2) O perímetro do triângulo é n + n.
3-3) O raio da circunferência inscrita no triângulo mede n + 1.
2
4-4) O raio da circunferência circunscrita ao triângulo mede n /2+1.
Resposta: VVFFF
Justificativa:
O teorema de Pitágoras assegura que a hipotenusa do triângulo mede
2
2
2
2
(2n) + (n2 − 1) = n4 + 2 n2 + 1 = (n2 + 1) = n + 1, logo 0-0) é
2
3
verdadeira. A área do triângulo mede (2n)(n – 1)/2 = n – n, portanto 1-1)
2
2
2
é verdadeira. O perímetro do triângulo mede 2n + n – 1 + n + 1 = 2(n +
n) e , portanto, 2-2) é falsa. O raio da circunferência inscrita no triângulo
3
2
mede (n – n)/(n + n) = n – 1 e, daí, 3-3) é falsa. O raio da circunferência
2
circunscrita ao triângulo mede (n + 1)/2 e, portanto, 4-4) é falsa.