Enviado por
toquecorpinturas
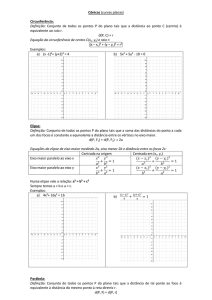
Definição de cônica

AIRTON LEANDRO DA SILVA 337302816067 JOÃO OSNILDO FERREIRA 342896816067 LEOMAR ZEFINO SOARES 278314216066 Definição de cônica. Denomina-se cônica o lugar geométrico dos pontos de um plano cuja razão entre as distâncias a um ponto fixo F e a uma reta fixa "d" é igual a uma constante não negativa “e”. O ponto fixo F é chamado de foco, a reta fixa d de diretriz e a razão constante ”e” de excentricidade da cônica. - Se e = 1, a cônica é uma parábola. - Se e < 1, a cônica é uma elipse. - Se e > 1, a cônica é uma hipérbole. Demonstração: Se e = 1, a proposição acima é a própria definição da parábola. Vamos considerar o caso em que e > 0 e e≠1. Sem perda de generalidade podemos considerar o foco F = (c, 0) e a diretriz como sendo a reta d : x = . Assim, o conjunto dos pontos P = (x,y), tais que, Pode ser calculado como: Elevando ao quadrado e simplificando, obtemos: Que ainda pode ser escrito como: Comparando com a equação da elipse E da hipérbole Vemos que se 0 < e < 1, temos uma elipse e se e > 1, temos uma hipérbole. Observe, também, que. Exemplo de Gráficos das cônicas: Relacionando os pontos da parábola a seu foco e sua diretriz. Observemos o ponto F e a reta I, diz-se que os mesmos são o foco e a diretriz da parábola quando se estabelece a relação PF=PQ. Parábola, foco e diretriz. Neste gráfico a distância focal é 2e e F1P1 + F2P1 é constante para todos os pontos do gráfico da elipse. Os pontos S1 e S2 são os vértices da elipse, enquanto que S3 e S4 são os pontos de menor raio. Os parâmetros de uma elipse. Duas hipérboles sobrepostas no mesmo gráfico, mostrando a alternância de direções pelo ajuste dos valores dos seus parâmetros. Considerando a relação de simetria dos pontos em relação aos dois pontos, podemos verificar que: |F2P| - |F1P|= ±K Note que, ao definirmos as distâncias como referência, devemos assegurar que os seus valores sejam absolutos e depois estabelecer o sinal correto para a constante em cada caso. Quando estabelecemos os valores das constantes podemos fazer com que: e2= a2 + b2 Esta relação pode ser facilmente visualizada observando-se o gráfico abaixo: A hipérbole x2 – y2=1 com parâmetros destacados, mostrando a relação entre os mesmos. Observe que os parâmetros: a, b e são as distâncias origem-vértice, vértice-assíntota e origem-foco, respectivamente. Elementos de uma Hipérbole F1 e F2 → são os focos da hipérbole O → é o centro da hipérbole 2c → distância focal 2a → medida do eixo real ou transverso 2b → medida do eixo imaginário c/a → excentricidade Existe uma relação entre a b e c → c2 = a2 + b2·. Equação reduzida da hipérbole 1º caso: Hipérbole com focos sobre o eixo x.·. Fica claro que nesse caso os focos terão coordenadas F1 (-c , 0) e F2( c , 0). Assim, a equação reduzida da elipse com centro na origem do plano cartesiano e focos sobre o eixo x será: 2º caso: Hipérbole com focos sobre o eixo y. Neste caso, os focos terão coordenadas F1 (0 , -c) e F2(0 , c). Assim, a equação reduzida da elipse com centro na origem do plano cartesiano e focos sobre o eixo y será: Elementos da Elipse: F1 e F2 → são os focos C → Centro da elipse 2c → distância focal 2a → medida do eixo maior 2b → medida do eixo menor c/a → excentricidade Há uma relação entre os valores a, b e c→ a2 = b2+c2··. Equação da Elipse. 1º caso: Elipse com focos sobre o eixo x.·. Nesse caso, os focos têm coordenadas F1( - c , 0) e F2(c , 0). Logo, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo x será: 2º Caso: Elipse com focos sobre o eixo y. Nesse caso, os focos apresentam coordenadas F1(0 , -c) e F2(0 , c). Assim, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo y será: Elementos de uma parábola: Os elementos da parábola são figuras geométricas mais simples que ela e que fazem parte de sua definição e estão envolvidos em sua construção. São eles: Foco O ponto F da definição da parábola e da imagem anterior é chamado de foco e determina essa figura. Diretriz A reta r, também presente na definição e na imagem anterior, é chamada de diretriz da parábola. Essa reta é usada junto ao foco para a definição dessa figura. A distância entre qualquer ponto da parábola e a sua diretriz é igual à distância entre esse mesmo ponto da parábola e o seu foco. Parâmetro É a distância entre o foco e a diretriz. Esse cálculo pode ser feito por meio da distância entre ponto e reta. Vértice O vértice da parábola é o ponto mais próximo de sua diretriz. Existe uma propriedade que afirma o seguinte: VF = p2 Em que VF é o segmento da reta que tem início no vértice da parábola e tem fim em seu foco, e p é o parâmetro da parábola. Em outras palavras, o vértice de uma parábola fica no meio do caminho entre seu foco e a diretriz. Equações reduzidas da Parábola: a. Com o eixo de simetria coincidente com o eixo dos x e o vértice na origem. Seja P(x,y) e F(k,0) então y2 = 4kx b. Com o eixo de simetria coincidente com o eixo dos y e o vértice na origem Seja P(x,y) e F(0,k) então x2 = 4kx c. Com o eixo de simetria horizontal e vértice num ponto (m,n). Seja P(x,y) e F(m+k,n), então (y – n)2 = 4k(x – m) d. Com eixo de simetria vertical e vértice num ponto (m,n) Seja P(x, y) e F(m, n+k) então (x – m)2 = 4k (y – n) Aplicações da Elipse: A trajetória ao redor do Sol não é circular e sim elíptica (não considerando o deslocamento do sistema solar). Foi Kepler (1571-1630) quem desenvolveu esta teoria. No caso da Terra os semieixos são a = 153.493.000km e b = 153.454.000 km. Donde podemos obter a excentricidade da órbita da Terra: (quase uma circunferência) O eixo maior apresenta dois pontos: o periélio (janeiro) e o afélio (julho), que correspondem às distâncias mínimas e máxima da Terra ao Sol, respectivamente. Ademais, no globo terrestre (geoide) o equador tem aproximadamente a forma de uma circunferência e o meridiano de uma elipse. Arcos em forma de sei elipse são muito empregados na construção de pontes de concreto e de pedras (desde os antigos romanos) Engenharia Civil: em Resistência dos Materiais é muito empregada a elipse de inércia. Engenharia Elétrica: conjuntos de elipses homo focais (elipses de mesmo foco) são utilizadas na teoria de correntes elétricas estacionárias. Engenharia Mecânica: são usadas engrenagens elípticas (excêntricos). Sob uma abóboda elíptica os sons emitidos em um foco têm melhor audibilidade nos pontos próximos ao outro foco, não obstante serem praticamente inaudíveis na região intermediária aos dois focos. O mais portentoso monumento arquitetônico da Roma antiga foi o Coliseu. A planta baixa possuía a forma elíptica, cujo eixo maior tinha 188m e o menos 156m. Começou a ser construído em 72 por Vespasiano e foi concluído em 82 por Tito. A cobertura móvel, à altura de 85m, era sustentada por um sistema inédito de tirantes, adicionada em caso de chuva para proteger seus 40.000 espectadores. Diante da tribuna imperial, os garbosos gladiadores romanos desfilavam antes da luta e proferiam em alto e bom som: “Ave, César, morituri te salutant” (Salve César, os que vão morrer te saúdam). Exemplo: Uma aplicação óptica pode ser encontrada no dispositivo de iluminação dos dentistas. Este consiste num espelho com a forma de um arco de elipse e numa lâmpada que se coloca no foco mais próximo. A luz da lâmpada é concentrada através do espelho no outro foco, que é ajustado pelo dentista para estar num ponto dentro da boca de seu paciente. Aplicações da parábola A parábola apresenta várias aplicações, alguns exemplos são as antenas parabólicas, faróis de veículos, fornos solares e em telescópios. Em particular, no caso dos fornos ou coletores solares os raios de luz ao encontrarem um espelho parabólico convergem para o foco do espelho, onde a temperatura pode chegar a 3.500°C e neste ponto é colocado um dispositivo que irá utilizar a energia concentrada. Essa energia pode ser usada para gerar eletricidade, derretimento de aço, fazer combustível de hidrogênio ou nano materiais. Referências Bibliográficas: http://www.dmm.im.ufrj.br/projeto/rived/modulo_excentricidade/excen_teoria.html, acesso em 30/09/2018. https://pt.wikibooks.org/wiki/C%C3%A1lculo_(Volume_2)/C%C3%B4nicas, acesso em 30/09/2018. http://www.mat.uc.pt/~adsg/AM4conicas.pdf, acesso em 29/09/2018 PAIVA, Manoel. Matemática , volume 3. 2ª edição, Moderna. São Paulo, 2013.








![Questão 1 [2,0 pontos] A partir da definição de parábola, obtenha](http://s1.studylibpt.com/store/data/006213354_1-22d389aa1b10b9d278ad3eef2bc9aef4-300x300.png)