referências bibliográficas

FICHA PARA IDENTIFICAÇÃO
PRODUÇÃO DIDÁTICO – PEDAGÓGICA
TURMA - PDE/2012
Título:
CONSULTA AO SOFTWARE GEOGEBRA NA
CONSTRUÇÃO DE TRIANGULOS NOTÁVEIS
Autor
MARIA DEOLINDA SCREMIN
Disciplina/Área (ingresso no PDE)
MATEMÁTICA
Escola de Implementação
Projeto e sua localização
COLÉGIO ESTADUAL ELEODORO ÉBANO PEREIRA
do
Município da escola
CASCAVEL
Núcleo Regional de Educação
CASCAVEL
Professor Orientador
SÉRGIO FLÁVIO SCHMITZ
Instituição de Ensino Superior
UNIOESTE
Relação Interdisciplinar
ARTES
(indicar, caso haja, as diferentes
disciplinas compreendidas no
trabalho)
Resumo
(descrever a justificativa, objetivos
e
metodologia
utilizada.
A
informação deverá conter no
máximo 1300 caracteres, ou 200
palavras, fonte Arial ou Times
New Roman,
tamanho 12 e
espaçamento simples)
JUSTIFICATIVA DO TEMA DE ESTUDO
O ensino e a aprendizagem da matemática é algo que ainda
hoje é desafiante para educadores e escola. Quando se trata
do ensino da geometria para alunos de 8º ano do Ensino
Fundamental, ampliam-se as dificuldades pela exigência de
interpretação,
raciocínio
lógico,
cálculos algébricos,
representação, classificação, identificação de regularidades e
o conhecimento das relações quantitativas e qualitativas que
esta linguagem matemática necessita.
Percebe-se que quando este ensino se restringe a resolução
de atividades com recursos limitados como o livro didático, o
quadro de giz, o caderno, o compasso e a régua por exemplo,
a aprendizagem nem sempre acontece com todas as suas
possibilidades, pois se baseia apenas em um professor que
ensina e um aluno que recebe o conhecimento, ou não, como
em muitos casos acontecem.
Por outro lado, vive-se um momento de intensas
transformações que aceleram o processo de aquisição de
informações e de conhecimento por meio da utilização da
informática e de recursos tecnológicos de comunicação, os
quais o público jovem tem acesso e um domínio técnico,
muitas vezes, maior que outros públicos, inclusive os
professores.
Diante disso, este projeto de intervenção se justifica por aliar
conhecimentos de informática e aprendizagem da Geometria
Plana. Por meio da utilização do software Geogebra, alunos
de 8º ano do Colégio Estadual Eleodoro Ébano Pereira, terão
meios de ampliar os conhecimentos obtidos em sala de aula,
com uma ferramenta de aprendizagem interativa. Assim, estes
estudantes terão a oportunidade de descobrir, por meio de
uma nova ferramenta, meios para visualizar, explorar,
socializar e fazer conjecturas, ampliando com isso seus
conhecimentos geométricos.
OBJETIVOS
OBJETIVO GERAL: Possibilitar a aprendizagem da Geometria
Plana por meio da utilização do software Geogebra por alunos
do 8º ano do Ensino Fundamental.
OBJETIVOS ESPECÍFICOS:
como ferramentas pedagógicas para o ensino da Geometria.
tais como o raciocínio lógico, a interpretação, a dedução, a
criatividade e a autonomia.
ensino dos conteúdos de Geometria Plana.
das diversas formas geométricas.
METODOLOGIA
A primeira parte do trabalho se configura no estudo teórico e
prático da aplicação do software geogebra, por parte do
professor PDE.
Serão elaborados exercícios que possam ser utilizados pelos
alunos com o uso do aplicativo. Estes exercícios partirão da
contextualização de atividades de geometria plana para a
resolução de problemas do cotidiano, de modo que eles
percebam a aplicabilidade da geometria na vida em
sociedade.
Na primeira quinzena do mês de maio, o projeto será
apresentado ao diretor da escola, à equipe pedagógica e aos
professores de matemática das turmas selecionadas para o
projeto de intervenção.
O projeto também será apresentado aos educandos. Por meio
de entrevistas com os educandos e algumas atividades feitas
em sala de aula com materiais convencionais (lápis, régua,
compasso, caderno, etc.), para a resolução de algumas
atividades diagnosticaremos o nível de conhecimento que os
mesmos possuem sobre Geometria Plana.
O trabalho com os alunos será dividido em quatros oficinas:
principais conceitos da Geometria Plana e a resolução de
algumas atividades pelo método convencional.
Geogebra tendo acesso aos principais comandos e recursos
do mesmo.
alunos resolvam utilizando os recursos do Geogebra.
, propõe-se que os alunos em grupo criem
atividades (situações-problema) de Geometria que possam
ser resolvidas com a utilização do Geogebra.
O último encontro no mês de julho será reservado a avaliação
por parte dos alunos, da equipe pedagógica, dos professores
e da direção da escola.
Palavras-chave ( 3 a 5 palavras)
TRIÂNGULOS – GEOGEBRA - GEOMETRIA
Formato do Material Didático
Livro Temático On-line
TRIÂNGULOS NOTÁVEIS
Público Alvo
(indicar o grupo para o qual o
material didático foi desenvolvido:
professores, alunos,
comunidade...)
Alunos
CONSULTA AO SOFTWARE GEOGEBRA NA
CONSTRUÇÃO DE TRIANGULOS NOTÁVEIS
TRIÂNGULOS
O USO DO GEOGEBRA COMO FERRAMENTA PARA CONSTRUÇÃO,A
INTERPRETAÇÃO E A APRENDIZAGEM DA GEOMETRIA PLANA
Este material é apresentado através de textos explicativos e informativos
quanto a utilização e construção dos triângulos notáveis com a utilização do
software Geogebra e uma breve história da aplicabilidade do triângulo no
decorrer da vida humana.
O livro produzido, tem como objetivo abordar o assunto,procurando enfocar
os triângulos notáveis, para que os alunos possam ter como consulta, através
de http://issuu.com/mdscremin/docs/livro_digital_final_14_08,sempre
que encontrarem dúvidas nas suas atividades.
Vejo a necessidade de trabalhar a construção das figuras planas, uma vez
que, o ensino e a aprendizagem da geometria, é algo que ainda hoje é
desafiante para educadores e escola. Quando se trata do ensino da geometria
para alunos de 8º ano do Ensino Fundamental, ampliam-se as dificuldades pela
exigência
de
interpretação,
raciocínio
lógico,
cálculos
algébricos,
representação, classificação, identificação de regularidades e o conhecimento
das relações quantitativas e qualitativas que esta linguagem matemática
necessita.
Vive-se um momento de intensas transformações que aceleram o
processo de aquisição de informações e de conhecimento por meio da
utilização da informática e de recursos tecnológicos de comunicação, os quais
o público jovem tem acesso e um domínio técnico, muitas vezes, maior que
outros públicos, inclusive os professores.
Diante disso, este livro on-line se justifica por aliar conhecimentos de
informática e aprendizagem da Geometria Plana. Através da utilização do
software Geogebra, alunos de 8º ano do Colégio Estadual Eleodoro Ébano
Pereira, terão meios de ampliar os conhecimentos obtidos em sala de aula,
com uma ferramenta de aprendizagem interativa. Assim, estes estudantes
terão a oportunidade de descobrir, por meio de uma nova ferramenta, meios
para visualizar, explorar, socializar e fazer conjecturas, ampliando com isso
seus conhecimentos geométricos.
HISTÓRIA DA UTILIDADE DO TRIÂNGULO
Pode ser que ao longo de sua evolução, o homem sentiu necessidade de
tornar as construções rígidas e mais seguras. Por exemplo nos tempos
primitivos da civilização Grega, foi usado pelos gregos o triângulo de descarga,
onde permite descarregar as pressões exercidas por grandes pesos que se
encontram por cima das portas.
Fig.01 http://www.prof2000.pt/users/secjeste/modtri01/Imagens/Image01.jpg
Geralmente esses triângulos eram abertos, mas temos exemplos como na
cidade de Mecenas, onde a porta dos leões é decorada.
Fig.02 http://www.prof2000.pt/users/secjeste/modtri01/Imagens/porta600.jpg
No princípio da idade Média, apareceu pela primeira vez no mediterrâneo, uma
vela triangular, porém não se sabe quem a usou primeiro.
Fig.03 http://www.prof2000.pt/users/secjeste/modtri01/Pg000700.htm
VELA TRIÂNGULAR
Os Portugueses mantiveram durante muitos anos, o segredo desta arte
no Oceano. Por isso chegaram até ao Cabo da Boa Esperança, sem a
concorrência do resto da Europa. Em 1575, o escritor Escalante de Mendonça
escrevia:..."A Caravela Portuguesa foi a melhor invenção que até ao tempo se
alcançou para a navegação de bolina." Mas os triângulos continuam sendo
utilizados, veja exemplos:
FIGURA 04 http://www.prof2000.pt/users/secjeste/modtri01/Pg000710.htm
FIGURA 04 http://www.prof2000.pt/users/secjeste/modtri01/Pg000710.htm
FIGURA 05 http://www.prof2000.pt/users/secjeste/modtri01/Pg000730.htm
TUTORIAL (PASSO A PASSO)
ESTRATÉGIAS DE AÇÃO
Instalação do programa no Microsoft Windows
Proceda da seguinte forma:
1.Acesse a página oficial do programa: WWW.geogebra.org;
2.Clique na opção Download que fica na coluna esquerda da tela.
3.Clique em: Download Geogebra.
4.Aparecerá em parte da tela, a figura 1 deste texto, onde deverá selecionar a
opção de acordo com o seu sistema operacional.
5.Ao aparecer a próxima tela, clique em salvar.
6.Crie uma pasta para o GEOGEBRA, clicando em “nova pasta”.
7.Dê dois cliques na nova pasta para selecioná-la, em seguida cliqu SALVAR.
8.Aguarde e ao concluir o donwload, clique em FECHAR.
9.Finalmente aparecerá a tela do GEOGEBRA para iniciar o trabalho.
Observação: Caso não consiga executar o programa, será necessário baixar a
máquina virtual Java, a partir do site http://www.getjava.
Após baixado o arquivo de instalação.
Após instalar o programa GEOGEBRA,estude o software, verifique o que fazer
com os botões básicos para que possa descobrir o que é possível fazer.
Abaixo, pode verificar seguindo o passo a passo.
Na parte superior à esquerda está a parte algébrica, que pode ser fechada se
necessário, e à direita a parte geométrica. Para reativar a parte algébrica basta
ir ao item exibir do menu e clicar em "janela de álgebra". Neste mesmo item
podemos ativar/desativar os eixos, a malha e o protocolo de construção. Na
tela abaixo temos cada ícone com várias opções de acordo com o desenho.
Por exemplo
ao clicar na parte inferior a direita do ícone conhecemos
seus nomes e utilidades.
O conhecimento e exploração das ferramentas é fundamental para execução
das atividades.
Na sequência explore todos os ícones da barra de ferramentas e exercite
atividades simples como, apagar, alterar, limpar tela, construir figuras planas,
para que brincando possa conhecer e executar atividades.
Construa vários triângulos com o botão segmento de reta definido por dois
pontos, em seguida,use também ponto médio, perpendicular,bissetriz e se
desafie a construir triângulos retângulo, eqüilátero, e isósceles como também
em mover, fazer, desfazer e medir os ângulos dos triângulos, no intuito de usar
o dinamismo do programa,como também experimentando a propriedade da
soma dos ângulos internos de qualquer dos triângulos que sempre é 1800.
Observação: Precisamos lembrar que o sistema decimal aparece ponto no
lugar da vírgula.
Espécies de triângulos: eqüilátero, escaleno, isósceles e retângulo.
a)Triângulo eqüilátero. Tem os três lados e três ângulos iguais.
b)Triângulo retângulo. Possui um ângulo reto.
Triângulo escaleno. Tem todos os ângulos e lados desiguais.
Triângulo isósceles.Tem dois lados e, portanto, dois ângulos iguais.
PONTOS NOTÁVEIS DE UM TRIÂNGULO
Será estudado os pontos notáveis de um triângulo:Baricentro, Incentro,
Circuncentro e Ortocentro, construindo os triângulos, retângulo, isósceles,
escaleno e eqüilátero, através do Software Geogebra.
Através das Ceviana Mediana,Bissetriz interna e altura. O nome
Ceviana, foi dado em homenagem ao matemático italiano Giovani Ceva(16481734), que demonstrou teoremas importantes sobre elas. Ceviana é todo
segmento que tem uma das extremidades num vértice qualquer de um
triângulo e a outra num ponto qualquer da reta oposta a esse vértice.
a) Mediana é toda Ceviana que une um vértice ao ponto médio do lado oposto.
b) Bissetriz Interna é um segmento de reta ou ceviana que divide o ângulo
interno .em dois ângulos congruentes.
c) Altura é uma perpendicular que une o vértice ao seu lado oposto.
d) Mediatrizes são retas perpendiculares, passando pelo ponto médio, a cada
um dos lados de um triângulo.
A) BARICENTRO As três medianas de um Triângulo interceptam-se num
mesmo ponto que divide cada mediana em duas partes, sendo que a
parte que contém o vértice é o dobro da outra.
Uma estrada muito inclinada, poderá causar o tombamento de um veículo cujo
o centro de gravidade seja muito alto, como um jipe ou um caminhão.
Propriedade: O ponto de encontro das três medianas de um triângulo qualquer
é o centro de massa desse triângulo, denominado Baricentro, denotado por(G).
b) INCENTRO
O ponto de intersecção das três bissetrizes é denominado INCENTRO,
denotado por (I) e se encontra a igual distância dos lados do triângulo. O
INCENTRO é o centro da circunferência inscrita num triângulo.
c) CIRCUNCENTRO é o ponto de encontro das mediatrizes dos lados do
triângulo, denotado por ( O ). É também o centro da circunferência circunscrita
a um triângulo.
O Circuncentro pode ser:
Interno: se o triângulo for acutângulo.
Externo: se o triângulo for obtusângulo
Coincidente: se o triângulo for retângulo
d) ORTOCENTRO
O ponto de intersecção das alturas de um triângulo é chamado de Ortocentro e
denotado por ( H ).
O Ortocentro pode ser:
Interno: se o triângulo for acutângulo.
Externo: se o triângulo for obtusângulo
Coincidente: se o triângulo for retângulo.
Procure realizar as atividades na ordem proposta, no passo a passo, pois as
definições e ferramentas estão sendo exploradas gradativamente.
Passo a passo: clicar em
assim um triângulo.
polígonos e ligar os pontos ABC, formando
Clicar em
e nos vértices ABC,BCD e CAB que automaticamente surge a
medida de cada ângulo.
CONDIÇÃO DE EXISTENCIA DE UM TRIÂNGULO
-Desenhar triângulos com medidas quaisquer
Passo a passo
Clicar no programa Geogebra, e no ícone
segmento definido por dois
pontos. Ligar os pontos AB, BC,CD com medidas quaisquer. Clicar em ângulos
e somar os ângulos . Â +B +Ĉ = 180 0 Construir vários triângulos e aplicar a
propriedade.
Outro modo de construir triângulos
Clicar em ângulos e ligar os pontos formando triângulos
1-CONSTRUÇÃO DO BARICENTRO Após construir o triângulo clique
em
na tecla ponto médio
, e nos pontos AB, BC e CA formando
os pontos médios, em seguida una
seguimento definido por dois pontos
unindo o ponto médio a seus respectivos vértices.
2. ORTOCENTRO: Construa um triângulo qualquer, clicando em polígonos e clique na
tela
janela
três alturas.
unindo os três vértices, em seguida determine as suas três alturas através da 4a
reta perpendicular e clicar em cada vértice ao seu lado oposto, onde formará as
Para medir o ângulo dos triângulos Clicar
ângulo. Veremos que cada altura medirá 900.
nos três ângulos teremos a medida de cada
3-CIRCUNCENTRO
Construa um triângulo equilátero, seguindo os passos abaixo.
.Clicar em segmento de reta
.construir uma reta de tamanho qualquer.
Clicar em círculo dados centro e um de seus pontos
extremidade da reta
Abrir até a
.Repetir, abrindo o circulo até a outra extremidade.
.Clicar em
formando o ponto C. É só unir os três pontos com polígonos e
está concluído o triângulo eqüilátero.
Para eliminar, clicar com o mause, botão direito, em cima da circunferência,
aparece o ícone exibir objeto, clicar e apaga.Ficando apenas o triângulo
equilátero.
Para determinar as mediatrizes clicar no ícone
que surgem com a união das três
mediatriz, em cada reta
o ponto de intercecção.
Em seguida clicar
círculo dados centro e um de seus pontos,em cima do
ponto de união das três mediatrizes, a circunferência se abre até o vértice.
Surgindo assim a circunferência circunscrita.
4-INCENTRO
Construa um triângulo qualquer
Clicar em
e em A^BC , BCA e CAB, onde forma as bissetrizes.
5-CIRCUNFERÊNCIA INSCRITA
-Construa um triângulo e encontre suas bissetrizes
-Clique em
e com o rato no ponto de intersecção das bissetrizes (incentro) abrindo o
circulo até atingir o lado dos triângulos.
Proponho que a partir dos conhecimentos adquiridos construam:
triângulos isósceles
triângulos eqüiláteros
triângulos escaleno
triângulos retângulos
determinem o baricentro, ortocentro, incentro e circuncentro de cada um,
observando e registrando as conjecturas em cada caso.
TEOREMA DE PITÁGORAS
O teorema de Pitágoras leva o nome do matemático grego Pitágoras (570 a.C.
– 495 a.C.), que tradicionalmente é creditado pela sua descoberta
e demonstração.
Pitágoras descobriu que em qualquer triângulo retângulo, o quadrado do
comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos
dos catetos. Traduzindo para uma equação, temos: H2 = C2 + C2
Por definição, a hipotenusa é o lado oposto ao ângulo reto, e os catetos são os
dois lados que o formam. O enunciado anterior relaciona comprimentos, mas o
teorema também pode ser enunciado como uma relação entre áreas:
Em qualquer triângulo retângulo, a área do quadrado cujo lado é a
hipotenusa, é igual à soma das áreas dos quadrados cujos lados são os
catetos, assim temos a equação: c2 = a2 + b2
ou seja : H2 = C2 + C2
O teorema de Pitágoras: a soma das áreas dos quadrados
construídos sobre os catetos (a e b) equivale à área do
quadrado construído sobre a hipotenusa (c).
Podemos fazer a verificação
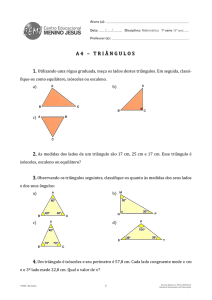
Observe os triângulos abaixo:
CURIOSIDADES
Por que Triângulo das Bermudas ?
ILHA DAS BERMUDAS
:
FLÓRIDA
PORTO RICO
Ufa!!!chamado
Mar do diabo””
Cemitério de barcos””...
barcos e aviões
sumiram e não
deixaram
vestígios.
Somem sem deixar
Vestígios!!!
Alguns foram
encontrados, porém sem
nenhuma pessoa a bordo
Existem no planeta vários outros pontos conhecidos como portais do diabo ou
triângulos de tempestades magnéticas, mas o mais famoso, sem dúvida é o Triângulo
das Bermudas.
REFERÊNCIAS BIBLIOGRÁFICAS
GERÔNIMO,João
Roberto;
OLIVEIRA
BARROS,Rui
marco
e
FRANCO,Valdeni soliani.Geometria Euclidiana plana-Um estudo com o
Software Geogebra.
NÓBREGA, J. cássio. Aprendendo MATEMÁTICA COM O GEOGEBRA.
www.prof2000.pt/users/secjeste/modtri01/Pg000700.ht
m
Desejo que este tutorial, seja útil, como apoio, em suas
consultas.
É
só
acessar
http://issuu.com/mdscremin/docs/livro_digital_final_14_08.
Professora: Maria Deolinda Scremin
CASCAVEL, PDE 2012
QUE TENHA ÓTIMO APROVEITAMENTO