Domínio 5: Funções

Ficha de revisão 5
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
/20
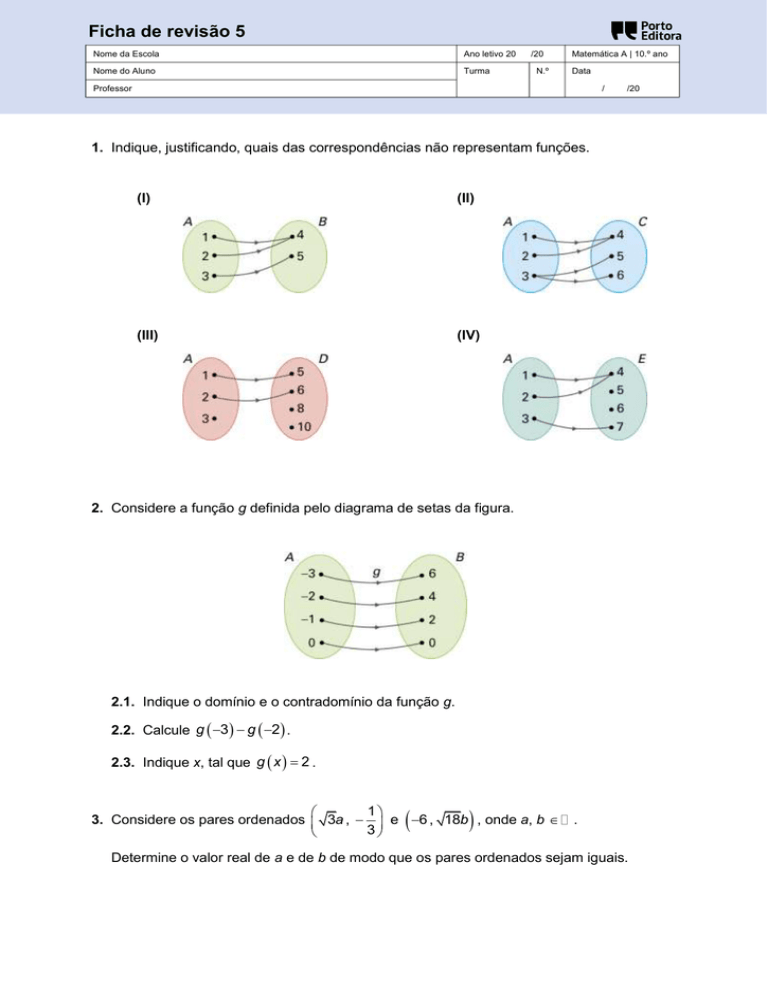
1. Indique, justificando, quais das correspondências não representam funções.
(I)
(II)
(III)
(IV)
2. Considere a função g definida pelo diagrama de setas da figura.
2.1. Indique o domínio e o contradomínio da função g.
2.2. Calcule g  3   g  2 .
2.3. Indique x, tal que g  x   2 .


1

3. Considere os pares ordenados  3a ,   e 6 , 18b , onde a, b 
3

.
Determine o valor real de a e de b de modo que os pares ordenados sejam iguais.
Ficha de revisão 5
4. Considere a função de A em B, sendo A  2 ,  1,1, 3 e B  1, 4 , 9 .
O gráfico da função f é Gf   2 , 4 ,  1,1 , 1,1 , 3 , 9  .
4.1. Represente a função f por um diagrama de setas.
4.2. Represente a função f por um gráfico cartesiano.
5. Considere a função h tal que:
h: AB
x1
 2x 
1
2
5 
 3
sendo A   ,  1, , 3 .
2 
 2
5.1. Determine o contradomínio da função h.
5.2. Represente a função h por um gráfico.
6. Considere, definidas em
●
f x 
x
3
, as funções afins f , g, h e j, tais que:
●
g x 
x
3
2
●
hx  2
●
j  x   2x
6.1. Identifique as funções constantes e as funções lineares.
6.2. Admita que os gráficos cartesianos das funções g e j estão representados no mesmo
referencial cartesiano. Determine o valor de x tal que g  x   j  x  e interprete
geometricamente o valor obtido.
7. Indique, justificando, o valor lógico de cada uma das proposições.
7.1. p : A função f definida por f  x   3x é uma função de proporcionalidade direta.
7.2. q : Numa função, objetos diferentes podem corresponder à mesma imagem.
7.3. r : A função g definida por g  x  
constante de proporcionalidade é
7.4. t : x 

2
é uma função de proporcionalidade inversa cuja
x
1
.
2
: f  x   2 , sendo f  x   3 x .
Miniteste 1 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
1. Considere os conjuntos A  1, 2 e B 
1.1. O par ordenado


/20

2, 3, 5 .

2 ,1 pertence a A  B ? Justifique.
1.2. Represente em extensão A  B .
1.3. Indique um elemento de A2  B3 e determine o cardinal de A2  B3 .
2. Considere as funções reais de variável real f e g, definidas por f  x  
x 1
e g x 
x  x2
x2
.
x
Caracterize cada uma das funções.
Questão-aula 1
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Professor
Na figura está representada, num referencial ortonormado, parte do gráfico
de uma função g definida em

. Em qual das figuras seguintes poderá
1
estar parte da representação gráfica da função g ?
(A)
(B)
(C)
(D)
Item de construção
2.
Data
/
Item de seleção
1.
Matemática A | 10.º ano
Considere as funções reais de variável real, f e g, definidas por:
f x  x  3
e g x 
1
x  3
2
2.1.
Determine o domínio de cada uma das funções f e g.
2.2.
Mostre que a função f é injetiva.
2.3.
Calcule  g f 
 3.
Apresente o valor pedido com denominador racional.
/20
Miniteste 2 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
1. Considere a função definida, em
/20
, por f  x   x 3  2x e o respetivo gráfico representado
num plano munido de um referencial cartesiano.
1.1. Mostre que f é uma função ímpar.
1.2. Mostre que os pontos do gráfico de f de abcissas respetivamente iguais a
2 ea  2
são simétricos relativamente à origem do referencial.
1.3. Seja a  Df e P a , f a   um ponto do gráfico de f .
1.3.1. Indique as coordenadas do ponto Q do gráfico de f de abcissa –a.
1.3.2. Prove que o ponto médio do segmento de reta [PQ] é o ponto O, origem do
referencial.
1.3.3. Admita que b 
a
.
2
Determine o valor de f  a   f  2b  .
2. Considere uma função g definida em Dg 
.
Na figura está representado, num plano munido de um referencial cartesiano, parte do gráfico
da função g.
Complete o gráfico sabendo que g é uma função par.
Questão-aula 2
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
/20
Item de seleção
1.
Seja f uma função real de variável real, tal que:


● f é uma função injetiva;
● f  2  5;
● f 1 é a função inversa de f;
● f é uma função ímpar.
O valor de f 1  5  é:
(A)
(B)
2
 2
(C)
2
5
(D)
5 2
Item de construção
2.
Na figura está representado, num plano munido de um referencial cartesiano, o gráfico da
função f definida em  3 , 4  onde foram assinalados os pontos A e B pertencentes ao
gráfico de f.
2.1.
Indique o contradomínio da função f.
2.2.
Defina analiticamente o segmento de reta [AB].
2.3.
A função f tem exatamente dois zeros, um negativo e outro positivo.
Indique o zero positivo e determine o zero negativo.
2.4.
Considere a função g tal que, para todo o x  Dg , g  x   f  x  2   1 .
2.4.1.
Explique como pode obter o gráfico da função g a partir do gráfico da função f.
2.4.2.
Seja Dg   a , b  1 o contradomínio da função g.
Determine o valor real de a e de b.
2.5.
Considere a função h, tal que, para todo o x  Dh , h  x   f  x   2b .
Indique os valores reais de b de modo que a função h não tenha zeros.
Miniteste 3 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
/20
1. Na figura está representado, num referencial ortonormado,
o gráfico da função f.
1.1. Indique o domínio e o contradomínio da função f.
1.2. Determine, analiticamente, o zero da função f.
1.3. Indique um intervalo onde a função f seja injetiva.
1.4. Construa uma tabela de variação para a função f.
1.5. Estude a função f quanto à monotonia.
1.6. Indique, se existirem, os extremos absolutos, os extremos relativos, os maximizantes e
os minimizantes da função g.
Questão-aula 3
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
/20
Item de seleção
1.
Relativamente a uma função real de variável real f, sabe-se que f  a  não é o mínimo, nem
relativo nem absoluto.
Qual dos gráficos seguintes poderá ser o da função f?
(A)
(B)
(C)
(D)
Itens de construção
2.
Considere a função real de variável real, definida em
, por f  x   3  6 x .
Prove, recorrendo a processos exclusivamente analíticos, que a função f é decrescente.
3.
Esboce o gráfico de uma função f tal que:
●
tenha domínio
;
●
seja estritamente crescente em
●
o contradomínio seja 1, 3 ;
.
Miniteste 4 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
Matemática A | 10.º ano
N.º
Data
Professor
/
1. Considere a função f, de domínio
/20
, definida por f  x   2x 2  8x  10 .
1.1. Escreva f  x  na forma a  x  h   k , onde a 
2
\ 0 e h , k 
.
1.2. Indique:
● as coordenadas do vértice da parábola que define o gráfico da função f;
● uma equação do eixo de simetria do gráfico da função f;
● o contradomínio da função f.
1.3. Resolva, em
, a condição f  x   10 .
Apresente o conjunto-solução usando a notação de intervalos de números reais.
1.4. Relativamente ao gráfico de f sabe-se que A e B são os pontos onde o gráfico interseta
o eixo das abcissas (a abcissa de A é menor que a abcissa de B) e C é o ponto de
interseção do gráfico com o eixo das ordenadas.
Determine a área do triângulo [ABC].
1
. Considere, ainda, a
2
função h, também de domínio , definida por h  x   g  x  a   b . Determine o valor real de
a e de b de modo que o gráfico da função h e tenha o vértice na origem do referencial quando
representado num plano munido de um referencial cartesiano.
2. Considere a função g, de domínio
, definida por g  x    x 2  3 x 
Questão-aula 4
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
Item de seleção
1. Seja f uma função quadrática, definida em
Seja g a função definida em
(A)
 6 ,   
(B)
, e cujo contradomínio é  , 4  .
por g  x   f  x   2 . Qual é o contradomínio da função g?
 6 ,  
(C)
 2 ,   
(D)
2 ,  
Item de construção
2. Para cada valor de c a expressão f  x   2x 2  3x  c define uma função f.
2.1. Determine para que valores reais de c:
2.1.1. a equação f  x   0 é impossível em ;
2.1.2.
2.2.
/20
o gráfico de f passa no ponto de coordenadas


2 , 1 .
Indique, justificando, o valor lógico de cada uma das proposições.
3
3
3
2.2.1. f  5  f  
2.2.2. Se x  , então f  x   f   .
4
4
 
4
1
2.2.3. Se c  , o contradomínio de f é  , 1 .
4
Miniteste 5 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
Matemática A | 10.º ano
N.º
Data
Professor
/
/20
, sabe-se que Df   , 2 .
1. De uma função quadrática f, de domínio
1.1. Indique o contradomínio de cada uma das funções.
1.1.1. g  x   f  x   3
1.1.2. h  x   f  x   1
1.2. Determine os valores reais para os quais a função j, definida por j  x   f  x   a , não
tem zeros.
2. Considere a função f, definida em
2
, por f  x   x  4 x  3 .
2.1. Determine os valores de x para os quais f  x   f


3 2 .
2.2. Determine os intervalos em que f é positiva e os intervalos em que f é não positiva.
Questão-aula 5
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
Matemática A | 10.º ano
N.º
Data
Professor
/
Item de seleção
1.
, definida por g  x   2x 2  4 x  1 .
Considere a função g, de domínio
Qual é o contradomínio da função g?
(A)
 ,  3
(B)
 1,  
(C)
 3 ,  
 ,  1
(D)
Item de construção
2.
Considere a função f, de domínio
, definida por f  x   6x 2  24x  25 .
2.1.
Mostre que f  2  x   f  2  x  , x 
2.2.
Escreva f  x  na forma a  x  h   k , onde a 
2.3.
Estude a função f quanto ao sinal.
2
\ 0 e h, k 
.
/20
Miniteste 6 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
1. Considere a função h definida em
3  x
por h  x    2
x  1
/20
se x  2
se x  2
1.1. Esboce o gráfico da função h.
1.2. Calcule o valor exato de h  2  h
 2   h 2 2  .
1.3. Resolva, em  , 2 , a condição h  x   8 .
Apresente o conjunto-solução usando a notação de intervalos de números reais.
2. Represente sob a forma de intervalos ou uniões de intervalos os conjuntos-solução das
condições seguintes:
2.2. 3 x  4  2
2.1. 1  x  3  2
2.3. 10 x  2x 2  12
Questão-aula 6
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
Professor
/20
N.º
Matemática A | 10.º ano
Data
/
/20
Item de seleção
1.
Considere uma função f de domínio
domínio
e contradomínio   2 , 3 3  . Seja h a função de


definida por h  x   f  x   3 . Qual é o contradomínio da função h?
(A) 0 , 2  3 


(B) 0 , 2 3 


(C) 0 , 2  4 3 


(D) 0 , 4 3 


Item de construção
2.
Considere a função g definida em
2.1.
2.2.
por g  x   12  2 4  2x .
Defina, analiticamente, a função g, sem utilizar módulos.
Represente sob a forma de intervalos ou uniões de intervalos os conjuntos-solução das
seguintes condições em :
2.2.1. g  x   8
2.3.
2.4.
2.2.2. g  x   2
Determine, analiticamente, os zeros da função g.
Indique o contradomínio da função g.
Miniteste 7 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
1. Sejam f e g duas funções definidas em
1.1. Seja h a função de domínio
/20
por f  x   4  2x  3 e g  x   3x  1  3 .
x
definida por h  x   f   .
2
 1
Determine h  4   h   .
2
1.2. Resolva, em
, a condição f  x   g  x  .
2. Represente sob a forma de intervalos ou uniões de intervalos os conjunto-solução das
seguintes condições em
.
2.1. 4  x 2  3 x
2.2. x 2 
3
x 1
2
Questão-aula 7
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Professor
Matemática A | 10.º ano
Data
/
Item de seleção
1.
Na figura está representada, num plano munido de um referencial
ortonormado, parte do gráfico da fnção f de domínio
Considere, ainda, a função h, definida em
.
por h  x   f  x  .
Qual das seguintes equações tem exatamente três soluções?
(A) f  x   3
(B) f  x   0
(D) f  x   1
(C) f  x   2
Item de construção
2.
Na figura está representada, num plano munido de um referencial
ortonormado, parte do gráfico de uma função f de domínio
Considere, ainda, a função g, definida em
.
por g  x   f  x   3 .
2.1.
Mostre que a função f pode ser definida por f  x   x 2  6x  8 .
2.2.
Resolva a condição g  x   0 .
2.3.
2
Mostre que g  2   g 3  2    f 1  4  .




2
/20
Miniteste 8 (20 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
/20
1. Considere as funções f e g definidas, respetivamente, por f  x   2  x  3 em  3 ,   e
g  x   x 2  3 x em
.
1.1. Esboce o gráfico das funções f e g.
1.2. Determine os zeros de f.
1.3. Utilizando a calculadora gráfica, determine valores aproximados às décimas das
soluções da equação f  x   g  x  .
2. Resolva as seguintes equações, simplificando tanto quanto possível as expressões que
representam as respetivas soluções.
2.1.
8x  12  x  3
2.2.
3x  6  x  2
2.3.
3
3  4x  3
Questão-aula 8
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Professor
Matemática A | 10.º ano
Data
/
/20
Item de seleção
1.
Considere a função real de variável real g, definida em  3 ,    por g  x    3  x  3 .


Qual é o contradomínio da função g?
(A)   ,

3 
(B)  3 ,   


(C)   ,  3 


(D)  3 ,   


Item de construção
2.
Considere as funções f e g definidas por f  x   1  2 x e g  x   x  1.
2.1.
2.2.
2.3.
Determine o domínio de cada uma das funções f e g.
Determine o domínio da função h  f  g e determine os zeros de h.
f 1
f 
Determine   12 
. Apresente o resultado com denominador racional.
g 3
g
Ficha de preparação para o teste de avaliação 5
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
/20
N.º
Matemática A | 10.º ano
Data
Professor
/
definida por h  x  
1. Considere a função h de domínio
/20
1
x  b , sendo b é uma constante
2
real.
1.1. Justifique que a função h é bijetiva.
1.2. Caracterize a função h 1 , inversa da função h.
2. Na figura está representada, num referencial ortonormado, parte do gráfico de uma função f.
Seja f 1 a função inversa de f.
2.1. Calcule o valor exato de
f 1  2 
3  f 1   3 
.
Apresente o valor pedido com denominador racional.
2.2. Esboce o gráfico da função f 1 .
3. Na figura está representada num plano munido de um referencial cartesiano a função g
definida em .
3.1. Esboce o gráfico da função h definida por h  x   g  x  2  1 .
3.2. Considere a função f tal que, para todo o x  Df , f  x   g  x  a   b .
Indique os valores reais de a e de b, tais que:
3.2.1. a função f tenha exatamente um zero;
3.2.2. o contradomínio da função f seja, Df    ,

3.2.3. a função f seja par.
3  ;
Ficha de preparação para o teste de avaliação 5
4. O gráfico de uma função afim f interseta o eixo Ox em x  3 e o eixo Oy no ponto de
ordenada –4.
4.1. Determine:
4.1.1. a forma canónica de f;
4.1.2. os zeros da função g definida por g  x   f  x  2 ;
4.1.3. a ordenada do ponto de interseção do eixo Oy com o gráfico da função h definida
por h  x   f   x   3 .
4.2. Esboce o gráfico da função j definida por j  x   2f   x   4 .
5. Relativamente a uma função f, de domínio
●
f 0  2
●
f é estritamente crescente em 0 ,   ;
●
f é par.
, sabe-se que:
5.1. Faça um esboço de uma função f compatível com as informações dadas.
5.2. Relativamente à função f, qual das seguintes afirmações é verdadeira?
(A) O contradomínio de f é 0 ,   .
(B) f é estritamente crescente em
(C) f é injetiva.
(D) f não tem zeros.
.
6. Considere uma função h definida em  5 ,   , tal que a sua tabela de variação é:
x
–5
–1
5
2
2 2

hx
2
2
0
4

6.1. Esboce o gráfico de uma função h que seja compatível com as informações contidas na
tabela.
6.2. Indique o conjunto-solução de cada uma das condições.
6.2.1. h  x   4
6.2.2. h  x   0
7. Represente sob a forma de intervalos ou uniões de intervalos os conjuntos-solução das
seguintes condições em :
7.1. 2x 2  6x
7.2. x 2  4  3 x
7.3. x  x  2  2  6  x 
7.4.
7.5. x  2  1  2 x
7.6.  x 2  x  2  4
 x  2
2
 2
Ficha de preparação para o teste de avaliação 5
8. Considere a função g tal que:
g:
 3 , 4 
x1
3 x  2  12
8.1. Defina, analiticamente, a função g sem utilizar módulos.
8.2. Indique, justificando, o valor lógico de cada uma das proposições.
8.2.1. A função g tem dois zeros reais distintos.
8.2.2. O contradomínio da função g é  12 ,   .
8.2.3. A função g tem três extremos.
8.3. Resolva a condição g  x   3 .
Apresente o conjunto-solução usando a notação de intervalos de números reais.
9. Na figura está representado um retângulo [ABCD].
Este retângulo é o esboço de um azulejo de 30 cm de comprimento por 18 cm de largura
eque será constituído por uma parte colorida e por uma parte branca.
A parte colorida é formada por quatro quadrados iguais e um retângulo, tal como a figura
sugere.
Cada quadrado tem um vértice num vértice do retângulo [ABCD].
Seja x o lado de cada um destes quadrados, medido em cm  x  0 , 9  .
9.1. Mostre que a área, em cm2, da parte colorida do azulejo é dada, em função de x, por:
A  x   8x 2  96x  540
9.2. Determine o valor de x para o qual a área da parte colorida do azulejo é mínima e calcule
essa área.
9.3. Determine os valores de x para os quais a área da parte colorida do azulejo é inferior à
área da parte branca do azulejo.
Ficha de preparação para o teste de avaliação 5
10. Considere as funções f e g definidas por:
f  x   4  4x 2
e g x  x 1
10.1. Determine o domínio de cada uma das funções f e g.
10.2. Determine o domínio da função h  f  g e determine os zeros de h.
 1
10.3. Mostre que  f g     3 .
2
11. Na figuras estão representadas duas funções f e g.
11.1. Indique o domínio e o contradomínio de cada uma das funções.
11.2. Indique o domínio da função f  g e calcule  f  g  0  .
11.3. Defina analiticamente cada uma das funções.
11.4. Indique o domínio de f  g e calcule  f  g  3  .
12. Considere a função real de variável real f, definida em  , 1 , por:
f  x   4  1 x
( f 1 é a função inversa da função f .)
12.1. Calcule f 1 1  f 1  2 .
12.2. Caracterize a função f 1 .
Teste de avaliação 5 (90 min)
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
Professor
/20
N.º
Matemática A | 10.º ano
Data
/
/20
1. Seja f a função, de domínio  2 ,   , definida por f  x   x  2 .
Qual é o valor de f 1  4  ( f 1 é a função inversa de f )?
(A) 18
(B) 2
2. Seja h a função, de domínio
definida por g  x  
(C) 16
(D) 4
, definida por h  x   x  3 . Seja g a função de domínio
1
2 2
. Para um certo número real a, tem-se que  g h  a  
.
2
x 1
Qual é o valor de a?
(A) 2  2
(B) 2 2
(C)
(D) 2  2 2
2
3. Dado um plano munido de referencial ortogonal, a translação  do plano que ao ponto
P  x , y  associa o ponto P   x , ay  designa-se por:
(A) contração vertical de coeficiente a se a  1 ;
(B) dilatação vertical de coeficiente a se a  1 ;
(C) contração horizontal de coeficiente a se 0  a  1 ;
(D) dilatação horizontal de coeficiente a se a  1 .
4. Na figura está representado, num plano munido de um referencial
cartesiano, o gráfico da função afim f.
Considere a função h, tal que, para todo x  Dh , h  x   f   x  .
O conjunto-solução da condição f  x   h  x  é:
(A)
 , 0
(B)
2 ,  
(C)
5. Considere a função j definida por:
 ,  2
j:
(D) 0 ,  
 2 , 5 
x1
Qual das seguintes afirmações é verdadeira?
(A) O contradomínio da função j é 8 , 50  .
(B) A função j é par.
(C) A função j tem um mínimo absoluto para x  2 .
(D) A função j não é par nem ímpar.
2x 2
\ 1
Teste de avaliação 5 (90 min)
6. De uma função quadrática f, de domínio
, sabe-se que 2 e 6 são os seus zeros.
Qual dos seguintes pontos não pode pertencer ao gráfico da função f ?
(A)
0 , 4
(B)
 4 , 0
(C)
 4 , 1
(D)
1, 4 
7. Na figura está representada, num plano munido de um referencial ortonormado, parte do
gráfico da função f de domínio
, definida por f  x   x  a  b  a , b 
.
Qual das seguintes afirmações é verdadeira?
(A) a  0  b  0
(B) a  0  b  0
(C) a  0  b  0
(D) a  0  b  0
8. Considere as funções h e j definidas, respetivamente, por h  x  
j  x   3 x  2 em
4
2x
em
\
 2 e
.
Admita que a   h j  10  e b  j 1  1 .
Qual é o valor de a  b ?
(A) 2 2  4
(B) 4 2  12
(C) 2 2  4
(D) 4 2  12
9. Considere a função afim f que, para dados valores reais m  0 e b, é definida por
f  x   mx  b .
Sabe-se, fixado um referencial ortonormado do plano, que:
● o ponto A 1, 2  pertence ao gráfico de f;
● o ponto B  2 , 3  pertence ao gráfico de f.
Caracterize a função f 1 , função inversa de f.
10. Considere a função f definida em
por f  x   x 2  2x .
Estude a função f quanto à paridade.
Teste de avaliação 5 (90 min)
11. Na figura está representado, num referencial ortonormado, o gráfico da função g.
11.1. Indique o domínio e o contradomínio da função g.
11.2. Construa uma tabela de variação para a função g.
11.3. Considere a função f definida por f  x   g  x  1  1.
11.3.1. Esboce o gráfico da função f.
11.3.2. Estude a função f quanto à monotonia.
12. Considere a função h definida em
por h  x   6  2x  2 .
12.1. Determine o contradomínio da função h.
12.2. Determine os zeros da função h.
12.3. Resolva, em
, a condição h  x   4 .
Apresente o conjunto-solução usando a notação de intervalos de números reais.
13. Resolva as seguintes equações, simplificando tanto quanto possível as expressões que
representam as respetivas soluções.
13.1.
2x  2  1  x
13.2.
x 3 3 x
14. Na figura está representada, num referencial ortonormado,
parte do gráfico da função polinomial, do terceiro grau, g,
definida em .
14.1. Determine o domínio da função h tal que h  x   g  x  .
14.2. Prove que a função g pode ser definida por:
g x 
x3 x2

 4x  6
2
2