x + 2

Lista de Exercícios
Aluno(a):_______________________________________Nº.____
Pré Universitário
Uni-Anhanguera
Professor: Vinícius Camargo
Disciplina: Matemática
Série: 8º ano
Data da prova: 15/09
1) Resolva os produtos notáveis
a)
a b
 + 
 b a
2
b) (x3y2z4 + 2a)2
c) (5x – 4x)2
d) (2x + 3y) • (2x – 3y)
e) (x – 5) • (x – 3)
f)
(x + 5) • (x – 2)
g) (x + 2)3
h) (2x – y)3
i)
Que termo devemos adicionar à expressão
4x8 – 6x4y + 9y2 para que ela represente o quadrado de uma soma?
a) 6x4y
b) 12x4y
c) 18x4y
d) 24x4y
2) Sendo a2 + b2 = x e ab = y, então (a + b)2 é igual a:
a) x2
b) x + y
c) x – 2y
d) x2 + 2y
e) x + 2y
3) Das alternativas abaixo, uma é FALSA. Identifique-a.
a) (a + b)2 = a2 + 2ab + b2
b) a2 – b2 = (a – b) • (a + b)
c) a3 – b3 = (a – b) • (a2 + ab + b2)
d) a2 + b2 = (a + b)2 – 2ab
e) a3 + b3 = (a + b) • (a2 – 2ab + b2)
4) Sendo a + b = 4 e a – b = 2, calcule o valor de a2 – b2.
5) Aplicando as regras dos produtos notáveis, desenvolva:
a)
b)
i)
e)
f)
g)
2
(3x + y )
h)
(1 + 5m) (1 − 5m)
(ab − c )2
(m − 1)3
(a
3
)(
− b 3 a 3 + b3
2
y

x− 
2
j) 
3
k) (a + t )
3
2
3
2
l) a c − b a c + b
2 2
c)
d)
(10 + a x )(10 − a x )
2
( x + 8)2
(2 − 3a )2
(
)(
2
)
(4 + h )2
6) Simplifique as expressões algébricas:
)
m) ( y + 2xy )
k
2 k
2
 + p  − p 
3

n)  3
o)
p)
q)
(x − y )2 − x( x − 2 y )
(x − 2)2 + a(3a + 2)
(m + 1) (m − 1) + (m + 1)2 − 2m
(x + a )(x − a ) + a (a
2
r)
2
2
2
)
−1
Aplique a regra para desenvolver os produtos notáveis:
a) ( 3x + 5)2
R: 9x2 + 30x + 25
b) ( 2x – 3y)2
R: 4x2 –12xy + 9y2
c) ( 5a2 + 1 )2
R: 25a4 + 10a2 + 1
1

 x + 3

d)  2
 2x 1 
− 

3
2

e)
2
1 2
x + 3x + 9
R: 4
2
4x2 2x 1
−
+
3 4
R: 9
f) (x+9) (x-9)
R: x2 – 81
g) (-5x - 2) 2
R: 25x2+20x+4
 x y
− + 
h)  2 3 
2
2

 − 3x − 
3
i) 
2
x 2 xy y 2
−
+
3
9
R: 4
4
R: 9x + 4x + 9
2
3
 3x
 3 x

 + y  − y 
 4

j)  4
9x 2
− y2
R: 16
10) Simplifique as expressões utilizando os produtos notáveis:
a) x(3x-2)+(x+3)2
b) (7x+6)2 – 6x (x+14)
c) (a - 2)(a - 5) – (a + 5)2
d) (9y + 1)2 – (y + 9)2
e) (2a + 3b)2 - 4a(a + 3b)
f) 2x(x - 3)2 + 4x(3x - x2)
g) x(x - 1)2 – x2 (x + 1)
h) (a - b)2 – (a + b)(a - b)
i)
(3x + 7)2 + (x - 3)2
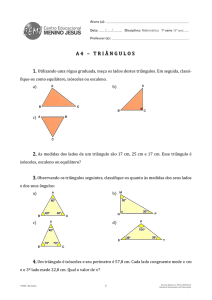
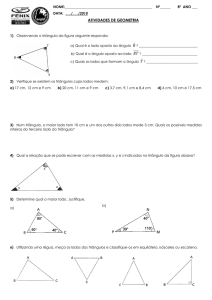
1)
Qual a relação que se pode escrever com as medidas x, y e z indicadas no triângulo da figura
abaixo?
2)
a)
Determine qual o maior lado. Justifique.
b)
3)
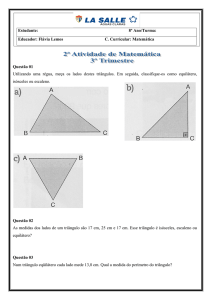
Utilizando uma régua, meça os lados dos triângulos e classifique-os
classifique os em equilátero, isósceles
ou escaleno.
4
4)
Observe os triângulos e classifique-os
classifique os em acutângulo, retângulo ou obtusângulo. Utilize o
transferidor se necessário.
5)
Observe os triângulos seguintes e classifique-os
classifique os quanto aos lados e quanto aos ângulos.
6)
Nas figuras abaixo, determine o valor de x:
5
7)
Determine a medida dos ângulos internos dos triângulos isósceles, observando a congruência
dos lados.
8)
O ∆ ABC é isósceles, sendo AB ≅ AC . Sabendo que seu perímetro é 15,6 cm, determine o
valor de x.
9)
Em um triângulo isósceles, um dos ângulos da base mede 25°. Quais as medidas dos três
ângulos do triângulo?
6
10)
Num triângulo isósceles, um dos ângulos mede 120°. Calcule a medida dos outros dois
ângulos desse triângulo.
11)
Considere as afirmações:
I – Todo triângulo equilátero é acutângulo.
II – Todo triângulo escaleno é obtusângulo.
III – Um triângulo retângulo pode ser isósceles.
Assinale a opção correta. Justifique.
a) ( ) todas as afirmações são verdadeiras.
b) ( ) todas as afirmações são falsas.
c) ( ) apenas a afirmação I é verdadeira.
d) ( ) apenas a afirmação III é verdadeira.
e) ( ) apenas a afirmação II é falsa.
7