Capítulo 2 - Hidrodinâmica Para se descrever o escoamento

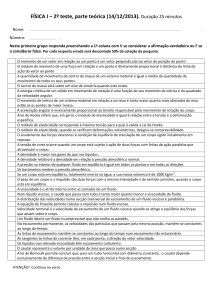
Capítulo 2 - Hidrodinâmica
Para se descrever o escoamento de um fluido usa-se, comumente, o método de
Euler que fixa um ponto do fluido e acompanha a evolução da velocidade com
o tempo
Chamamos de linha de corrente à tangente ao vetor velocidade.
Dizemos que o escoamento é Estacionário quando o campo de velocidades não
depende mais explicitamente do tempo, isto é,
Neste regime estacionário, as linhas de corrente coincidem com as trajetórias
das partículas do fluido.
Equação da Continuidade
Consideremos um escoamento estacionário. A massa do fluido que atravessa com
velocidade um tubo de área
num intervalo de tempo
tem que passar pelo
tubo com velocidade , área
no mesmo intervalo de tempo . Logo,
A equação (1) é chamada de Equação da Continuidade (válida para escoamento
estacionário).
Se o fluido é incompressível então
e
Se o escoamento não é estacionário, temos que considerar um volume fixo do
fluido limitado por uma superfície fechada . Seja o versor normal externo
num ponto cuja área innifinitesimal é .
1
A massa que atravessa
para fora num intervalo de tempo
é
O fluxo de massa de fluido por unidade de tempo através da superfície fechada é
então
A massa total de fluido contida no volume
num dado instante de tempo é
A massa
contida no volume pode variar no tempo, mas como a massa não
pode ser criada nem destruída, essa variação da massa só pode ser resultante do
fluxo através da superfície fechada que envolve . Se
aumenta (diminui),
então entra (sai) mais fluido do que sai (entra) através dessa superfície.Ou seja,
onde o sinal negativo aparece pois quando o fluxo para fora é positivo, a massa
diminui, isto é,
A equação (3) é a equação da continuidade no formato integral. No formato,
diferencial ela se escreve
2
onde
definido por
é o operador divergente de um vetor
,,
Fluido em Movimento
Um elemento infinitesimal de massa
com volume infinitesimal
movimento descrito pela 2ª. Lei de Newton
tem seu
onde somamos vetorialmente as contribuições superficiais e volumétricas.
Inicialmente, desprezaremos entre as forças volumétricas aquelas oriundas do
atrito entre camadas que correspondem a existências de forças viscosas.
Chamaremos de fluido ideal ou fluido perfeito ao fluido com viscosidade nula.
Equação de Bernoulli
Vamos supor um fluido ideal e incompressível num escoamento estacionário.
Consideremos um tubo de corrente muito estreito (para podermos definir energia
potencial gravitacional) limitado pelas secções transversais
nos pontos 1
e 2 , onde as pressões são
e as velocidades
.
Durante um intervalo de tempo
o fluido se desloca para os pontos 1´ e 2´.
Da equação da continuidade, temos
A variação da energia cinética será
3
Pelo teorema de trabalho-energia, a variação da energia cinética é igual ao
trabalho realizado pela força resultante que, neste caso, é a soma de 2 fo rças: a
de pressão e a gravitacional.
Para empurrar o fluido para dentro do tubo de corrente o trabalho realizado sobre
o sistema (isto é, sobre o elemento infinitesimal de fluido de massa
), na
extremidade de entrada, vale:
. O trabalho realizado pelo sistema
(para empurrar o fluido que está adiante) na extremidade de saída vale: :
. Logo, o trabalho da pressão para movimentar o fluido será
O trabalho realizado pela força gravitacional é o contrário da variação de energia
potencial (
Logo,
Utilizando (5), temos
Logo,
A equação acima é a chamada Equação de Bernoulli, derivada por Daniel
Bernoulli em 1738.
A Fórmula de Torricelli
Seja um reservatório de área muito maior do que a área no orifício de saída
(ponto O) e que está a uma altura deste ponto O. Tanto a área aberta quanto o
orifício em O estão abertos para a atmosfera.
4
Como
e
, podemos desprezar o termo em
Donde, a velocidade de saída pelo orifício O será
.
Tubo de Pitot
Muito utilizado para medir a velocidade de um avião. Na figura abaixo vemos o
que acontece quando um objeto, com boa aerodinâmica como uma asa de avião,
está imerso num fluido que escoa num regime estacionário.
A velocidade sobre o perfil é e no ponto O a velocidade é praticamente zero, o
ponto O é chamado ponto de estagnação.
Abaixo vemos um esquema do tubo de Pitot. Se a pressão em A é p e em O é p 0 a
velocidade em A é v e em O é v0=0 e ambos estão praticamente à mesma altura
então
Acoplado ao manômetro com um fluido de densidade
que sobe uma altura
Donde obtemos a velocidade do avião
5
Fenômeno de Venturi
Consideremos um fluido incompressível escoando estacionariamente por uma
canalização horizontal (veja fig.). Há um estrangulamento do tubo no ponto 2.
Desprezando as pequenas variações de altura, teremos
Se
e
forem as áreas dos tubos em 1 e 2
continuidade,
. logo,
, teremos, da eq. da
Ou seja, pode-se utilizar o fenômeno de Venturi para se calcular a velocidade de
escoamento de um fluido num tubo.
A diminuição da pressão no estrangulamento é o mesmo efeito que soprar entre 2
folhas de papel: elas tenderão a grudar uma na outra.
Circulação
Uma grandeza importante para caracterizar um escoamento de um fluido é a
Circulação
ao longo de uma integral de linha ou de circuito fechado ,
definida por
6
1) Um recipiente cilíndrico em rotação com velocidade angular
logo,
2) Se
para um círculo com um raio
qualquer então
bem diferente do caso anterior quando
É o que acontece, aproximadamente, quando um fluido escoa pelo ralo de
uma banheira.
Usando a eq. de Bernoulli
em cuja superfície isobárica
uma singularidade em
Funil !!
, teríamos
o que geraria
No mundo real, a isobárica tem forma de um
7
Escoamentos Rotacionais e Irrotacionais
A circulação tem propriedades aditivas. Na fig 2.17 abaixo, temos
De maneira que podemos pensar em subdividir o circuito Γ como a soma de
microcircuitos (fig 2.18) e a circulação se transforma em cálculo num ponto !
Na fig 2.19 vemos o circuito ABCDA. Ambos os casos estudados acima 1) e 2)
tem
. Nos 2 casos,
nos trechos AB e CD. No trecho BC
temos
e no trecho DA
.
Para o caso 1)
como
é a área infinitesimal do circuito Γ=ABCDA, então
Para o caso 2)
e
Note que a circulação calculada acima não incluiu a origem r = 0 !! (mas
)
Portanto se o escoamento é irrotacional
pelo teorema de Stokes
8
Efeito Magnus
Na figura (a) vemos o escoamento uniforme de um fluido através do cilindro.
A velocidade é maior onde as linhas de corrente estão mais juntas (eq. da
continuidade...área menor velocidade maior).
Se o cilindro começa a rodar, o ar começa a girar como mostra a fig (b). O
resultado da composição é mostrado na fig (c). Como a velocidade é maior na
parte de cima do que em baixo do cilindro, há uma pressão empurrando o
cilindro para cima. Se invertermos a rotação, também inverte o empuxo. Esse
efeito foi estudado primeiramente por Magnus em 1853. Sobre uma esfera é o
responsável pelo top spin, slice e side spin do tênis e pela folha seca e curva no
futebol.
O empuxo aerodinâmico é o responsável pela sustentação do avião. Na figura
abaixo vemos um perfil de uma asa de avião
Se o escoamento deixa de ser lamelar (altas velocidades), surgem turbilhôes e
vórtices que desestabilizam o vôo.
Em 1869, Lord Kelvin enunciou que: No escoamento de um fluido ideal
homogêneo, sujeito apenas a forças conservativas, tem-se a conservação
temporal da circulação
Logo, se o escamento é iniciado a partir do repouso então o escoamento será
sempre irrotacional.
Num vórtice ou turbilhão a velocidade v é tipicamente
Podem surgir ainda anéis de vórtices
9
Viscosidade
A viscosidade é uma força volumétrica de atrito de deslizamento entre camadas
de um fluido.
Consideremos um fluido contido entre duas placas planas paralelas de área A e
espaçamento d.
A experiência mostra que se puxarmos a placa superior com força ela se
desloca com velocidade constante
de modo que a força viscosa é igual e
contrária a .
Também o experimento revela que o fluido em contacto com as placas (superior
ou inferior) adere e se movimenta com a mesma velocidade. Assim, a placa
superior (inferior) se movimenta com velocidade
(zero). Então a velocidade
depende linearmente de y,
A lei de Newton da viscosidade é definida (em módulo)
A constante é chamada coeficiente de viscosidade e sua dimensão é N.s/m2
Usa-se o centipoiseque é um centésimo de 1 poise
Essa constante
varia de um fluido para outro, é maior para fluido mais
‘espesso’ e depende fortemente da temperatura. A 200 C a água tem
O escoamento viscoso é rotacional como pode ser visto na Fig.2.27 abaixo. No
retângulo mostrado, a circulação nos lados verticais 2 e 4 é zero pois a
velocidade é perpendicular ao deslocamento e nos lados 1 e 3 teremos
e como
então a circulação é positiva no sentido horário.
10
A lei de Hagen-Poiseuille
Suponhamos um fluido escoando com velocidade não muito alta (regime
lamelar) num tubo cilíndrico cuja secção transversal tem raio a. A velocidade do
fluido na primeira camada em contacto com a parede do tubo é zero e cresce
atingindo seu máximo no centro da secção transversal.
Na figura abaixo, focamos uma camada cilíndrica de raio r e comprimento l. A
diferença de pressão nos pontos 1 e 2 multiplicado pela área nos dá a força que
movimenta horizontalmente o fluido
A camada em questão provoca uma tensão superficial na área tangencial
igual a
Lembrando que
escrevemos a Lei de Newton da viscosidade
Donde
Integrando e lembrando que
, teremos
O perfil de velocidades é parabólico !
11
A vazão
pode agora ser calculada:
ou seja,
A equação acima é a lei de Hagen-Poiseuille.
Efeitos da Viscosidade
Importante lembrar que a equação de Bernoulli, efeito Magnus, etc foram
analisados para um fluido ideal num escoamento estacionário. Pode-se
demonstrar que um fluido escoando nestas circunstâncias é irrotacional.
Teremos então a hidrodinâmica clássica.
No mundo real, porém, há a inevitável a presença da viscosidade. Como vimos
acima, isso leva ao escoamento rotacional. Quando um objeto se move num
fluido real, forma-se, nas primeiras camadas de contacto entre o fluido e o objeto,
uma camada limite no interior da qual o escoamento é rotacional e, afastando-se
dessa camada limite, a descrição clássica irrotacional volta a ser uma boa
aproximação.
Na figura abaixo vemos uma esfera se movendo em alta velocidade num fluido.
Vemos que a camada limite se descola da superfície formam vórtices. O regime
entra então num regime turbulento de difícil descrição e análise.
12