Aula 09 Representação de Funções de 1º Grau – Plano Cartesiano

Matemática Aplicada a Informática
Profª Rita de Cassia Gaieski
[email protected]
Aula 09
Representação de Funções de 1º Grau – Plano Cartesiano
A representação desse modelo de função no plano cartesiano é dada por uma reta
crescente ou decrescente. A posição da reta no plano depende do valor do coeficiente
angular a, caso ele seja positivo (a > 0), a reta é crescente; e se for negativo (a < 0), a
reta é decrescente. O coeficiente representado por b é denominado linear e indica em
que ponto do eixo y (ordenada) a reta passa. O gráfico da função é construído no plano
de coordenadas cartesianas, onde cada valor de x (eixo das abscissas) possui uma
representação em y (eixo das ordenadas).
Função do 1º grau crescente – (a > 0):
A função y = 2x + 5 é representada por uma reta crescente, pois o coeficiente angular é
positivo, possuindo valor igual a 2. Veja o gráfico:
Matemática Aplicada a Informática
Profª Rita de Cassia Gaieski
[email protected]
Na função crescente, à medida que os valores de x aumentam os valores de y também
aumentam; ou à medida que os valores de x diminuem, os valores de y diminuem.
Função do 1º grau decrescente – (a < 0):
A função y = –2x +3 é representada por uma reta decrescente, pois o coeficiente angular
é negativo, possuindo valor igual a –2. Veja o gráfico:
Na função decrescente, à medida que os valores de x aumentam, os valores de y
diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam.
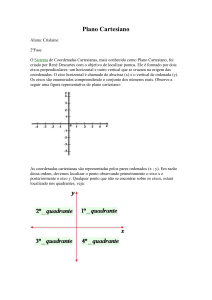
Plano Cartesiano
O eixo horizontal é chamado de abscissa (x) e o vertical de ordenada (y). Os eixos são
enumerados compreendendo o conjunto dos números reais.
As coordenadas cartesianas são representadas pelos pares ordenados (x ; y). Em razão
dessa ordem, devemos localizar o ponto observando primeiramente o eixo x e
Matemática Aplicada a Informática
Profª Rita de Cassia Gaieski
[email protected]
posteriormente o eixo y. Qualquer ponto que não se encontrar sobre os eixos, estará
localizado nos quadrantes:
1º quadrante = x > 0 e y > 0
2º quadrante = x < 0 e y > 0
3º quadrante = x < 0 e y < 0
4º quadrante = x > 0 e y < 0
Localizando pontos no Plano Cartesiano:
A(4 ; 3) → x = 4 e y = 3
B(1 ; 2) → x = 1 e y = 2
C( –2 ; 4) → x = –2 e y = 4
D(–3 ; –4) → x = –3 e y = –4
E(3 ; –3) → x = 3 e y = –3