Lei de Gauss

UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
DISCIPLINA: FÍSICA 3
2a Lista de Exercícios
Lei de Gauss
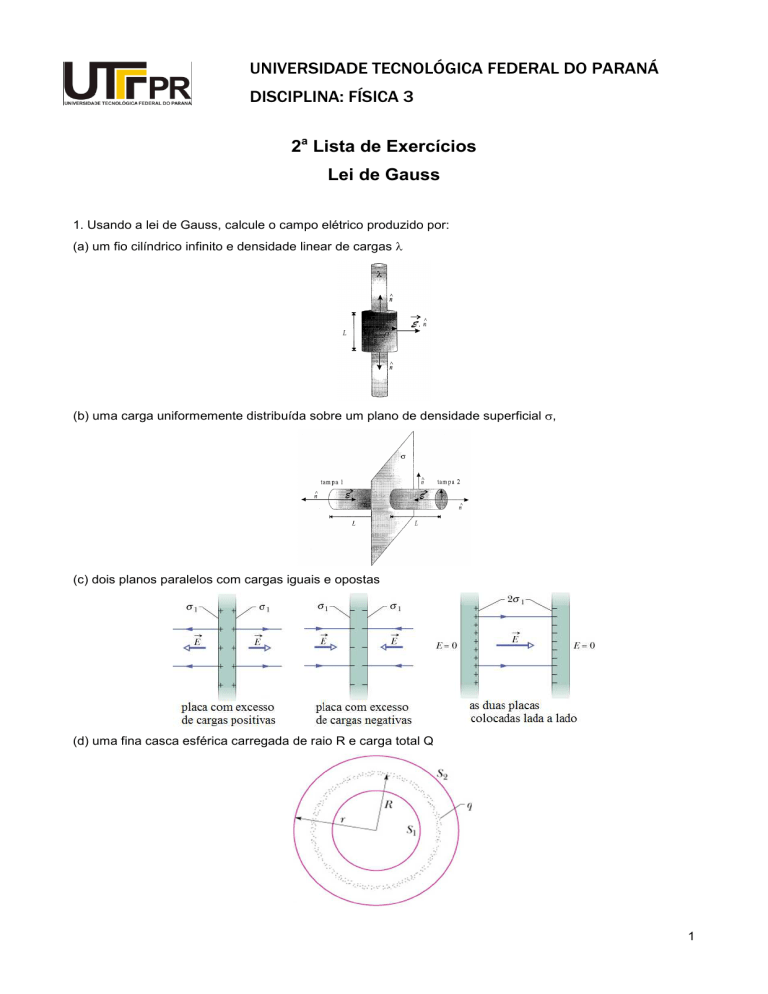
1. Usando a lei de Gauss, calcule o campo elétrico produzido por:
(a) um fio cilíndrico infinito e densidade linear de cargas λ
(b) uma carga uniformemente distribuída sobre um plano de densidade superficial σ,
(c) dois planos paralelos com cargas iguais e opostas
(d) uma fina casca esférica carregada de raio R e carga total Q
1
(e) uma esfera sólida uniformemente carregada que tem raio R
e uma carga total Q, distribuída uniformemente através do
volume da esfera cuja densidade de carga é ρ=Q/V onde
V = 4 / 3πR 3 é o volume da esfera.
Resp: (a)
E=
Para:r> R E =
λ
2πε 0 r
(b)
E=
σ
2ε 0
(c) E = 0 ,0 para x<0 e x>d e E =
σ ˆ para 0<x<d (d) Para:r> R
Q , r<R, E = 0 (e)
i
E=
ε0
4πε 0 r 2
Q
Q , r<R,
E=
r
4πε 0 r 2
4πε 0 R 3
2. Considerar a superfície cúbica fechada de aresta a, com vértice na origem dos eixos coordenados XYZ.
Esta superfície está colocada em uma região onde existe um campo elétrico paralelo ao eixo X. Achar o
fluxo através da superfície e a carga total em seu interior se o campo é:
(a) Uniforme. (b) Varia segundo
E = C.x, onde C é uma constante. Resp: (a) 0 e (b) φ = Q / ε 0
3. Uma esfera não condutora de raio R1 tem uma cavidade esférica de raio R2 cujo centro coincide com o da
esfera. Achar o campo elétrico em pontos fora da esfera, no interior da esfera e na cavidade. Faça os
gráficos do campo em função da distância ao centro e encontre a carga sobre as superfícies interna e
externa do condutor, considerando que. (a) Uma carga Q está uniformemente distribuída em seu volume.
(b) Além da carga na esfera existe no centro da cavidade uma carga q. (c) Discuta o caso onde a esfera
seja condutora Resp: (a) Para:r> R1 E =
E=
q
4πε 0 r
r<R2,
E=
, R1<r< R2
2
E=
(
Q
4πε 0 r
2
, r<R2, E = 0 , R1<r< R2
E=
(
)
ρ
3
r 3 − R2 (b) r> R1,
3ε 0 r 2
E=
(Q + q ) ,
r<R2,
4πε 0 r 2
)
Q , r<R2, E = 0 , R1<r< R2 E = 0 (b) r> R1,
 Q r 3 − R2 3
 , (c) (a) Para:r> R1
(Q + q ) ,
E=
E=
+ q
2
 3
3
4
πε
4πε 0 r 2
4πε 0 r  R1 − R2
0r

1
2
q , R1<r< R2 E = 0
4πε 0 r 2
4. Uma carga puntiforme é colocada no centro de uma superfície Gaussiana esférica. Diga em qual dos
casos abaixo haverá alteração do valor do fluxo ΦE. (a) A esfera é substituída por um cubo de mesmo
volume. (b) Idem, por um cubo de volume dez vezes menor. (c) A carga é deslocada do centro da esfera
para outro ponto, ainda no seu interior. (d) A carga é retirada para fora da esfera. (e) Uma segunda carga é
colocada próximo, porém do lado de fora da esfera. (f) Idem, colocada dentro da esfera.
5. Considere uma “casca'' esférica condutora, de raio b e carga –Q<0, concêntrica a uma esfera condutora
maciça, de raio a<b e carga +Q, conforme mostra a figura abaixo. a) Usando a Lei de Gauss, calcule o vetor
campo elétrico,
r
E , em todo o espaço.
Resp: Para: a<r<b Er =
Q
rˆ , r<a E = 0 , r>b E = 0
4πε 0 r 2
2