Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 28 – O CAMPO ELÉTRICO
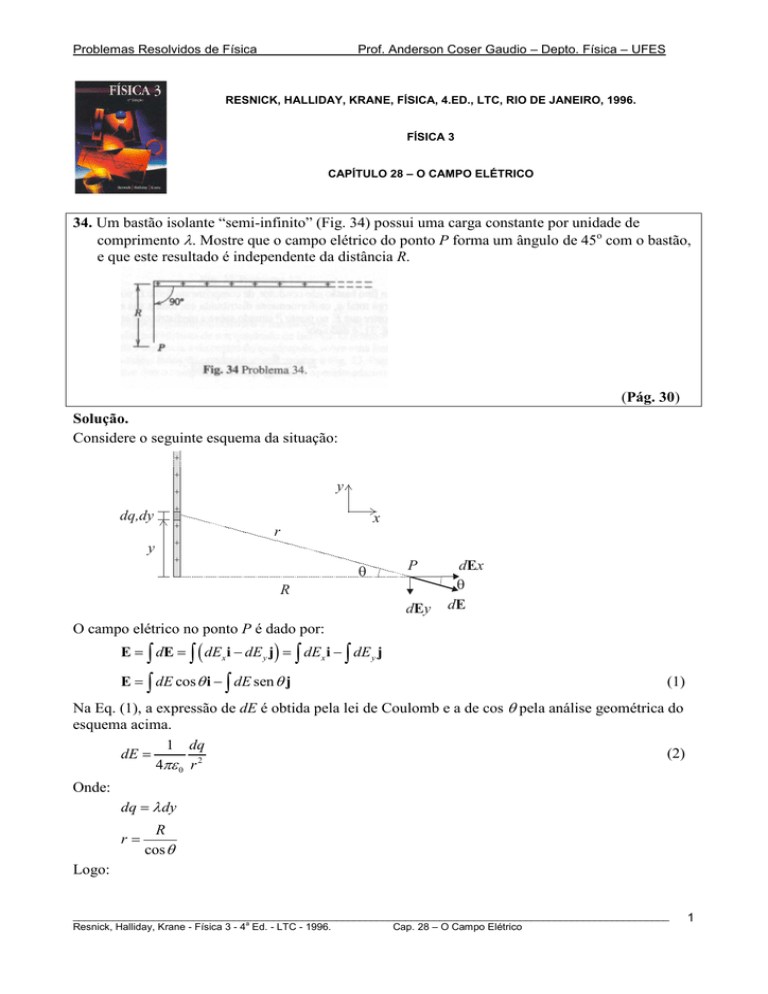
34. Um bastão isolante “semi-infinito” (Fig. 34) possui uma carga constante por unidade de
comprimento λ. Mostre que o campo elétrico do ponto P forma um ângulo de 45o com o bastão,
e que este resultado é independente da distância R.
(Pág. 30)
Solução.
Considere o seguinte esquema da situação:
+
+
y
+
dq,dy
y
+
+
+
x
r
+
θ
P
R
dEy
dEx
θ
dE
O campo elétrico no ponto P é dado por:
E =∫ dE =∫ ( dEx i − dE y j) =∫ dEx i − ∫ dE y j
=
E
∫ dE cos θ i − ∫ dE sen θ j
(1)
Na Eq. (1), a expressão de dE é obtida pela lei de Coulomb e a de cos θ pela análise geométrica do
esquema acima.
1 dq
(2)
dE =
4πε 0 r 2
Onde:
dq = λ dy
r=
R
cos θ
Logo:
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
1
Problemas Resolvidos de Física
dE =
Prof. Anderson Coser Gaudio – Depto. Física – UFES
1 cos 2 θλ dy
4πε 0
R2
(3)
Podemos determinar uma expressão para dy partindo-se da relação:
y = R tan θ
Derivando-se y em relação à θ:
R
dy =
dθ
cos 2 θ
Substituindo-se (4) em (3):
1 λ
dE =
dθ
4πε 0 R
(4)
(5)
Substituindo-se (5) em (1):
π /2
λ
1 λ π /2
θ
θ
cos
d
sen θ dθ j = (1i − 1j)
E=
i
−
∫
∫
0
0
4πε 0 R
4πε 0 R
(
=
E
)
λ
λ
i−
j
4πε 0 R 4πε 0 R
Como as componentes i e j do vetor E são iguais, o ângulo θ é 45o. Este resultado não depende de
R, pois este termo está igualmente presente em ambas as componentes de E.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
2