Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 28 – O CAMPO ELÉTRICO
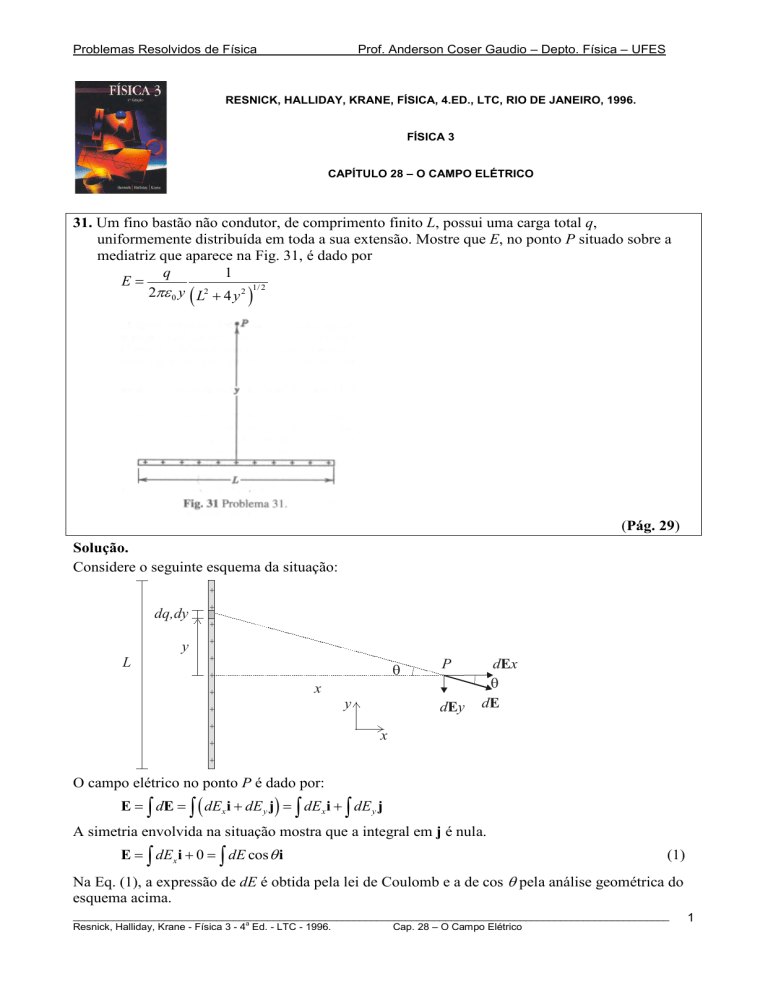
31. Um fino bastão não condutor, de comprimento finito L, possui uma carga total q,
uniformemente distribuída em toda a sua extensão. Mostre que E, no ponto P situado sobre a
mediatriz que aparece na Fig. 31, é dado por
q
1
E=
2πε 0 y ( L2 + 4 y 2 )1/ 2
(Pág. 29)
Solução.
Considere o seguinte esquema da situação:
+
dq,dy
y
L
+
+
+
+
θ
+
+
P
x
+
+
+
y
dEy
dEx
θ
dE
x
+
O campo elétrico no ponto P é dado por:
E =∫ dE =∫ ( dEx i + dE y j) =∫ dEx i + ∫ dE y j
A simetria envolvida na situação mostra que a integral em j é nula.
=
E
∫ dE i +=0 ∫ dE cos θ i
x
(1)
Na Eq. (1), a expressão de dE é obtida pela lei de Coulomb e a de cos θ pela análise geométrica do
esquema acima.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
1
Problemas Resolvidos de Física
dE =
1
Prof. Anderson Coser Gaudio – Depto. Física – UFES
dq
4πε 0 ( x + y 2 )2
2
cos θ =
(x
x
2
+ y2 )
1/ 2
Logo:
E=∫
1
xdq
4πε 0 ( R 2 + x 2 )3 / 2
(2)
i
A expressão de dq é obtida por meio da densidade linear λ de carga do bastão.
q dq
λ= =
L dy
q
dy
L
Substituindo-se (3) em (2):
1 qx + L / 2
dy
1 qx + L / 2
dy
2∫
E =
i
i
3/ 2
3/ 2
∫
−
/
2
0
L
2
2
2
4πε 0 L
4πε 0 L
(x + y )
( x + y2 )
dq =

1 qx 
y
E=
2
2
2πε 0 L  x ( x + y 2 )1/ 2

E=
q
1
2πε 0 x ( 4 x + L2 )1/ 2
2
(3)
+L/2
i
0
i
Podemos verificar facilmente que esta expressão se reduz à lei de Coulomb quando afastamos o
ponto P do bastão para distâncias muito maiores do que seu comprimento (x >> L).
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
2