L - Anglo

1) [UnB-MODIFICADA] Cada estrutura lateral
de uma torre metálica, em forma de uma
pirâmide regular de base quadrada, consiste
de um triângulo isósceles ABC, de base BC,
conforme representado na figura adiante.
Para minimizar o número de peças de
tamanhos distintos na fabricação da torre, as
barras metálicas BC, CD, DE, EF e FA têm
comprimentos iguais. Calcule a medida do
ângulo BÂC.
2) A soma das medidas dos cinco ângulos
assinalados na figura abaixo é:
a) 90
b) 150
c) 180
d) 270
e) 360
3) No triângulo a seguir, os segmentos BB1;
B2B3; B4B5; B6B7; ..., são todos paralelos
entre si, e os segmentos AB; B1B2; B3B4;
B5B6; ..., também são paralelos entre si.
Sabendo que:
i) O triângulo ABB1 é eqüilátero, de lado c.
ii) BC mede a.
iii) AC mede b.
Calcule a medida da linha poligonal
formada pelos segmentos AB BB1 B1B2
B2B3 B3B4...BnC, com n tendendo ao
infinito.
4) [UNESP-08] Uma certa propriedade
rural tem o formato de um trapézio
como na figura. As bases WZ e XY do
trapézio medem 9,4 km e 5,7 km,
respectivamente, e o lado YZ margeia
um rio.
Se o ângulo XYZ é o dobro do ângulo
XWZ, a medida, em km, do lado YZ que
fica à margem do rio é:
a)
b)
c)
d)
e)
7,5.
5,7.
4,7.
4,3.
3,7.
5)
No trapézio da figura, PN = PQ.
Então o ângulo  mede:
a) 64
b) 68
c) 72
d) 76
e) 80
6)
Na figura abaixo, A, B, C são pontos
de tangência. Então x vale:
a) 3/16
b) 1/8
c) 3/32
d) 1/32
e) 1/16
7) [FUVEST-MODIFICADO] Na figura a
seguir, ABCD, é um quadrado com 24cm
de perímetro, e os pontos M e D, são
pontos médios dos segmentos, AB e BE,
respectivamente. Calcule a medida dos
segmentos AN e ND.
8)[UNICAMP]
Três
canos
de forma
cilíndrica e de mesmo raio r, dispostos
como indica a figura adiante, devem ser
colocados dentro de outro cano cilíndrico
de raio R, de modo a ficarem presos sem
folga. Expresse o valor de R em termos de
r para que isso seja possível.
(DICA: calcule a altura do triângulo
eqüilátero)
9)[UNICAMP] Para calcular a circunferência
terrestre, o sábio Erastóstenes valeu-se da
distância conhecida de 800km entre as
localidades de Alexandria e Siena no Egito (A e
S respectivamente), situadas no mesmo
meridiano terrestre. Ele sabia que, quando em
Siena os raios solares caíam verticalmente, em
Alexandria eles faziam um ângulo de 7,2 com a
vertical.
Calcule,
com
esses
dados,
a
circunferência terrestre, isto é, o comprimento
de uma volta completa em torno da Terra.
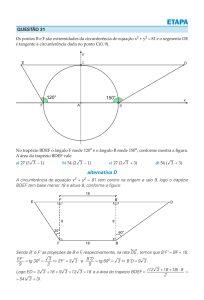
10) [UNESP] Os pontos A, B, C, D, E e F
pertencem à circunferência. O valor de 
é:
a) 60
b) 50
c) 45
d) 40
e) 35
11) [UNESP] Em um quadrilátero ABCD
tem-seAB = AC = AD, conforme a figura
abaixo. Sabe-se que o ângulo BÂC mede
20. Então o ângulo BDC mede:
a) 5
b) 10
c) 15
d) 20
e) 40
12) [UNIFESP-08] A soma de n - 1 ângulos
internos de um polígono convexo de n
lados é 1900°. O ângulo remanescente
mede:
a) 120°.
b) 105°.
c) 95°.
d) 80°.
e) 60°.
.
13) [FGV] Na figura, ABC é um triângulo
com AC = 20 cm, AB = 15 cm e BC = 14
cm. Sendo AQ e BP bissetrizes interiores
do triângulo ABC, o quociente QR/AR é
igual a
a) 0,3.
b) 0,45.
c) 0,35.
d) 0,5.
e) 0,4.
14) [UNICAMP] Na figura adiante, AB = AC
=
L
é o lado do decágono regular inscrito
em uma
circunferência de raio 1 e centro O.
a) Calcule o valor de
L.
b) Mostre que
15) FUVEST] Em um triângulo retângulo
OAB, retângulo em O, com OA = a e OB = b
são dados os pontos P em OA e Q em OB
de tal maneira que AP = PQ = QB = x.
Nestas condições, o valor de x é
a) √(ab) - a - b
b) a + b - √(2ab)
c) √(a² + b ²)
d) a + b + √(2ab)
e) √(ab) + a + b