Ângulos e relações métricas

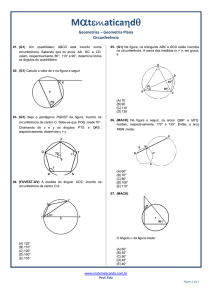
1. (Mack-SP) O quadrilátero ABCD da figura é inscritível. O valor de x é:
a) 36º
b) 48º
Resolução:
Em todo polígono inscrito os ângulos opostos
são suplementares: x+1280=1800 à x=520 .
c) 50º
d) 52º
e) 54º
2. (Cesgranrio-RJ) Em um círculo de centro 0, está inscrito o ângulo a. Se o arco
AMB mede 130º, o ângulo a mede:
a) 25º
Resolução:
b) 30º
c) 40º
α=
d) 45º
50 0
= 25 0
2
e) 50º
3. (UC-BA)
a) 10º
b) 15º
c) 20º
d) 25º
A medida do ângulo x, representado na figura é:
Resolução:
Supondo que 800 seja um ângulo
central. O ângulo inscrito
correspondente ao ângulo central
800 mede 400, pelo mesmo motivo
o ângulo x mede 200.
e) 30º
4. (UFES)
a) 50
b) 52
c) 54
d) 56
e) 58
5.
Na figura, a medida de a em graus é:
Resolução:
O arco de circunferência correspondente ao
ângulo de 320 mede 640. O outro ângulo
inscrito correspondente ao de 640 mede 320. A
soma dos ângulos internos de um triângulo
mede 1800 logo
α + 32 0 + 90 0 = 180 0 → α = 58 0 .
(Mark-SP)
AMB é igual a:
Na figura, sabe-se que m(CAD) = 20º e m(CED) = 70º. Então
a) 50º
b) 45º
c) 60º
d) 22º 30’
e) 30º
6. (Fuvest-SP) Os pontos A, B e C pertencem a uma circunferência de centro O.
Sabe-se que AO é perpendicular a OB e forma com BC um ângulo de 70º. Então, a
tangente à circunferência no ponto C forma com a reta AO um ângulo de:
a) 10º
b) 20º
c) 30º
d) 40º
e) 50º
7.
(Fatec-SP)
Na figura, os pontos A, B e C pertencem à circunferência de
centro O. Se β = 150º e γ = 50º, então a é igual a:
a) 15º
Resoluçao:
O ângulo beta é formado pelos lados
b) 20º
congruentes do triângulo isósceles AOB ( raio
c) 30º
e raio), assim, os ângulos da base desse
triângulo são 150 e 150. O ângulo B oposto
d) 35º
pelo vértice de gama se divide em
e) 45º
150+350=500. Estamos vendo que o triângulo
BOC é isósceles, com o ângulo alfa igual 350.
8. (Mack-SP)
medida de BD é:
a) 45º
b) 50º
c) 60º
d) 75º
e) 90º
Na figura, o ângulo AEC mede 80º e o arco AC mede 100º. A
Resolução:
AC + BD
,
2
AC+BD=1600, BD=1600-AC, BD=1600-1000
à BD=600.
Na figura estamos vendo 80 0 =
9. (UFES)
Na figura, os arcos AFB e CED medem 150º e 64º, respectivamente.
O ângulo APB mede em graus:
a) 100
Resolução:
b) 107
150 0 + 64 0
APB
=
= 107 0
c) 113
2
d) 121
e) 128
10. (FESP)
Os valores dos ângulos a, b e c são respectivamente:
Resolução:
a) 58º, 32º, 116º
Estamos vendo um triângulo
b) 32º, 58º, 64º
retângulo com os ângulos 900, 320
c) 58º, 32º, 64º
e x desconhecido: 900+320+x=1800
à x=580 à c=1160 à a=580 e
d) 32º, 58º, 116º
b=320.
e) 45º, 60º, 120º
11. (ITA-SP) Considere uma circunferência de centro em O e diâmetro AB. Tome
segmento BC tangente à circunferência, de modo que o ângulo BCA meça 30º. Seja
D o ponto de encontro da circunferência com o segmento AC e DE o segmento
paralelo a AB, com extremidades sobre a circunferência. A medida do segmento
DE será igual a:
a) metade da medida de AB
b) um terço da medida de AB
c) metade da medida de DC
d) dois terços da medida de AB
e) metade da medida de AE
12. (Vunesp-SP) Sejam A, B, C pontos distintos no interior de um círculo, sendo C o
centro do mesmo. Se construirmos um triângulo, inscrito no círculo, com um lado
passando por A, outro por B e outro por C, podemos afirmar que este triângulo:
a) é acutângulo
b) é retângulo
c) é obtusângulo
d) não é isósceles
e) pode ser eqüilátero
13. (UFES)
Inscreve-se um triângulo numa semi-circunferência cujo diâmetro
coincide com um dos lados do triângulo. Os outros lados do triângulo medem 5 cm
e 12 cm. O raio da semi-circunferência mede:
a) 5 cm
b) 6,5 cm
Resolução:
Todo triângulo inscrito numa semi-circunferência é retângulo e
pelo teorema de Pitágoras: d2=52+122 à d=13 à raio=6,5 cm.
c) 7,5 cm
d) 13 cm
e) 15 cm
14. (Fuvest-SP)
a) 0,6
O valor de x na figura é:
Resolução:
10.x=2.3 à x=0,6
b) 1
c) 4
d) 5
e) 20/3
15. (UEFS-BA)
Na figura, são dados
comprimento de AC, em cm, é:
a) 10
b) 12
c) 16
AE 1
= , BE = 8 cm e ED = 6 cm. O
EC 3
Resolução:
1
CE.EA=BE.ED à CE. .CE = 8.6 à
3
CE=12 e AC=12+4=16.
d) 18
e) 20
16. (EPCAR)
De um ponto P, traça-se uma tangente e uma secante a um círculo. Se
o segmento PT da tangente mede 8 m e o segmento PB da secante mede 16 cm, qual
deve ser, em m2, a área do círculo, se a secante contém o diâmetro do mesmo ?
a) 12 π
b) 18 π
c) 24 π
Resolução:
82=16.(16-2r) à r=6
A área do círculo:
A = π .6 2 = 36.π m 2
d) 30 π
e) 36 π
17. (Mack-SP)
11
a)
7
b)
24
7
Na figura, AB = 7 m, AD = 6 m e DE = 4 m. Então, BC é igual a:
Resolução:
AD.AE=AB.AC à 6.10=7.(7+BC) à
BC=11/7.
c) 5 m
d) 12 m
e) 11 m
18. (PUC-SP)
Na circunferência da figura de centro O e raio igual a 9 m, sabe-se
que a tangente PB = 2PA. A distância do ponto P à circunferência é:
a) 3 m
Resolução:
AP=?
b) 6 m
PB2=PA.PC à
c) 12 m
(2.PA)2=PA.(PA+9+9) à que
resolvendo encontramos PA=6
d) 18 m
m.
e) 24 m
19. ?