Uma proposta didática

Uma proposta didática
Ernesto Rosa
Os limites devem ser trabalhados duas vezes, uma antes e outra depois das
derivadas. A primeira vez é apenas olhando gráficos, intuitivamente, como ocorreu
historicamente. Na segunda vez, os épsilons e deltas. Desse modo obtemos melhor
rendimento didático, isto significa melhor aproveitamento de conteúdo e de
compreensão, com menor aversão.
Começamos com alguns exemplos que não precisam vir todos juntos, mas
entremeados com outros assuntos, preparando o que virá.
01. Para que valor tende o perímetro de um
polígono inscrito em uma circunferência de raio r,
quando o seu número n de lados cresce sem
parar? E a área?
02. Para que valor tende o raio r da
circunferência inscrita no triângulo retângulo onde
um cateto mede 6cm e o outro vai para 8cm? E
se x cresce além de qualquer número?
6
x
03. O êmbolo da seringa vai sendo
pressionado para dentro, fazendo que volume
tenda para zero. Para que valor tende a pressão
do ar dentro da seringa?
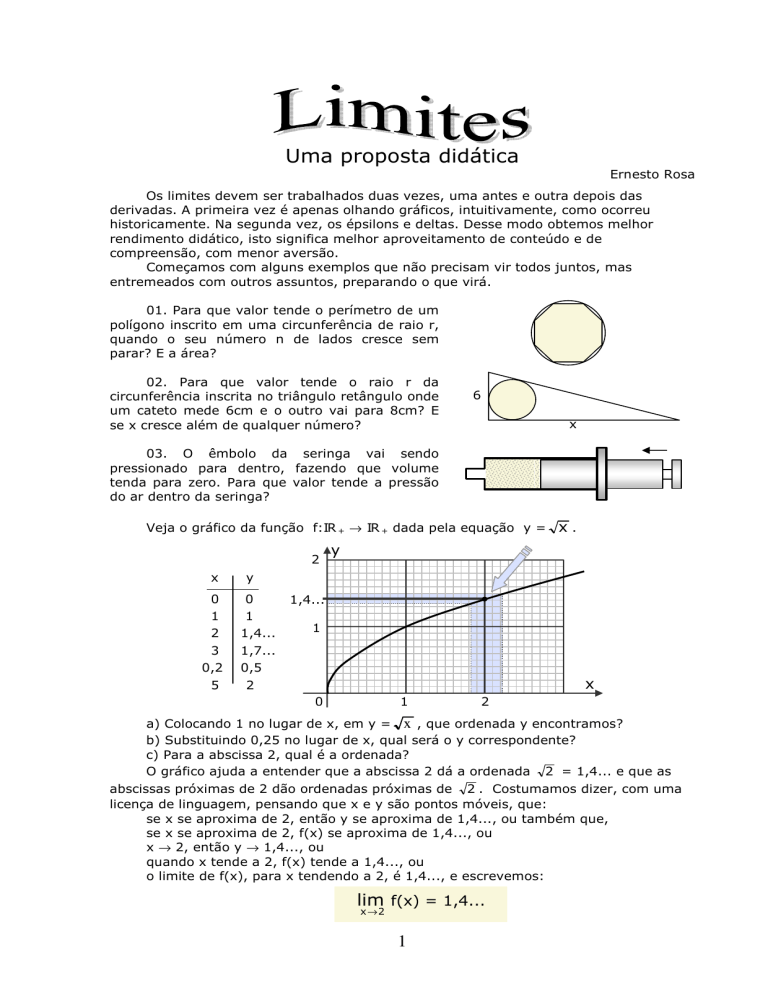
Veja o gráfico da função f:IR + → IR + dada pela equação y =
2
x
0
1
2
3
0,2
5
x.
y
y
0
1
1,4...
1,7...
0,5
2
1,4...
1
x
0
1
2
a) Colocando 1 no lugar de x, em y = x , que ordenada y encontramos?
b) Substituindo 0,25 no lugar de x, qual será o y correspondente?
c) Para a abscissa 2, qual é a ordenada?
O gráfico ajuda a entender que a abscissa 2 dá a ordenada 2 = 1,4... e que as
abscissas próximas de 2 dão ordenadas próximas de 2 . Costumamos dizer, com uma
licença de linguagem, pensando que x e y são pontos móveis, que:
se x se aproxima de 2, então y se aproxima de 1,4..., ou também que,
se x se aproxima de 2, f(x) se aproxima de 1,4..., ou
x → 2, então y → 1,4..., ou
quando x tende a 2, f(x) tende a 1,4..., ou
o limite de f(x), para x tendendo a 2, é 1,4..., e escrevemos:
lim f(x) = 1,4...
x→2
1
Portanto, no exemplo dado,
lim f ( x ) = lim x =
2 = 1,4...
x →2
x→2
O primeiro e mais geral método para cálculo de limites é EXAMINAR O GRÁFICO. Se
f(x) é função de x e x → a, olhe no gráfico para encontrar para onde tende f(x). Só que,
no gráfico é aproximado!
x e dê os valores aproximados dos limites:
c) lim
d) lim
x ~
x~
04. Examine o gráfico de y =
a) lim
b) lim x ~
x~
x →3
x →1,7
x → 0 ,4
x →1,2
Muitas vezes, podemos resolver algebricamente, simplesmente substituindo o x por
a. Isso pode ser feito nos pontos onde o gráfico é um “traço contínuo nas proximidades”
de f(a), ou seja, x → a acarreta que f(x) → f(a) e, além disso, se x chega ao a, f(x)
chega ao f(a). Esse é um segundo método de cálculo de limites. Veja os exemplos (faça
os gráficos, pelo menos nas proximidades do ponto estudado):
lim (x3 − 5x + 6) = 33 − 5⋅3 + 6 = 27 − 15 + 6 = 18
x →3
lim 3⋅cos x = 3⋅cos π = 3⋅(−1) = −3
x→π
lim
x→4
2
2
2 x − 3x = 2 4 − 3⋅ 4 = 2 4 = 16
05. Continue substituindo o x, para encontrar os limites:
a) lim (3x2 + 4) =
b) lim (x2 − 5x + 6) =
x →5
d)
lim
c)
x→3
2x +1
x −3
=
e)
2
i) lim x −25 =
x −5
x →5
sen x =
lim
lim 2x =
x → −1
x → π/6
x→4
Neste último caso deu zero sobre zero, que não é número, então podemos fatorar e
“cortar o fator anulante”, para recair no segundo método da substituição. Veja como:
2
(x +5)(x −5)
i) lim x −25 = lim
= lim (x + 5) = 5 + 5 = 10
x −5
x −5
x →5
x →5
x →5
Era o x−5 que estava anulando o numerador e o denominador quando o x era
trocado por 5.
06. Fatorar e “cortar o fator anulante” para calcular os limites:
a) lim
x→3
x −3
x2 −9
b)
lim
x→ −6
x 2 + 3 x − 18
x+6
x→3
Vamos compreender como “cortamos o fator anulante”.
Veja os dois gráficos das funções f e g dadas por:
2
(x −5)(x −2)
f(x) = x −7x +10 =
e
x −5
x −5
y
g(x) = x − 2
y
g
f
3
0
x − 3
=
x −3
c) lim
=
5
3
x
0
5
x
Os dois gráficos são “quase” iguais, f(x) = g(x) para qualquer número, exceto o 5.
Nos dois, quando x tende para 5, o y tende para 3. Só que, g(x) chega ao 3, enquanto
que não existe f(5). As duas ordenadas tendem para o mesmo ponto 3, mas somente
x 2 −7x +10 = lim (x − 2), apesar de f(5) não ser igual à g(5). Os
x −5
x→5
x→5
limites são iguais, não os valores das funções. Como queremos o limite e não o ponto,
então “cortamos o fator anulante”, trocando a primeira equação pela segunda, recaindo
g(x) chega lá. lim
2
no segundo método, somente para esse cálculo.
Um terceiro método é usar limites conhecidos, chamados limites fundamentais.
4
07. Confira o gráfico obtido com a expressão f(x) =
.
(x + 2)(x −1)2
y
x
-2
0
x
1
y
0
2
5
0,4
−1
−3
Os números 1 e −2 não servem para encontrar ordenadas. Portanto o domínio de f
é D = IR −{1, −2}
a) Abscissas muito grandes dão ordenadas positivas e próximas de 0.
b) Abscissas próximas de 2 fornecem ordenadas perto de 1.
c) Abscissas próximas de 1, sem chegarem ao 1, dão ordenadas muito grandes.
d) Abscissas próximas de 0 dão ordenadas próximas de 2.
e) Abscissas próximas de −1 dão ordenadas perto de 1.
f ) Abscissas próximas de −2, mas do lado direito de −2, dão ordenadas grandes
positivas.
g) Abscissas perto de −2, mas do lado esquerdo de −2, dão ordenadas “grandes”
negativas.
h) Com abscissas próximas de −3, obtemos ordenadas próximas de −1/4.
i) Com abscissas negativas de módulo grande, obtemos ordenadas negativas e
próximas de 0.
Parece-me que, nesse ponto, o aluno começa a compreender a difícil ideia de
dependência entre as variáveis, portanto passa a compreender um gráfico.
y
Veja o primeiro limite fundamental.
Se x cresce, 1/x vai para zero. A mesma
coisa ocorre em uma seringa ideal:
volume×pressão, com o volume crescendo.
lim 1 = 0
x→ ∞ x
0
x
Como conseqüência, temos os limites de funções racionais.
FUNÇÕES RACIONAIS
f(x) =
P(x)
Q(x)
08. Lembrando que 1/x vai para zero, quando x vai para infinito, calcular:
6 − 92
2
6
x
−
9
x
a) lim
= lim
x→ ∞ 2 − 6 + 8
x→ ∞ 2 x 2 − 6 x + 8
2
x
2x3 + x + 2
b) lim
= lim
x→ ∞
x→ ∞ 5x2 + 3
2x +
=
6 −0 = 6 = 3
2−0+0
2
x
1
x
5+
+
2
x2
3
x2
4x3 − 9
=
x→ ∞ 5x 6 − 6 x + 8
c) lim
3
=
Em a) o maior expoente do numerador é igual ao maior do denominador e, com x→
∞, a fração algébrica vai para 6/2 = 3
Em b) o maior expoente do numerador é maior que o maior do denominador e,
com x→ ∞, “sobra” x no numerador e o limite é infinito.
Em c) "sobra x no denominador" e a fração vai para zero.
Mais dois limites fundamentais importantes.
09. Pegue uma calculadora e faça os seguintes gráficos:
sen x
a) y =
,
b) y = (1 + 1 ) x ,
x
x
com x em radianos, tendendo a zero.
com x tendendo a infinito.
x
1
x
y
e
2
1
0
0,5
0
1
lim
x→0
sen x
=1
x
2
0,1
10
lim
x→ ∞
0,01
0,001
(1 + 1 ) x = e
x
e = 2,718281...
1
2
5
10
15
100
1000
Ver o artigo “O número e” na RPM nº 68 ou no site www.matinterativa.com.br.
Esses limites intuitivos acabam sendo um fechamento do estudo de gráficos.
Com esse roteiro e mais exercícios de treinamento, podemos entrar em técnicas de
derivação e suas aplicações. Depois, voltar a limites para formalizar e poder fazer as
demonstrações.
Ver o site:
www.matinterativa.com.br
4
y