Análise Matemática
Módulo 1
Sequências numéricas: definição e exemplos.
Revisão de cálculo de limite quando a variável tende para infinito
1. Sequência numéricas.
Uma sequência de números reais é uma lista infinita e ordenada, por exemplo
1
1
1
1
1; 3; 5; 7; 9;... ( 2n – 1) ... ou
;
;
...
...
ln 2 ln 4 ln 8 ln 2 n
Cada termo de uma sequência é indicado por an e n é referente ao índice indicativo
da posição que o terno na ocupa na sequência, por exemplo:
1
1 1 1
a n , temos a sequência 1; ; ; ;....
n
2 3 4
Exemplo 1 – módulo 1 – Análise Matemática
1
.
n
Solução: Para determinarmos os termos de uma série basta atribuímos valores
discretos corresponde a posição do termo: n = 1 (para o 1º termo que é indicado por
a1); n = 2 (para o 2º termo que é indicado por a2) e assim por diante.
Escreva os 5 primeiros termos da sequência a n 1
n=1
1
a1 1 2
1
n=3
a1 1
n=5
1
3
1
a1 1
5
4
3
6
5
n=2
a1 1
1 3
2 2
n=4
a1 1
1 5
4 4
Assim temos a sequência a n 1
1 3 4 5 6
2; ; ; ; ....
n 2 3 4 5
Exemplo 2 – módulo 1 – Análise Matemática
A soma dos n primeiros termos de uma sequência tem sua soma dada por
S(n) = n² para n 1e n indica aposição do termo. Determine os 4 primeiros termos
desta sequência.
Solução: observe que a expressão fornece a soma dos termos:
S(1) = a1 soma do 1º termo;
S(1) = 1² = 1 logo a1 = 1
S(2) = a1 + a2 soma dos 2 primeiros termos ou seja 1º + 2º termo;
S(2) = 2² = 4 a1 + a2 = 4 1 + a2 = 4 logo a2 = 3
S(3) = a1 + a2 + a3 soma dos 3 primeiros termos ou seja 1º + 2º +3ºtermo;
S(3) = 3² = 9 a1 + a2 + a3 = 9 1 + 3 + a3 = 9 logo a3 = 5
S(4) = a1 + a2 + a3+ a4
S(4) = 4² = 16 a1 + a2 + a3 + a4 = 16 1 + 3 + 5 + a4 = 16 logo a4 = 7
Assim temos a sequência {1; 3; 5; 7; ......}
Análise Matemática – módulo 1 -Pag.1
2. Revisão de cálculo de limite quando a variável tende para infinito
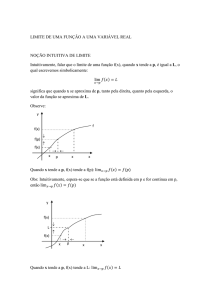
Limite de uma função é o valor para o qual se aproxima a função quando o valor de
seu domínio aproxima uma um determinado valor.
lim f ( X ) limite de f(x) quando x tende para a.
Notação: x a
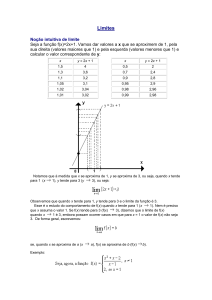
Como exemplo vamos analisar a função f ( x )
2x 1
quando o valor de x tende
x 1
para infinito () temos:
x
2
3
4
5
100
1000
10000
f(x)
5
3,5
3
2,75
2,03030 2,00300
2,0003
Pela seguência observamos que quando x tende para infinito o valor da função
tende para 2 então podemos fazer a representação:
lim
2x 1
2
x 1
x
Uma regra prática para calculo de limite quando x tende para infinito de funções do
p ( x)
tipo f ( x)
e considerarmos apenas os termos de maior grau do numerador e
q ( x)
denominador. No exemplo acima temos:
2x 1
2x
2
lim
lim 2
x x 1
x x
x 1
lim
O limite para infinito é usado no cálculo do n-éssimo termo (termo quando n tende
para infinito) de um sequência.
Exemplo 3 – módulo 1 – Análise Matemática
Calcule o n-éssimo termo da sequência definida por a n
Solução: Devemos calcular
2n ² 1
n 1
2n ² 1
n n 1
lim an lim
n
Este limite depende apenas dos termos de maior grau do numerador (2n²) e termo
de maior grau do denominador (n)
2n ² 1
2n ²
2n
lim
lim
n n 1
n n
n 1
lim an lim
n
agora basta fazer a substituição de
n por infinito().
2n 2.
n 1
1
lim
O n-éssimo termo desta seguência tende para infinito ou lim
n
Análise Matemática – módulo 1 -Pag.2
2n ² 1
n n 1
an lim
Exercícios propostos
1) Escreva os 6 primeiros termos da sequência definida por a n
2n ² 1
n 1
2) Escreva os 5 primeiros termos da sequência definida por a n
n 1
2n ² 1
3) Calcule o n-éssimo termo da sequência definida por a n
n 1
2n ² 1
4) Determine os 5 primeiros e último termo da sequência de termo geral a n
Análise Matemática – módulo 1 -Pag.3
3
.
2n ²