1
Teoria dos Circuitos e Fundamentos de Electrónica
Análise de Circuitos em
Regime Forçado Sinusoidal
Teresa Mendes de Almeida
[email protected]
DEEC
Área Científica de Electrónica
© T.M.Almeida
ACElectrónica
IST-DEECAbril de 2008
2
Matéria
Grandezas sinusoidais
características
posição relativa
diagrama temporal
amplitude complexa
diagrama vectorial
aplicação aos componentes
gerador de tensão e corrente
resistência
bobine
condensador
Impedância e Admitância
© T.M.Almeida
IST-DEEC-ACElectrónica
Generalização de Leis e
Teoremas
Regime forçado sinusoidal
Representação complexa
Potência Média
Resposta em frequência
Filtros passivos
Lei de Ohm, KVL, KCL
Divisores de tensão e corrente
Teorema da Sobreposição
Eq. Thévenin e Norton
Método dos Nós
Associação de impedâncias
passa-baixo e passa-alto
passa-banda e rejeita-banda
Exemplos de aplicação
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
3
Grandeza sinusoidal
Sinal sinusoidal (tensão ou corrente)
caracterizado por 3 parâmetros
amplitude → XM
[V] ou [A]
frequência
ω = 2π f
[rad / s]
[Hz]
fase na origem dos tempos → θ [rad]
Gráfico temporal
angular → ω
linear → f
representação gráfica em função do tempo
escala horizontal
tempo → t
[s]
fase → ωt
[rad]
Notação (encontrada nos livros)
π
π
i ( t ) = 7 cos (10t + 45º ) → i ( t ) = 7 cos 10t + 45º
= 7 cos 10t + = 7 cos (10t + 0, 785 )
180º
4
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
4
Desfasagem
Desfasagem (posição relativa entre 2 sinais)
2 sinais com mesma frequência e escritos da mesma forma (sin() ou cos())
x1 ( t ) = X M 1 cos (ωt + θ1 )
x2 ( t ) = X M 2 cos (ωt + θ 2 )
x1(t) está em avanço relativamente a x2 (t):
x2(t) está em avanço relativamente a x1 (t):
π
x2 ( t ) = cos ωt +
4
x1 ( t ) = cos (ωt )
∆θ12 = θ1-θ2
∆θ 21 = θ2-θ1
x1(t) está em avanço -45º
x2(t) está em avanço +45º
⇔ x1(t) está em atraso +45º
⇔ x2(t) está em atraso -45º
Sinais em
© T.M.Almeida
fase:
∆θ12 = 0º
oposição de fase: ∆θ12 = ± 180º
IST-DEEC-ACElectrónica
quadratura:
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
∆θ12 = ± 90º
Abril de 2008
5
Regime forçado sinusoidal
Num circuito linear, se sinal do gerador é sinusoidal, como
vão ser os sinais (tensões ou correntes) no circuito?
vai existir transitório quando gerador é ligado
extingue-se passado pouco tempo
permanece apenas influência do sinal sinusoidal
i (t ) = ?
v ( t ) = VM cos(ωt + θ v )
Se i(t) for a corrente numa resistência, bobine ou num condensador, como é a sua forma de onda?
vR ( t ) = R × iR ( t )
Resistência
i ( t ) = I M cos (ωt + θ I )
di ( t )
→ sinusoidal
Bobine
vL ( t ) = L × L
Condensador
dt
© T.M.Almeida
IST-DEEC-ACElectrónica
iC ( t ) = C ×
→ mesma frequência
dvC ( t )
dt
IM = ?
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
θI = ?
Abril de 2008
6
Regime forçado sinusoidal
Como calcular a corrente i(t) do circuito?
KVL
Lei Ohm
relação entre vL(t) e iL(t)
−v ( t ) + R × i ( t ) + L
di ( t )
=0
dt
⇔
L
di ( t )
+ R × i ( t ) = VM cos (ωt )
dt
resolvendo a equação diferencial obtém-se a solução
i (t ) =
v ( t ) = VM cos (ωt )
VM
2
R + (ω L )
2
ωL
cos ωt − tan −1
R
[ A]
para analisar um circuito simples (só 1 malha!) é preciso resolver uma
equação diferencial?!...
comparar com a análise de circuito resistivo semelhante (2 resistências)...
Como analisar o circuito sem ser necessário resolver equações
diferenciais/integrais?
© T.M.Almeida
utilizar o conceito de amplitude complexa → resolver equações algébricas
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
7
Amplitude complexa (phasor)
Representação complexa correspondente a sinal sinusoidal
e jφ = cos (φ ) + j sin (φ )
baseia-se na equação de Euler
x ( t ) = X M cos (ωt + θ )
para um sinal sinusoidal real
pode obter-se uma equivalência directa
XMe
j (ωt +θ )
= X M cos (ωt + θ ) + jX M sin (ωt + θ ) ⇒
1442443
j ωt +θ
x ( t ) = Re X M e ( )
x( t )
em regime forçado sinusoidal todos sinais têm mesma frequência (ω)
não se considera a informação da frequência
apenas se considera a informação da amplitude (XM) e da fase na
origem dos tempos (θ)
x ( t ) = X M cos (ωt + θ )
© T.M.Almeida
↔
X = X M e jθ = X M ∠θ = X M cos (θ ) + jX M sin (θ )
atenção à forma como é feita descrição do sinal no domínio do tempo!
cos( )
XM>0
e se estiver escrito de outra forma?
v ( t ) = 2sin ( 200t + π 3) → v ( t ) = 2 cos ( 200t + π 3 − π 2 ) = 2 cos ( 200t − π 6 )
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
8
Exemplos de aplicação
Determinar a frequência e a desfasagem entre as tensões
v1(t) = 12cos(377t-425º) V
v2(t) = 18sin(2513t+4,2º) V
Converter fasores para domínio do tempo
v1(t) = 12sin(100t+60º) V
v2(t) = -6cos(1000t+30º)
Determinar as amplitudes complexas V1 e V2
Abril de 2008
V1=10∠20º V
V2=12 ∠-60º V
Calcular fasores e desfasagem entre as várias correntes
© T.M.Almeida
i1(t)=2sin(377t+45º) A
i3(t)=-0,25sin(377t+60º) A
IST-DEEC-ACElectrónica
i2(t)=0,5cos(377t+10º) A
i4(t)=sin(377t) A
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
9
Analisar circuitos com amplitudes complexas
Analisar circuitos usando amplitudes complexas
transformar sinais do domínio do tempo para amplitudes complexas
analisar circuito resolvendo equações algébricas (com números complexos)
transformar amplitude complexa do resultado para o domínio do tempo
Gerador de Tensão
Gerador de Corrente
Resistência → generalização da Lei de Ohm
v ( t ) = VM cos (ωt + θ v )
IST-DEEC-ACElectrónica
i ( t ) = I M cos (ωt + θi ) ↔ I = I M ∠θi
θv = θi
i ( t ) = I M cos (ωt + θi )
© T.M.Almeida
v ( t ) = VM cos (ωt + θ v ) ↔ V = VM ∠θ v
R=
V = R× I
V VM j (θv −θi ) VM
e
=
=
IM
I IM
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
10
Analisar circuitos com amplitudes complexas
Propriedades
x ( t ) = X M cos (ωt + θ ) ↔
d
x (t ) ↔
dt
a1 x1 ( t ) + a2 x2 ( t ) ↔ a1 X 1 + a2 X 2
Bobine
tensão está em avanço
θv − θi = 90º
X = X M ∠θ
jω × X
V = jω L × I
Condensador
© T.M.Almeida
corrente está em avanço
IST-DEEC-ACElectrónica
θi − θ v = 90º
I = jωC × V
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
11
Exemplos de aplicação
A corrente numa resistência de 4Ω
Ω é I=12∠
∠60º A. Se a
frequência da corrente é 4kHz, como é a tensão aos terminais
da resistência, v(t)?
A corrente numa bobine (L=0,05H) é I=4 ∠-30º A. Se a
frequência da corrente é 50Hz, como é a tensão aos terminais
da bobine , v(t)?
Calcular a corrente na bobine (i(t) e I) quando a tensão aos
seus terminais é:
© T.M.Almeida
v1(t)=10cos(314t+45º) V
V2=-j5 V f=50Hz
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
12
Impedância e Admitância
Impedância – Z
quociente entre amplitudes complexas da tensão e da corrente
definida como anteriormente foi definida a resistência [Ω]
Z=
V
I
Z = R + jX
R – componente resistiva (resistência)
X – componente reactiva (reactância)
X>0 reactância do tipo indutivo
X<0 reactância do tipo capacitivo
X=0 → Z=R impedância é óhmica pura
R=0 → Z=jX impedância é reactiva pura
Z=
VM ∠θ v VM
=
∠ (θ v − θi )
I M ∠θi I M
Admitância – Y
© T.M.Almeida
inverso da impedância
G – condutância
B – susceptância
IST-DEEC-ACElectrónica
Y=
1
Z
Y = G + jB
G + jB =
1
R − jX
= 2
R + jX R + X 2
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
13
Generalização de Leis e Teoremas
Lei de Ohm pode ser generalizada
Resistência
Bobine
Condensador
ZR = R
ZL = jωL
ZC = 1/(jωC) = - j/(ωC)
V = Z×I
Generalização das Leis e Teoremas
leis e teoremas usados na análise de circuitos resistivos lineares com fontes
DC podem ser generalizados
Ie = I s
∑k Vk = 0
Leis de Kirchhoff (KCL e KVL)
e
s
Divisores de tensão e corrente
Método dos Nós
ZTh VTh = VOC
Equivalente de Thévenin
ZTh I N = I SC
Equivalente de Norton
Teorema da Sobreposição
…
∑
© T.M.Almeida
IST-DEEC-ACElectrónica
∑
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
14
Exemplo de aplicação
Como calcular a corrente i(t) do circuito?
v ( t ) = VM cos (ωt )
calcular a amplitude complexa do gerador de tensão
passar a informação para domínio da frequência
v ( t ) = VM cos (ωt ) → V = VM ∠0º = VM
KVL no sentido horário
−V + Z R I + Z L I = 0 ⇔ I =
⇔
VM
I=
R 2 + (ω L )
2
V
ZR + ZL
⇔
I=
VM
R + jω L
ωL
∠ − tan −1
R
passar resultado para o domínio do tempo
i (t ) =
© T.M.Almeida
I =?
VM
R 2 + (ω L )
IST-DEEC-ACElectrónica
2
ωL
cos ωt − tan −1
R
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
⇔
Resolução
de
equação algébrica
em vez de
equação diferencial
Abril de 2008
15
Associação de Impedâncias
Impedâncias associam-se como as resistências
Associação em série
impedâncias em série somam-se
Z S = Z1 + Z 2 + L + Z N
Associação em paralelo
1
1
1
1
= +
+L+
Z P Z1 Z 2
ZN
admitâncias em paralelo somam-se
YP = Y1 + Y2 + L + YN
Exemplos
f = 50 Hz
Z R = R = 25 Ω
Z L = jω L = 6, 28 Ω
1
= − j 63, 66 Ω
jωC
Z S = Z R + Z L + ZC
ZC =
Z S = 25 − j 57,38 Ω
© T.M.Almeida
IST-DEEC-ACElectrónica
Z eq = Z1 + Z 2 // ( Z 3 + Z 4 )
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
16
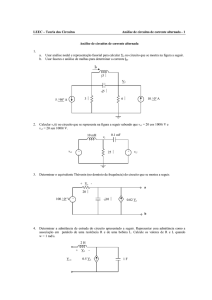
Exemplos de aplicação
Calcular a impedância/admitância equivalente
f=50Hz
f=400Hz
f=50Hz
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
17
Exemplos de aplicação
Calcular i(t), vR(t) e vC(t)
vs(t)=2cos(100t) V
Calcular quanto vale L para que
corrente esteja em fase com o sinal do
gerador de tensão
Calcular iC(t), iR(t) e vo(t)
f=50Hz IS=1A
Calcular i(t), iC(t) e vR(t)
Verificar KCL no nó superior
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
18
Potência Média
Potência instantânea
p (t ) = v (t ) × i (t ) =
1
V I
p ( t ) dt = M M cos (θ v − θi )
∫
TT
2
v ( t ) = VM cos (ωt + θ v )
dissipa energia
+
P=
VM I M
cos (θ v − θi )
2
P = Vef I ef cos (θ v − θ i )
Resistência
VM I M
cos (θ v − θi ) + cos ( 2ωt + θ v + θi )
2
Potência média (potência activa)
P=
i ( t ) = I M cos (ωt + θi )
θv = θi ⇒ PR =
I
V
−
V2
VM I M
= Vef I ef = R I ef2 = ef
2
R
Bobine ou Condensador
© T.M.Almeida
θ v − θi = ±90º
⇒
PC = PL = 0
potência média é nula
em parte do período armazena energia e no restante tempo liberta energia
não há dissipação de energia
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
Exemplos de aplicação
Calcular vo(t) e VO
Calcular
v(t) e V
Calcular vo(t)
Qual a potência dissipada
nas resistências?
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Variação da impedância com a frequência
19
Abril de 2008
20
Resistência – a impedância não varia com a frequência
ZR = R∠0º=R
Bobine e Condensador – a impedância varia com a frequência
ZL = jωL
ZL = ωL∠90º
ZC = 1/(jωC)
ZC = 1/(ωC) ∠-90º
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
21
Variação da impedância com a frequência
Como varia Zeq em função da frequência?
Z eq = Z R + Z L + Z C
1
Z eq = R + j ω L −
ωC
Z eq
1 − ω 2 LC
= R +
ωC
1
ωmin =
LC
2
2
1 − ω 2 LC
∠ ( Z eq ) = − tan
ω RC
−1
Os parâmetros do circuito reactivo variam com a frequência
do sinal sinusoidal do gerador
A resposta do circuito vai depender da frequência do sinal
É preciso estudar a resposta em frequência do circuito
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
22
Resposta em frequência
ZR
Vs
Z R + ( ZC + Z L )
Vo
ZR
=
Vs Z R + ( Z C + Z L )
Exemplo
Vo =
Escalas
logarítmicas
Vo
=
Vs
1
Vo
=
Vs
10-1
10-2
10-3
ω1
ω2
(rad/s)
1
1 − ω 2 LC
1+
ω RC
R
1
R + j ωL −
ωC
2
vs (t ) = 10 cos (ω1t + 0º ) V
vo (t ) = 10 cos (ω1t + 0º ) V
vs (t ) = 10 cos (ω2t + 0º ) V
V
∠ o
Vs
2
−1 1 − ω LC
=
tan
ω RC
π
vo (t ) = 7 cos ω2t − 50º
V
180º
ω1
© T.M.Almeida
IST-DEEC-ACElectrónica
ω2
(rad/s)
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
23
Filtros Passa-baixo e Passa-alto
Usar a dependência da frequência para filtrar sinais de
acordo com um determinado critério
Filtro passa-baixo
Filtro passa-alto
deixa passar sinais de baixa frequência
atenua (elimina) sinais de alta frequência
deixa passar sinais de alta frequência
atenua (elimina) sinais de baixa frequência
Medição do módulo em dB
dB
© T.M.Almeida
dB = deciBel
1/10 Bel
Vo
Vi
= 20 log
dB
0.01 0.1 1 2 1 2 1
−40 −20 −6
−3 0
2
3
Vo
Vi
ω0 – frequência de corte a -3dB
2 10 100
6 20 40
−3dB ⇔
1
≈ 0, 707
2
(½ potência)
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
24
Filtros Passa-baixo e Passa-alto
Filtro Passa-baixo
ZR = R
ZC =
1
jωC
-20dB/déc
τ = RC
Vo
ZC
1
1
=
=
=
V1 Z R + Z C 1 + jω RC 1 + jωτ
Filtro Passa-alto
+20dB/déc
Vo
ZR
jω RC
jωτ
=
=
=
V1 Z R + Z C 1 + jω RC 1 + jωτ
© T.M.Almeida
IST-DEEC-ACElectrónica
Vo
Vi
= 20 log
dB
Vo
Vi
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008
Filtros Passa-banda e Rejeita-banda
Filtro Passa-banda
deixa passar uma banda de frequências
ω0 – frequência central
ωLO, ωHI – limites da banda de passagem (ωHI -ωLO)
Vo
ZR
=
=
V1 Z R + ( Z L + Z C )
25
R
1
R + j ωL −
ωC
Filtro Rejeita-banda
rejeita uma banda de frequência (ωHI -ωLO)
Vo
Z L + ZC
=
V1 Z R + ( Z L + Z C )
© T.M.Almeida
IST-DEEC-ACElectrónica
1
j ωL −
ωC
=
1
R + j ωL −
ωC
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Exemplos de aplicação
Abril de 2008
26
Qual a impedância equivalente de Thévenin vista pelo gerador
de entrada?
Qual a resposta em frequência (módulo e fase)?
Qual o tipo de filtragem realizada pelo circuito?
Ajuda para simplificar os cálculos
© T.M.Almeida
quando circuitos são mais complexos
considerar variável s = jω → ZL=sL ZC=1/(sC)
fazer cálculos com variável s
no fim substituir s por jω
IST-DEEC-ACElectrónica
TCFE Análise de Circuitos em Regime Forçado Sinusoidal
Abril de 2008