Exercícios de aplicação 1 1. Prove no lançamento horizontal de um

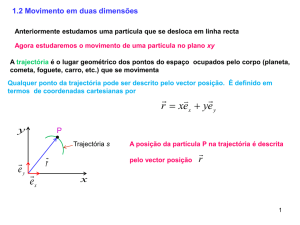
Exercícios de aplicação 1
1. Prove no lançamento horizontal de um projéctil a equação cartesiana da trajectória é:
g
y  2  x 2 e que representa uma parábola.
2v0
2. Demonstre as grandezas cinemáticas 5 e 6.
3. De uma altura de 15 m lança-se horizontalmente uma bola com velocidade de 20 m/s.

Considere || g || 10m / s 2 e despreze a resistência do ar.
3.1 Escreva as equações paramétricas do movimento da bola.
3.2 Quanto tempo demora a queda?
3.3 A que distancia do ponto de lançamento cai a bola?
3.4 Qual é a velocidade da bola imediatamente antes de atingir o solo?
Exercícios de aplicação 2
1. Demonstre que equação da trajectória é para o lançamento oblíquo para cima (quando x 0=0 e
y0=0) é:
y  tan   x 
g
 x2
2v  cos 2 
2
0
2. Com base na equação paramétrica do lançamento oblíquo para cima determine as seguintes
grandezas cinemáticas:
a)
Vector posição;
b)
Vector velocidade e os seus respectivos componentes;
c)
O módulo do vector velocidade;
d)
O vector aceleração
e)
As componentes norma e tangencial do vector aceleração.
3. Sabendo que na altura máxima v y  0 , demonstre que a expressão do tempo de subida e:
ts 
v0  sin 
g
4. Demonstre que se y0 =0, A altura máxima é:
y max 
v02  sin 2 
2g
5. Determine a expressão correspondente ao tempo que decorre entre o lançamento e a colisão
com projéctil com o solo (tempo do voo do projéctil)?
a) Quanto y0  0 ;
b) Quanto y0  0 ;
6. O alcance horizontal do projéctil, X, corresponde à abcissa no instante correspondente ao
tempo de voo do projéctil (tempo se subida mais o tempo de descida). Demonstre que se y0 =0,
o alcance horizontal é:
x
v02  sin 2
g
Dado: 2  sin   cos   sin 2
7. Qual é o valor do ângulo que implica o projéctil atingir um alcance máximo?
8. Pode-se fazer dois lançamentos oblíquos para cima, com velocidades de intensidades iguais,
segundo dois ângulos diferentes (  e  ) em que o projéctil atinge o mesmo alcance.


| v01 || v02 |
Determine  .
9. Uma bola de futebol é rematada com uma velocidade de 20 m/s segundo uma ângulo de 30º
com a horizontal. Considere g = 10m/s2 e despreze a resistência do ar.
9.1 Escreve a equação paramétrica do movimento.
9.2 Calcule a altura máxima atingida.
9.3 Qual o alcance horizontal da bola.
10. A figura representa o perfil de um terreno e um ponto O onde está instalado um canhão que
atira balas com a velocidade de 1,0 x 102 m/s. Calcule o maior comprimento BC que está livre
do bombardeiro. Dados: OA  960 m; AB  350 m .