amortecimento em dinâmica de estruturas

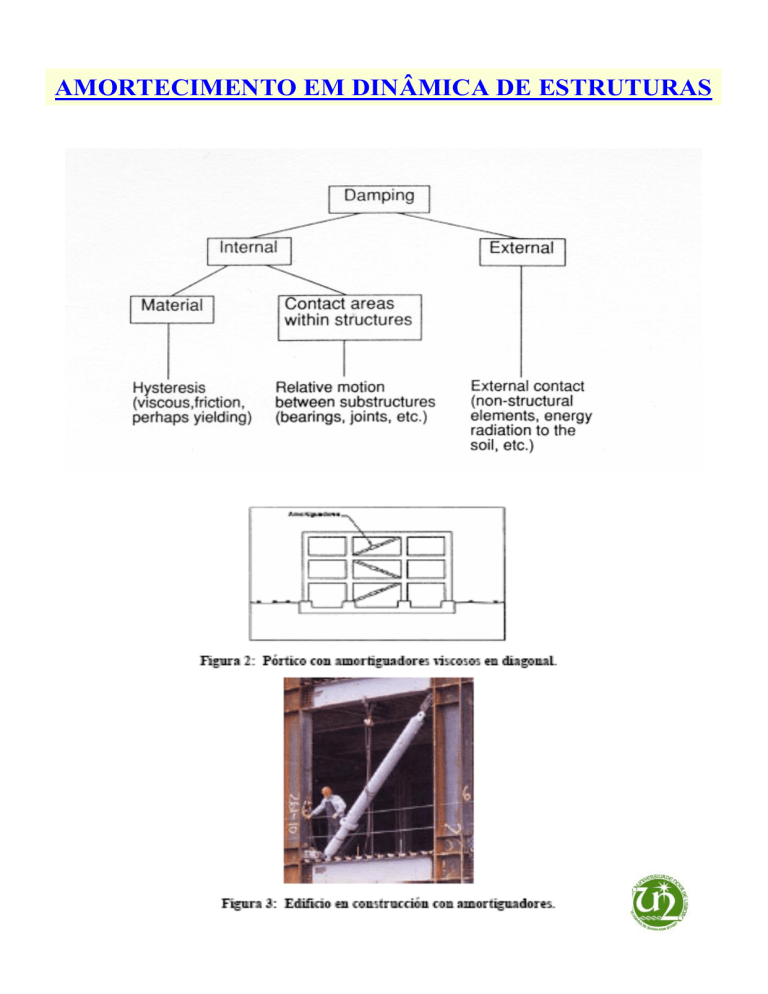
AMORTECIMENTO EM DINÂMICA DE ESTRUTURAS
Sistema típico
Amortecimento modelado como viscoso
Relembrando:
Amortecimento estrutural associa-se a:
. Tipo de material
. Estágio de deformação
ESTRUTURAS
- Betão Armado :e.g. de 5 a 9% de crítico
- Aço: de 2 a 5% de crítico
- Solos: maior complexidade
Amortecimento Viscoso
Modelo Kelvin- Voigt :
P = ku + cu&
. A força de amortecimento P depende da taxa de aplicação
da deformação, i.e. da velocidade de deformação (strain
rate)
. Quanto maior essa velocidade , maior a força P que causa
a mesma deformação u
Se P = P(u, du/dt ) for desenvolvida em série e aproximada
mantendo apenas termos lineares na velocidade tem-se a
expressão habitual que é suficientemente rigorosa nos casos
correntes de dinâmica de estruturas
Dissipação de Energia
http://ocw.mit.edu/NR/rdonlyres/Materials-Science-and-Engineering/3-11Mechanics-of-MaterialsFall1999
Ciclo de Histerese
Amortecimento Histerético
Será razoável, nesse caso, manter o modelo
P= c du/dt ?
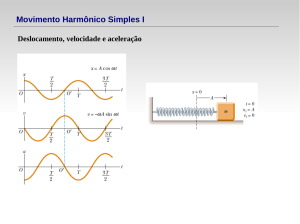
Se o movimento do oscilador for harmónico, em regime estacionário i.e.
pode escrever-se u = u0 sinωt
e obtem-se
P = k u0 sinωt + c ωu0 cosωt
u = u 0 sin ωt
⎧
⎨
⎩P / ku0 = sin ωt + [(ωc) / k ] cos ωt
http://mathworld.wolfram.com/Ellipse.html, mostra a equação de elipse
para Δ≠0, J>0 e Δ/L<0 , com
⎡a b d ⎤
⎡a b⎤
⎢
⎥
Δ= b c f ,J=⎢
,L=a+c
⎥
⎢
⎥
b c⎦
⎣
⎢⎣d f g ⎥⎦
Pode provar-se que
P = k u0 sinωt + c ωu0 cosωt
é equação de elipse que traduz a força reactiva em função de u,
para o caso de haver amortecimento viscoso.
Logo, pode usar-se
&& + cu& + ku = − Mu
&& g
Mu
para representar
&& + V (u& , u ) = − Mu
&& g
Mu
e representar os efeitos não lineares de histerese.
Amortecimento viscoso “equivalente” ao histerético
Energia Potencial Máxima
Energia dissipada por
ciclo no loop
Ue = 0.5 k u02
2π/ ω
ΔW = ∫ P(t)du = πcωu 02
0
Resulta:
⎧ ΔW 2πcω
=
1 ΔW
⎪
k
→β =
⎨ Ue
4π U e
⎪c = c β = 2β Mω
cr
⎩
Slide EERI
Hipótese: igual velocidade máxima dos dois sistemas
a)
Tmax=Vmax
0.5Mv 2max = 0.5ku 012 → u 01 =
k
v
M max
b)
Cria-se rótula na base porque a força resistente é inferior à
força elástica última
u02 = uy2 + upl
Segundo Sistema
. Ao esgotar energia cinética, em D, a força de
restituição V2 força o movimento no sentido inverso
. Energia dissipada quando V=0 é dada por área de OADG
. Energia potencial recuperada é dada por área de GDE
CONCLUSÃO:
A resistência à acção dinâmica pode conseguir-se através
de forças de restituição elásticas de grande manitude ou
através de forças menores e deformações plásticas se o
sistema as admitir
A capacidade de deformação plástica chama-se ductilidade.
O factor de ductilidade pode definir-se por δu/δy
Que factor m se deve impor para reduzir
os esforços por um factorR?
1 + R 1 + 1/ R
μ=
=
2
2R
2
2
2
Obs. Desenvolvendo em série (2x-1), na vizinhança
de x=1, obtem-se a aproximação de R=1/μ
Propriedade “Empírica”:
Devido ao amortecimento, os valores dos deslocamentos máximos,
elástico e elastoplástico, são muito semelhantes, para a mesma
acção sísmica (Penelis e Kappos, pg. 34)
Aceite esta propriedade, a partir da Figura abaixo, por
geometria, pode obter-se:
Vu 1
R2 =
=
Vel μ
SNUBBERS
Snubbers are used where dynamic restraint is
required, but the pipe has to be allowed to move
thermally.
In operation, normal thermal expansion of the pipework causes the piston rod
to extend or retractat a velocity less than the lock-up velocity. In this situation, t
he snubber is inactive and the devicehas minimal effect on the behaviour of the
pipework. In a dynamic situation, shock or vibration forces which cause the rate
of displacement of the piston to exceed the lock-up velocity will cause
the regulating valves to close and the snubber limits the velocity. The resistive
capacity of the unit transfers the force to the structure and reduces the possibility
of overstressing the pipe or associated equipment connections.
The function of the bleed grooves is to control the velocity after lock-up.
For prolonged thrust, the bleed grooves are eliminated and the unit becomes a
rigid strut during lock-up.