LIMITES E CONTINUIDADE

LIMITES E CONTINUIDADE
Marina Vargas R. P. Gonçalvesa
a Departamento
1
de Matemática, Universidade Federal do Paraná, [email protected],
http:// www.estruturas.ufpr.br
LIMITES LATERAIS
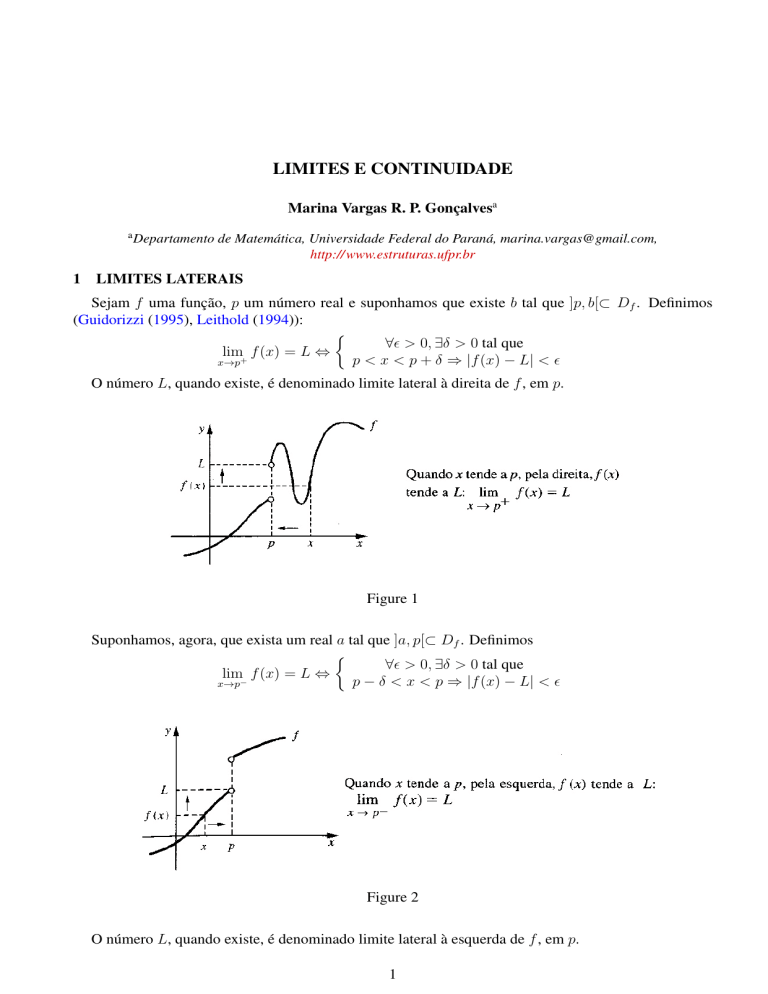
Sejam f uma função, p um número real e suponhamos que existe b tal que ]p, b[⊂ Df . Definimos
(Guidorizzi (1995), Leithold (1994)):
∀ > 0, ∃δ > 0 tal que
lim+ f (x) = L ⇔
p < x < p + δ ⇒ |f (x) − L| < x→p
O número L, quando existe, é denominado limite lateral à direita de f , em p.
Figure 1
Suponhamos, agora, que exista um real a tal que ]a, p[⊂ Df . Definimos
∀ > 0, ∃δ > 0 tal que
lim− f (x) = L ⇔
p − δ < x < p ⇒ |f (x) − L| < x→p
Figure 2
O número L, quando existe, é denominado limite lateral à esquerda de f , em p.
1
Teorema 1.1 lim f (x) ⇔ lim+ f (x) = lim− f (x)
x→p
x→p
x→p
Exemplo 1.1 Calcule lim+ f (x) e lim− f (x), sendo
x→1
x→1
2
x
se x < 1
f (x) =
2x se x > 1
Sol.:
lim+ f (x) = lim 2x = 2
x→1
x→1
lim− f (x) = lim x2 = 1
x→1
x→1
@ lim f (x), pois lim+ f (x) 6= lim− f (x)
x→1
x→1
Exemplo 1.2 Calcule lim+
x→0
x→1
|x|
|x|
e lim−
x x→0 x
Sol.: |x|
1 se x > 0
=
−1 se x < 0
x
|x|
= lim 1 = 1
lim
x→0
x→0+ x
|x|
lim
= lim −1 = −1
x→0
x→0− x
@ lim f (x), pois lim+ f (x) 6= lim− f (x)
x→0
x→0
x→0
Teorema 1.2 Teorema do Confronto
Sejam f , g e h funções e suponhamos que exista r > 0 tal que
f (x) ≤ g(x) ≤ h(x)
para 0 < |x − p| < r. Nestas condições, se
lim f (x) = L = lim h(x)
x→p
x→p
então
lim g(x)
x→p
Demonstração:
Por hipótese, lim f (x) = lim h(x) = L.
x→p
x→p
Dado > 0, existem δ1 > 0 e δ2 > 0 tais que
0 < |x − p| < δ1 ⇒ L − < f (x) < L + 0 < |x − p| < δ2 ⇒ L − < h(x) < L + Tomando-se δ = min{δ1 , δ2 , r}, tem-se:
0 < |x − p| < δ ⇒ L − < f (x) ≤ g(x) ≤ h(x) < L + logo
0 < |x − p| < δ ⇒ L − < g(x) < L + ou seja
lim g(x) = L.
x→p
2
LIMITES INFINITOS
Definição 2.1 Seja f uma função e suponhamos que existe a tal que ]a, +∞[⊂ Df . Definimos:
∀ > 0, ∃δ > 0, com δ > a tal que
lim f (x) = L ⇔
x > δ ⇒ |f (x) − L| < x→+∞
Figure 3
Definição 2.2 Seja f uma função e suponhamos que existe b tal que ] − ∞, b[⊂ Df . Definimos:
∀ > 0, ∃δ > 0, com − δ < b tal que
lim f (x) = L ⇔
x < −δ ⇒ |f (x) − L| < x→−∞
1
=
x→+∞ x
Exemplo 2.1 Calcule lim
Seja,
x
1
f (x) 1
assim,
2
1
2
10
1
10
100
1
100
1000
1
1000
→ +∞
→0
1
1
Dado > 0 e tomando δ = podemos escrever que x > δ ⇒ − < < x
e portanto
1
x>δ ⇒0−< <0+
x
x > δ ⇒ − < x−1 < 1
1
x>δ⇒− <x<
1
1
|x| < logo δ =
1
logo lim
=0
x→+∞ x
Figure 4
1
, onde n > 0
x→+∞ xn
Exemplo 2.2 Calcule lim
Sol.:
n
1
1
lim
= lim
x→+∞ xn
x→+∞
x
1
Seja = u, se x → +∞ então u → 0.
x
logo
1
lim n = lim un = 0
x→+∞ x
u→0
x5 + x4 + 1
=
x→∞ 2x5 + x + 1
Exemplo 2.3 Calcule lim
Sol.:
x5 1 + x1 + x15
1 + x1 + x15
1
x5 + x4 + 1
= lim
= lim 5 =
lim
1
1
1
1
5
x→∞ x 2 + 4 + 5
x→∞ 2x + x + 1
x→∞ 2 + 4 + 5
2
x
x
x
x
Definição 2.3 Suponhamos que existe a tal que ]a, +∞[⊂ Df . Definimos:
∀ > 0, ∃δ > 0, com δ > a tal que
lim f (x) = +∞ ⇔
x > δ ⇒ f (x) > x→+∞
lim f (x) = −∞ ⇔
x→+∞
∀ > 0, ∃δ > 0, com δ > a tal que
x > δ ⇒ f (x) < −
Definição 2.4 Seja f uma função, p um número real e suponhamos que existe b tal que ]p, b[⊂ Df .
Definimos:
∀ > 0, ∃δ > 0, com p + δ < b tal que
lim+ f (x) = +∞ ⇔
p < x < p + δ ⇒ f (x) > x→p
Figure 5
Exemplo 2.4 Calcule lim+
x→0
Seja,
x
1
f (x) 1
1
2
1
10
···
2 10
1
Assim, lim+ = +∞
x→0 x
1
=
x
1
1000
→ 0+
1000 → +∞
Figure 6
Teorema 2.1 Teorema do Valor Intermediário
Se f for contínua em [a, b] e se γ for um real compreendido entre f (a) e f (b), então existirá pelo
menos um c em [a, b] tal que f (c) = γ.
Figure 7
Teorema 2.2 Teorema do Anulamento ou de Bolzano
Se f for contínua no intervalo [a, b] e se f (a) e f (b) tiverem sinais contrários, então existirá pelo
menos um c em [a, b] tal que f (c) = 0.
Figure 8
Exemplo 2.5 Mostre que a equação x3 − 4x + 8 = 0 admite pelo menos uma raiz real.
Sol.:
Se f (0) = 8 e f (−3) = −7 e f é uma função contínua no intervalo [−3, 0], então existe pelo menos
um c em [−3, 0] tal que f (c) = 0, ou seja, f (x) admite pelo menos uma raiz entre [−3, 0].
Teorema 2.3 Teorema de Weierstrass
Se f for contínua em [a, b], então existirão x1 e x2 em [a, b] tais que f (x1 ) ≤ f (x) ≤ f (x2 ) para todo
x em [a, b].
Figure 9
O teorema de Weierstrass nos mostra que, se f for contínua em [a, b], então existirão x1 e x2 em [a, b]
tais que f (x1 ) é o valor mínimo de f em [a, b] e f (x2 ) o valor máximo de f em [a, b].
REFERENCES
Guidorizzi H.L. Um Curso de Cálculo, volume I. LTC, 1995.
Leithold L. O Cálculo com Geometria Analítica, volume I. Harbra, 1994.