Aula 28 - Derivadas das Funções Trigonométricas

1.1. Função seno
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
Chama-se função seno a
função definida de ℜ em ℜ por
f(x) = sen x.
Derivadas das Funções Trigonométricas
Inversas
Prof.: Rogério Dias Dalla Riva
4
Derivadas das Funções Trigonométricas
Inversas
1.1. Função seno
1.Funções trigonométricas
2.Funções circulares inversas
Para analisar o comportamento da função seno,
imagine que a extremidade P
de um arco, partindo da
origem, percorra a circunferência trigonométrica no sentido anti-horário.
3.Derivadas das funções trigonométricas inversas
4.Exemplos
5
1.1. Função seno
1. Funções trigonométricas
Nesse suposto deslocamento da extremidade do arco,
observamos que:
Vamos apresentar o comportamento das
funções seno, cosseno, tangente, cotangente,
secante e cossecante.
• De 0 a π/2 o seno cresce de
0 a 1.
• De π/2 a π o seno decresce
de 1 a 0.
• De π a 3π/2 o seno decresce
de 0 a -1.
• De 3π/2 a 2π o seno cresce
de -1 a 0.
3
6
1
1.1. Função seno
1.1. Função seno
Supondo que a extremidade P continue se deslocando
indefinidamente, a cada nova volta na circunferência
trigonométrica o seno assumirá, em idênticas condições,
todos os seus valores da primeira volta. Numa linguagem
simples, podemos dizer que a função f(x) = sen x repete-se
periodicamente de 2π em 2π.
7
1.1. Função seno
O menor valor (positivo) de T que satisfaz essa
igualdade é chamado período da função. O gráfico de sen(x)
é chamado senóide.
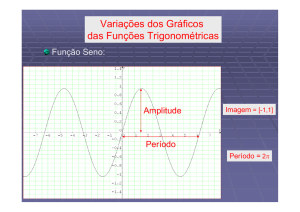
f ( x ) = sen x
⇒
D(f ) = ℝ

Im(f ) = [ −1; 1]
10
1.2. Função cosseno
Assim como analisamos
função seno, vamos analisar
comportamento de f(x)
cos(x) para x variando de 0
2π.
a
o
=
a
• De 0 a π/2 o cosseno decresce de 1 a 0.
• De π/2 a π o cosseno decresce de 0 a -1.
Na linguagem matemática escrevemos:
… = sen ( x − 4π ) = sen ( x − 2π ) = sen ( x ) = sen ( x + 2π ) = sen ( x + 4π ) = …
• De π a 3π/2 o cosseno cresce
de -1 a 0.
ou ainda
∀x ∈ ℝ e ∀k ∈ ℤ, sen x = sen ( x + k ⋅ 2π )
• De 3π/2 a 2π o cosseno
11
cresce de 0 a 1.
8
1.1. Função seno
1.2. Função cosseno
Da segunda volta em
diante, o cosseno passa a
repetir, em idênticas condições, os valores da primeira
volta. Isto é,
∀x ∈ ℝ e ∀k ∈ ℤ, cos x = cos ( x + k ⋅ 2π )
Então dizemos que: “A função f(x) = sen (x) é uma
função periódica de período igual a 2π”. De um modo geral,
uma função f é denominada periódica sempre que existe um
número T > 0, tal que, para todo x do domínio de f tem-se:
f (x) = f (x + T )
9
Então dizemos que a
função f(x) = cos (x) é uma
função periódica de período
igual a 2π.
12
2
1.2. Função cosseno
1.3. Função tangente
O gráfico da função cosseno é chamado cossenóide.
Note, na figura, que a cossenóide nada mais é do que a
senóide deslocada de π/2 unidades, na direção horizontal,
para a “esquerda”. Essa característica da cossenóide pode
13
ser traduzida assim:
1.2. Função cosseno
A função tangente também é periódica. Porém,
enquanto as funções seno e cosseno têm períodos iguais a
2π, a função tangente tem período igual a π.
16
1.3. Função tangente
π

∀x ∈ ℝ, cos x = sen  x + 
2

f ( x ) = cos x
⇒
D(f ) = ℝ

Im(f ) = [ −1; 1]
Isso significa que a cada meia-volta a função
tangente repete-se em idênticas condições. Isto é,
14
1.3. Função tangente
π


∀x ∈ ℝ e ∀k ∈ ℤ,  x ≠ + kπ  ⇒ tg x = tg ( x + kπ )
2


17
1.3. Função tangente
• De 0 a π/2 a tangente cresce de 0 a +∞.
Chama-se função tangente a função definida por
f ( x ) = tg x,
x≠
π
2
• De π/2 a π a tangente cresce de -∞ a 0.
+ kπ , k ∈ ℤ
15
18
3
1.3. Função tangente
1.4. Funções cotangente, secante e cossecante
P=π
Daí em diante, a cada meia-volta, a tangente
comporta-se exatamente como na primeira meia-volta.
f ( x ) = cotg x
D(f ) = { x ∈ ℝ / x ≠ kπ }

Im(f ) = ℝ
⇒
19
1.3. Função tangente
(k ∈ ℤ )
22
1.4. Funções cotangente, secante e cossecante
P = 2π
f ( x ) = tg x
⇒

π


D(f ) =  x ∈ ℝ / x ≠ + kπ 
2




Im(f ) = ℝ
(k ∈ ℤ )
20
f ( x ) = sec x
⇒

π


D(f ) =  x ∈ ℝ / x ≠ 2 + kπ 



Im(f ) = {y ∈ ℝ / y ≤ −1 ou

(k ∈ ℤ )
y ≥ 1}
23
1.4. Funções cotangente, secante e cossecante
1.4. Funções cotangente, secante e cossecante
Por serem menos importantes que as demais
funções trigonométricas, serão apresentadas de
forma resumida, enfatizando-se o domínio e o
conjunto-imagem das funções cotangente, secante
e cossecante.
P = 2π
21
f ( x ) = cossec x
⇒
D(f ) = {x ∈ ℝ / x ≠ k π } (k ∈ ℤ )

Im(f ) = {y ∈ ℝ / y ≤ −1 ou y ≥ 1}
24
4
2. Funções circulares inversas
7.1. Função arco-seno
As funções trigonométricas inversas são
também conhecidas como funções arco. Nessa
notação:
sen-1 x = arc sen x
cos-1 x = arc cos x
tg-1
cotg-1 x = arc cotg x
x = arc tg x
sec-1 x = arc sec x
Definição:
 π π
Para x ∈ [ −1; 1] e y ∈  − ;  , a função arco 2 2
seno é definida pela sentença
y = arc sen x ⇔ sen y = x
cossec-1 x = arc cossec x
25
7.1. Função arco-seno
28
7.1. Função arco-seno
A função de domínio ℜ definida por
f(x) = sen x não admite função inversa por não ser
injetora(*).
Veja estes exemplos:
π
1
a)
b) -
6
π
2
= arc sen
2
π  1
, pois sen   =
6 2
 π
= arc sen(−1), pois sen  −  = −1
 2
Este esquema mostra que a função arcoseno é a inversa da função seno:
Nota: Uma função f é chamada injetora se cada elemento de seu conjunto26
imagem é imagem de um único elemento do domínio.
29
7.1. Função arco-seno
7.1. Função arco-seno
Porém, restringindo o domínio da função
seno ao intervalo [- π/2, π/2] é possível definir sua
inversa, que é chamada função arco-seno e é
denotada pelo símbolo arc sen.
Gráfico de f(x) = arc sen x
Por exemplo, a sentença
π
6
significa:
π
6
= arc sen
1
2
é o arco cujo seno é igual a
1
2
27
30
5
2.1. Função arco-seno
7.2. Função arco-cosseno
Se considerarmos a função seno restrita ao
intervalo [-π/2, π/2] e com contradomínio [-1, 1],
isto é,
g: [-π/2, π/2] → [-1, 1]
A inversa da função cosseno é chamada
função arco-cosseno e é denotada por arc cos.
Definição:
tal que g(x) = sen x, a função g admitirá inversa e
g-1 será denominada função arco-seno. Notemos
que g-1 tem domínio [-1, 1], contradomínio [-π/2,
π/2] e associa a cada x ∈ [-1, 1] um y ∈ [-π/2, π/2]
tal que y é um arco cujo seno é x (indica-se y = arc
sen x). Temos, portanto, que:
Para x ∈ [ −1; 1] e y ∈ [0; π ], a função arco-cosseno é definida pela sentença
y = arc cos x ⇔ cos y = x
y = arc sen x ⇔ sen y = x e -π/2 ≤ y ≤ π/2
31
2.1. Função arco-seno
34
7.2. Função arco-cosseno
Veja estes exemplos:
π
3
3
π 
, pois cos   =
2
6
b ) π = arc cos( −1), pois cos (π ) = −1
a)
6
= arc cos
2
Este esquema mostra que a função arcocosseno é a inversa da função cosseno:
32
7.2. Função arco-cosseno
35
7.2. Função arco-cosseno
A exemplo da função seno, a função cosseno
não admite inversa quando seu domínio é o
conjunto ℜ. Assim, para definir a inversa da
função cosseno, vamos restringir o seu domínio ao
intervalo [0; π].
33
Gráfico de f(x) = arc cos x
36
6
2.2. Função arco-cosseno
7.3. Função arco-tangente
Se considerarmos a função cosseno restrita
ao intervalo [0, π] e com contradomínio [-1, 1], isto
é,
g: [0, π] → [-1, 1]
A inversa da função tangente é chamada
função arco-tangente e é denotada por arc tg.
Definição:
tal que g(x) = cos x, a função g admitirá inversa e
g-1 será denominada função arco-cosseno. Notemos
que g-1 tem domínio [-1, 1], contradomínio [0, π] e
associa a cada x ∈ [-1, 1] um y ∈ [0, π] tal que y é
um arco cujo cosseno é x (indica-se y = arc cos x).
Temos, portanto, que:
π π
Para x ∈ ℝ e y ∈  − ;  , a função arco-tan 2 2
gente é definida por
y = arc tg x ⇔ tg y = x
y = arc cos x ⇔ cos y = x e 0 ≤ y ≤ π
37
40
7.3. Função arco-tangente
2.2. Função arco-cosseno
Observe estes exemplos:
a)
π
4
b) -
π
3
π 
= arc tg (1) , pois tg   = 1
4
 π
= arc tg( − 3), pois tg  −  = − 3
 3
41
38
7.3. Função arco-tangente
7.3. Função arco-tangente
Para definir o inverso da função tangente,
vamos restringir o inverso da mesma ao intervalo
(-π/2, π/2). Observe o gráfico seguinte e note que,
nesse intervalo, a função tangente é bijetora.
39
Gráfico de f(x) = arc tg x
42
7
2.3. Função arco-tangente
2.4. Quadro resumo
Função trigonométrica com
domínio modificado
Função trigonométrica
Se considerarmos a função tangente
restrita ao intervalo aberto (-π/2, π/2) e com
contradomínio ℜ, isto é,
g: (-π/2, π/2) → ℜ
tal que g(x) = tg x, a função g admitirá inversa e g-1
será denominada função arco-tangente. Notemos
que g-1 tem domínio ℜ, contradomínio (-π/2, π/2) e
associa a cada x ∈ ℜ um y ∈ (-π/2, π/2) tal que y é
um arco cuja tangente é x (indica-se y = arc tg x).
Temos, portanto, que:
y = arc tg x ⇔ tg y = x e -π/2 ≤ y ≤ π/2
43
Inversa trigonométrica
y = sen x
Domínio: (-∞, +∞)
Imagem: [-1, 1]
y = sen x
Domínio: [- π/2, π/2]
Imagem: [-1, 1]
y = sen-1 x = arc sen x
Domínio: [-1, 1]
Imagem: [- π/2, π/2]
y = cos x
Domínio: (-∞, +∞)
Imagem: [-1, 1]
y = cos x
Domínio: [0, π]
Imagem: [-1, 1]
y = cos-1 x = arc cos x
Domínio: [-1, 1]
Imagem: [0, π]
y = tg x
Domínio: {x ∈ ℜ/x ≠ π/2 + k π, k ∈ Z}
y = tg x
Domínio: (- π/2, π/2)
Imagem: (-∞, +∞)
y = tg-1 x = arc tg x
Domínio: (-∞, +∞)
Imagem: (- π/2, π/2)
y = cotg x
Domínio: (0, π)
Imagem: (-∞, +∞)
y = cotg-1 x = arc cotg x
Domínio: (-∞, +∞)
Imagem: (0, π)
y = sec x
Domínio: [-π, -π/2) U [0, π/2)
Imagem: (-∞, 1] U [1, + ∞)
y = sec-1 x = arc sec x
Domínio: (-∞, 1] U [1, + ∞)
Imagem: [-π, -π/2) U [0, π/2)
y = cossec x
Domínio: (-π, -π/2] U (0, π/2]
Imagem: (-∞, 1] U [1, + ∞)
y = cossec-1 x = arc cossec x
Domínio: (-∞, 1] U [1, + ∞)
46
Imagem: (-π, -π/2] U (0, π/2]
Imagem: (-∞, +∞)
y = cotg x
Domínio: {x ∈ ℜ/x ≠ k π, k ∈ Z}
Imagem: (-∞, +∞)
y = sec x
Domínio: {x ∈ ℜ/x ≠ π/2 + k π, k ∈ Z}
Imagem: (-∞, 1] U [1, + ∞)
y = cossec x
Domínio: {x ∈ ℜ/x ≠ k π, k ∈ Z}
Imagem: (-∞, 1] U [1, + ∞)
3. Derivadas das funções trigonométricas inversas
2.3. Função arco-tangente
Aqui, usaremos a diferenciação implícita
para determinar as derivadas das funções
trigonométricas inversas, supondo que essas
funções sejam diferenciáveis.
47
44
3.1. Derivada de arc sen x
2.4. Quadro resumo
Atenção! Nenhuma função trigonométrica
possui inversa, o que fazemos aqui é a modificação
do domínio destas funções, criando assim novas
funções que sejam inversíveis.
Lembre-se que a função inversa da função
seno é dada por sen-1 x = arc sen x.
y = sen-1 x significa sen y = x
e -π/2 ≤ y ≤ π/2
Diferenciando sen y = x implicitamente em
relação a x obtemos
cos y
dy
dy
1
=1 ⇒
=
dx
dx cos y
Agora cos y ≥ 0, uma vez que -π/2 ≤ y ≤ π/2,
logo:
cos y = 1 − sen2 y = 1 − x 2
45
48
8
3.1. Derivada de arc sen x
3.3. Derivada de arc tg x
Lembre-se que a função inversa da função
tangente é dada por tg-1 x = arc tg x.
dy
1
1
=
=
dx cos y
1− x 2
y = tg-1 x significa tg y = x
Portanto
(
e
-π/2 ≤ y ≤ π/2
Diferenciando tg y = x implicitamente em
relação a x obtemos
)
d
1
sen−1 x =
dx
1− x 2
sec 2 y
dy
dy
1
=1 ⇒
=
dx
dx sec 2 y
Da identidade sec2 y = 1 + tg2 y, temos
sec 2 y = 1 + tg2 y = 1 + x 2
49
3.2. Derivada de arc cos x
52
3.3. Derivada de arc tg x
Lembre-se que a função inversa da função
cosseno é dada por cos-1 x = arc cos x.
y = cos-1 x significa cos y = x
e 0≤y≤π
dy
1
1
=
=
dx sec 2 y 1 + x 2
Portanto
Diferenciando cos y = x implicitamente em
relação a x obtemos
(
)
d
1
tg−1 x =
dx
1+ x 2
dy
dy
1
−sen y
=1 ⇒
=−
dx
dx
sen y
Agora sen y > 0, uma vez que 0< y< π, logo:
sen y = 1 − cos2 y = 1 − x 2
50
3.2. Derivada de arc cos x
53
3.4. Derivada de arc cotg x
Lembre-se que a função inversa da função
cotangente é dada por cotg-1 x = arc cotg x.
dy
1
1
=−
=−
dx
sen y
1− x 2
y = cotg-1 x significa cotg y = x
Portanto
(
e
0≤y≤π
Diferenciando cotg y = x implicitamente em
relação a x obtemos
)
d
1
cos−1 x = −
dx
1− x2
−cossec 2 y
dy
dy
1
=1 ⇒
=−
dx
dx
cossec 2 y
Da identidade cossec2 y = 1 + cotg2 y, temos
cos sec 2 y = 1 + cotg 2 y = 1 + x 2
51
54
9
3.4. Derivada de arc cotg x
3.6. Derivada de arc cossec x
Lembre-se que a função inversa da função
cossecante é dada por cossec-1 x = arc cossec x.
dy
1
1
=−
=−
dx
cossec 2 y
1+ x 2
y = cossec-1 x
Portanto
(
significa
cossec y = x
e
{y ∈ ℜ/ (-π, -π/2] U (0, π/2]}
)
d
1
cotg−1 x = −
dx
1+ x 2
Diferenciando cossec y = x implicitamente
em relação a x obtemos
−cossec y cotg y
dy
dy
1
=1 ⇒
=−
dx
dx
cossec y cotg y
Da identidade cotg2 y = cossec2 y - 1, temos
cotg y = cossec 2 y − 1 = x 2 − 1
55
3.5. Derivada de arc sec x
58
3.6. Derivada de arc cossec x
Lembre-se que a função inversa da função
secante é dada por sec-1 x = arc sec x.
y = sec-1 x
significa
sec y = x
dy
1
1
=−
=−
dx
cossec y cotg y
x x2 − 1
e
Portanto
{y ∈ ℜ/ [- π, -π/2) U [0, π/2)}
(
sec y tg y
)
d
1
cossec −1 x = −
dx
x x2 − 1
Diferenciando sec y = x implicitamente em
relação a x obtemos
dy
dy
1
=1 ⇒
=
dx
dx sec y tg y
Da identidade tg2 y = sec2 y - 1, temos
tg y = sec 2 y − 1 = x 2 − 1
56
3.5. Derivada de arc sec x
59
3.7. Resumo
Se u for uma função de x, derivável,
dy
1
1
=
=
dx sec y tg y x x 2 − 1
(
(
)
d
1 du
sen−1 u =
dx
1 − u 2 dx
Portanto
)
d
1
sec −1 x =
dx
x x2 − 1
(
)
d
1 du
cos −1 u = −
dx
1 − u 2 dx
(
)
d
1 du
tg−1 u =
dx
1 + u 2 dx
57
(
)
d
1 du
cotg−1 u = −
dx
1 + u 2 dx
(
)
d
1
du
sec −1 u =
dx
u u 2 − 1 dx
(
)
d
1
du
cossec −1 u = −
dx
u u 2 − 1 dx
60
10
4. Exemplos
4. Exemplos
x
Exemplo 4: Ache dy/dx se ln ( x + y ) = tg−1  
y
Exemplo 1: Derive y = sen-1 x2.
(

)
d
1 du
sen−1 u =
dx
1 − u 2 dx
d
1
sen−1 x 2 =
2x
2
dx
1− x 2
(
)
(
)
1  dy 
⋅ 1+
=
x + y  dx 
( )
d
2x
sen−1 x 2 =
dx
1− x 4
dy
dy
1+
dx ⇒
dx =
x+y
y ⋅1− x ⋅
(
4. Exemplos

dy
dx
1
1
⋅
⋅
2
y2
x2
y2
x
1+ 2
1+  
y
y
dy
dy
dy
dy
2
y−x
1+
y−x
1+
1
dx
dx =
dx ⇒
dx = y
⋅
⋅
2
y 2 + x2
y 2 + x2
x+y
y2
x+y
y
y2
dy
dy
1+
y−x
dx =
dx ⇒ y 2 + x 2 + y 2 + x 2 ⋅ dy = xy + y 2 − x 2 + xy ⋅ dy
2
x+y
y + x2
dx
dx
dy
dy
dy
y 2 + x2 ⋅
+ x 2 + xy ⋅
= xy − x 2 ⇒ 2 x 2 + xy + y 2 ⋅
= xy − x 2
dx
dx
dx
x (y − x)
dy
xy − x 2
dy
=
⇒
=
dx 2 x 2 + xy + y 2
dx 2 x 2 + xy + y 2
(
61
y −x
)
(
)
)
(
(
)
)
64
4. Exemplos
Exemplo 2: Derive f ( x ) = tg−1
(
)
d
1 du
tg−1 u =
=
dx
1 + u 2 dx
1
 1 
1+ 

 x + 1
d  −1 1 
1
tg
=
dx 
x + 1  ( x + 1)2
1
+
2
2
( x + 1) ( x + 1)
d  −1
tg
dx 
2
Exemplo 5: Derive a função f ( x ) = sec −1 ( 3e x )
1
x +1

1 

⋅−
 ( x + 1)2 


3e x
x
f ' (x) =
2
−1
(
3e x
)
2
(
⋅ 3e x
1
3e x

1 
1
1 

=
⋅−
x + 1  x 2 + 2 x + 1 + 1  ( x + 1)2 


2
( x + 1)

1
=−

x 2 + 2x + 2

( 3e )
f ' (x) =

1 

⋅−
 ( x + 1)2 


2
( x + 1) 
d  −1 1 
1
tg
⋅ −
=
dx 
x + 1  x 2 + 2x + 2  ( x + 1)2

1
f ' (x) =
−1
(
)
⋅ 3e x
)
1
9e 2 x − 1
62
4. Exemplos
65
4. Exemplos
Exemplo 3: Derive y = x 3 cotg−1
dy
= 3 x 2 ⋅ cotg−1
dx
dy
= 3 x 2 ⋅ cotg−1
dx


x
1
+ x3 ⋅  −
2
3
 1+ x

9



x  x3  1
−
⋅
2
3  9+x  3


 9 
x
3
Exemplo 6: Derive a função f ( x ) = x cos sec −1

 1
⋅
 3


dy
x
9 x3 1
= 3 x 2 ⋅ cotg−1 −
⋅
dx
3 9 + x2 3
dy
x
3x 3
= 3 x 2 ⋅ cotg−1 −
dx
3 9 + x2
63
f ' ( x ) = cossec −1




1
1

 1 
+ x −
⋅  − 2 
2
x
x

 1  1  −1 
 x  x 



f ' ( x ) = cossec −1


1  −x2
 1
+
⋅ −
x  1 − x 2  x 2

x2

f ' ( x ) = cossec −1


1  1
+
2
x
 1− x
 x
f ' ( x ) = cossec −1
1  x 
+

x  1− x 2 
1
x













66
11
4. Exemplos
4. Exemplos
No exemplo a seguir, um observador está
olhando um quadro colocado em uma parede. Veja a
figura a seguir. Quando o observador está
afastado da parede, o ângulo segundo o qual ele vê
o quadro é pequeno. À medida que o observador se
aproxima da parede, o ângulo irá aumentando, até
atingir um valor máximo. Então, se o observador
continuar se aproximando, o ângulo diminuirá.
Quando o ângulo for máximo, diremos que o
observador tem a “melhor visão” do quadro.
Vemos, da figura, que:
cotg β =
x
x
e cotgα =
3
2
Como 0 < β <
π
2
e 0<α <
π
2
x
x
β = cotg−1
e α = cotg−1
3
2
Substituindo esses valores de α e β na
relação θ = β - α.
θ = cotg-1
x
x
− cotg-1
3
2
67
70
4. Exemplos
4. Exemplos
Derivando com relação a x, teremos:
Exemplo 7: Um quadro com 1 m de altura é
colocado em uma parede de tal forma que sua base
esteja 2 m acima do nível dos olhos de um
observador. Quantos metros o observador deverá
se afastar da parede, para obter a melhor visão do
quadro, isto é, para que o ângulo segundo o qual ele
vê o quadro seja o máximo?
dθ
=−
dx
1
1
3
2
3
2
+
=−
+
2
2
9 + x2 4 + x2
x
x
1 +   1+  
3
2
Equacionando
dθ
= 0 , iremos obter
dx
2(9 + x 2 ) − 3(4 + x 2 ) = 0
− x 2 + (18 − 12) = 0
x2 = 6
x ≅ 2,45
71
68
4. Exemplos
4. Exemplos
Seja x m a distância do observador até a
parede, θ a medida em radianos do ângulo segundo
o qual o observador vê o quadro, α a medida do
ângulo em radianos, segundo o qual o observador vê
a parte da parede acima do nível dos olhos e abaixo
do quadro, e β = α + θ.
Queremos encontrar o valor de x que irá
tornar θ um máximo absoluto. Como x está no
intervalo (0, +∞), o valor máximo absoluto de θ será
um valor máximo relativo.
69
A solução -2,45 foi rejeitada por não estar
no intervalo (0, +∞). Os resultados do teste da
derivada primeira estão na tabela abaixo. Como o
valor máximo relativo de θ é um valor máximo
absoluto, concluímos que o observador deve ficar a
aproximadamente 2,45 m da parede.
Conclusão
0 < x < 2,45
+
x = 2,45
0 (θ tem um valor máximo relativo)
2,45 < x < ∞
72
12