1 ) Quando a razo entre dois valores correspondentes de duas

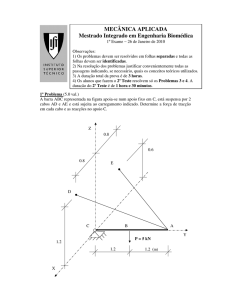
Universidade Tecnológica Federal do Paraná UTFPR
Disciplina de Física I
Prof. Nelson Elias
36ª Lista de Exercícios: Cap.11 Rotação/Energia Cinética nas Rotações/Momento de Inércia.
Aluno: ___________________________ Turma: _______ Data: ______/_____/________.
1) Dois cilindros sólidos uniformes, cada um girando em torno do seu eixo (longitudinal) central, têm a mesma massa de
1,25 kg e giram com a mesma velocidade angular de 235 rad/s, mas eles possuem raios diferentes. a) Qual a energia
cinética de rotação do cilindro menor de raio 0,25 m? b) qual a energia cinética de rotação do cilindro maior raio 0,75 m?
2) a) Calcule o momento de inércia de uma barra delgada de ferro de 2 m de comprimento e 8,7 kg de massa, em torno de
um eixo perpendicular à barra e localizado a 30 cm do centro da barra. O momento de inércia é uma grandeza escalar ou
vetorial e qual sua unidade?
2m
b) Considere uma barra rígida uniforme de massa M e comprimento L e utilize o teorema dos eixos paralelos para
mostrar que o momento de inércia dessa barra em relação a um eixo que lhe é perpendicular e passa por uma de suas
2
extremidades pode ser dado por: I = 1/3 ML
3) A figura a seguir mostra dois blocos de massa m suspensos nas extremidades de uma haste rígida, de peso desprezível,
de comprimento L = L1 + L2, com L1 = 20cm e L2 = 80cm . A haste é mantida na posição horizontal e então solta.
Calcule a aceleração dos dois blocos quando eles começam a se mover.
L
L
1
2
m
m
Torque & produto vetorial.
4) Determine o torque produzido pela força F em cada uma das situações indicadas na figura.
a) F1 = 10N,
b) F2 = 20N, c) F3 = 10N,
d) F4 = 20N
10 cm
F2
F1
30º
5) Uma pessoa tenta deslocar uma pedra com auxílio de uma
alavanca de 1 m. Para isso, ela apoia a alavanca sobre uma
pedra menor, a 20 cm da pedra grande (veja a figura). Se a pessoa
F
exercer uma força de 40 kgf perpendicularmente sobre a
alavanca, qual a força que vai agir sobre a pedra maior?
F3
5 cm
F4
30 cm
6) Binário: sistema composto por duas forças paralelas de mesma intensidade e sentidos contrários. Determine o
momento do binário nas situações representadas abaixo.
a)
b)
F = 20 N
F = 20 N
F = 20 N
30º
16 cm
7) Um bloco de gelo de 12 kg em forma de um cubo de
0,24 m de aresta está no primeiro octante de um sistema
de coordenadas, conforme figura. Calcule o torque
devido ao peso do bloco, em relação ao vértice na
origem.
y
F = 20 N
8) A figura mostra um disco uniforme, com massa M = 2,0 kg e raio R = 15 cm, montado
sobre um eixo mecânico horizontal fixo. Um bloco de massa m = 4,2 kg está pendurado na
extremidade de uma corda de massa desprezível que está enrolada em torno da borda do
disco. A corda não escorrega no disco e não há atrito no eixo.
M
Determine:
a) a aceleração do bloco em queda,
z
b) a aceleração angular do disco e
c) a tração na corda.
m
O
0,24 m
x
Respostas:
1. Resp. a) Kr = 1.078,6 J e b) 9.700 J
2. Resp. I = 3,683 kg.m2
3. Resp. a1 = 1,72 m/s2 e a2 = 6,91 m/s2
4. Resp. τ1 = - 1 N.m, τ2 = + 2,5 N.m, τ3 = 0, τ4 = 5
N.m,
5. Resp. F = 1568N
6. Resp. a) τ = - 3,2 N.m, b) τ = 1,6 N.m,
7. Resp. τ = 14,1 N.m i - 14,1 N.m j
8. Resp. a =7,9 m/s2, α = 52,66 rad/s2 e T = 7,9 N
Exercícios sobre 2ª Lei de Newton Para Rotação:
1) A figura mostra um disco uniforme, com massa M = 2,5 kg e raio R = 20 cm, montado sobre um eixo mecânico
horizontal fixo. Um bloco de massa m = 1,2 kg está pendurado na extremidade de uma corda de massa desprezível que
está enrolada em torno da borda do disco. A corda não escorrega no disco e não há atrito no eixo.
M
Determine:
a) a aceleração do bloco em queda,
b) a aceleração angular do disco,
c) a tração na corda,
d) qual a energia cinética de rotação do disco em t = 2,5s ?
(utilize: Kr = ½ Iω2 e W = τΔθ)
m
2) Um cilindro que possui uma massa de 2,0 kg pode girar em torno de seu eixo central que passa pelo ponto O. Quatro
forças são aplicadas como mostrado na figura abaixo. F1 = 6,0 N, F2 = 4,0 N, F3 = 2,0 N e F4 = 5,0 N. Além disso
R1 = 5,0 cm e R2 = 12 cm. Determine a intensidade, a direção e o sentido da aceleração angular do cilindro. (Durante a
rotação, as forças mantêm os mesmos ângulos em relação ao cilindro.)
3) Uma bicicleta é montada de modo que a roda traseira possa girar
livremente. A corrente aplica uma força de 18 N ao pinhão de força,
a uma distância rPINHÃO = 7 cm do eixo da roda.
Considere que a roda seja um aro (I = MR2) de raio
R = 35 cm e massa M = 2,4 kg.
Qual a velocidade angular da roda depois de 5 s?
4) Uma barra uniforme de comprimento L e massa M é livre para girar ao redor de um pivô sem atrito passando por uma
extremidade livre (conforme figura abaixo). A barra é solta do repouso na posição horizontal. (a) Qual a velocidade
angular da barra na sua posição mais baixa? (b) Determine a velocidade tangencial do centro de massa e a velocidade
tangencial do ponto mais baixo sobre a barra na posição vertical.
5) Dois blocos como mostrado na figura abaixo, estão ligados por um fio de massa desprezível passando sobre uma polia
de raio 0,250 m e momento de inércia I. O bloco sobre o plano inclinado sem atrito está subindo com uma aceleração
constante de 2,0 m/s2. a) Determine T1 e T2 as tensões nas duas partes do fio. b) Encontre o momento de inércia da
polia.
Respostas 2º Lei para rotação:
1. a) Resp. a = 4,8 m/s2.
b) Resp. α = 24,0 rad/s2
c) Resp. T = 6,0 N.
d) Resp. Kr = 90 J. (utilize: Kr = ½ Iω2 e W = τΔθ)
2. Resp. α = 9,7 rad/s2.
3. Resp. ω = 21,4 rad/s.
4. Resp.: a) ω = (3g L-1)1/2, vcm = 1/2(3g L)1/2 e vP = (3g L)1/2
5. Resp.: a) T1 = 118 N , T2 = 156 N e b) I = 1,17 kg m2