MECÂNICA APLICADA Mestrado Integrado em Engenharia

MECÂNICA APLICADA
Mestrado Integrado em Engenharia Biomédica
1º Exame − 26 de Janeiro de 2010
Observações:
1) Os problemas devem ser resolvidos em folhas separadas e todas as
folhas devem ser identificadas.
2) Na resolução dos problemas justificar convenientemente todas as
passagens indicando, se necessário, quais os conceitos teóricos utilizados.
3) A duração total da prova é de 3 horas.
4) Os alunos que fazem o 2º Teste resolvem só os Problemas 3 e 4. A
duração do 2º Teste é de 1 hora e 30 minutos.
1º Problema (5.0 val.)
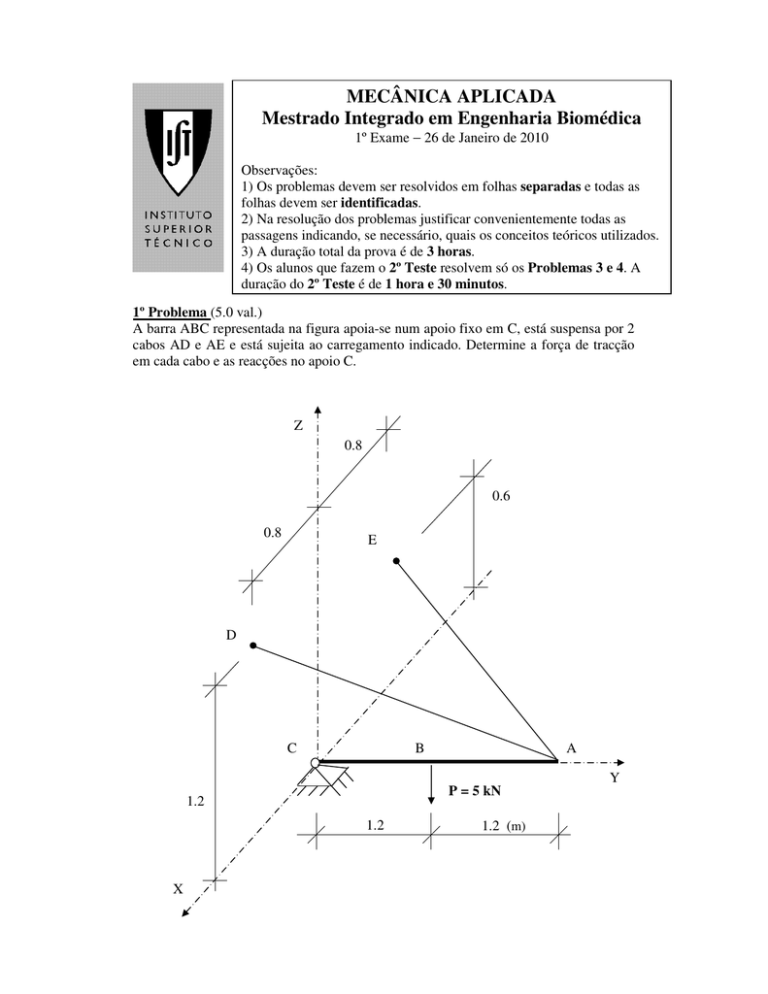
A barra ABC representada na figura apoia-se num apoio fixo em C, está suspensa por 2
cabos AD e AE e está sujeita ao carregamento indicado. Determine a força de tracção
em cada cabo e as reacções no apoio C.
Z
0.8
0.6
0.8
E
D
C
B
P = 5 kN
1.2
1.2
X
A
1.2 (m)
Y
2º Problema (5.0 val.)
Considere a estrutura representada na figura.
2 kN/m
1 kNm
C
B
D
A
2.0 (m)
1.0
1.0
(2.0) (a) Calcule as reacções de apoio.
(3.0) (b) Trace os diagramas de esforços internos indicando todos os valores necessários à sua
perfeita definição.
3º Problema (5.0 val.)
Considere o disco homogéneo de massa M = 200 Kg representado na figura.
Y
Y’
X
O
45 º
G
X’
0.1 (m)
0.2
0.5
(1.5) (a) Calcule as coordenadas do seu centro de massa G no referencial X, Y.
(2.0) (b) Calcule as componentes da respectiva matriz de inércia no ponto O.
(1.5) (c) Calcule as componentes da respectiva matriz de inércia em G no referencial X’,Y’.
Nota: Se não fez a alínea b) considere
[I]
0
( x, y)
10 0 0 
=  0 40 0  Kgm 2 .
 0 0 50
4º Problema (5.0 val.)
O sistema representado na figura é constituído por um disco homogéneo de massa 3M e
raio R e uma barra homogénea AB de massa M e comprimento 3R. O disco roda em
torno do ponto fixo C e a extremidade A da barra, à qual se encontra ligada uma mola de
rigidez K, desliza sem atrito numa guia horizontal. A mola encontra-se indeformada na
posição θ = 0. O sistema é libertado do repouso quando θ = π/2. Particularize para os
dados: R = 0.25 m, M = 10 Kg, K = 1000 N/m e g = 10 m/s2.
(1.0) a) Relacione as componentes da aceleração do centro de massa da barra e a aceleração
angular da barra com a aceleração angular do disco na configuração inicial (θ = π/2).
(2.0) b) Estabeleça o sistema de 6 equações independentes que permitem calcular as 6
incógnitas (reacção vertical em A, componentes horizontal e vertical da força de
ligação em B, reacções no ponto fixo C e aceleração angular do disco) na
configuração inicial (θ = π/2) e determine a aceleração angular do disco nesse
instante.
(2.0) c) Determine o valor da velocidade do ponto A quando θ = π/4.
(Sugestão: utilize o teorema das forças vivas e determine a posição do centro
instantâneo de rotação da barra quando θ = π/4).
g
K
3M
A
C
M
3R
R
θ
B