partículas partículas -pelo um

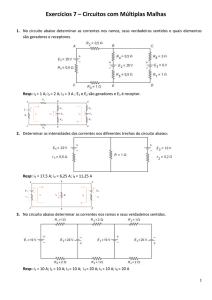
1) Determine o centro de massa de uma casca semi-esférica de raios R1 e R2 (R1>R2).
Y
Resp: ZCM= 3(R14-R24)/[8(R13-R23)]

2) Determine o Centro de massa de um arame de massa m dobrado em arco de círculo de
ângulo  e raio a.
x
Resp: XCM= (2a/)sen(/2) ; YCM = 0
3) Um projétil é lançado segundo um ângulo de 45º com energia cinética E o. Quando atinge o ponto mais alto da trajetória, ele
explode em dois fragmentos com uma energia adicional Eo . Um dos fragmentos, de massa m1, sai verticalmente para baixo.
Determine a velocidade (módulo, direção e sentido) do segundo fragmento de massa m 2. Qual a velocidade do fragmento de
massa m1.
Resp: v1  
Eo (2m2  m1 )
m1 (m1  m2 )
; v2 
Eo (4m1  m2 )
m2 (m1  m2 )
; tgθ 
vy
vx

m1 (2m2  m1 )
(m1  m2 )
4) Uma partícula de massa m1 e velocidade u1 colide com outra partícula de massa m2 em repouso. As partículas ficam coladas
após o choque. Qual a fração da energia cinética inicial é perdida na colisão?
Resp: m2/(m1+m2)
5) Uma bola de Tênis de 60g de massa bate na raquete de um jogador com velocidade de 8m/s e sai com
velocidade de 16m/s.
a) Qual o impulso sofrido pela bola?
Resp: I= (-0,09ux+1,27uy) N.s
15o
45o
Eixo Y na direção da normal.
b) Se a duração do impacto da bola com a raquete foi de 0,01 s, qual a força média que a raquete fez sobre a
bola? Resp: F = -(9ux+127uy) N
6) Quando um tiro é disparado, a explosão da pólvora expulsa a bala com uma força muito grande mas que cessa depois de
certo empo e permanece nula após. Suponha que esta força seja dada por F= (360 - 107 t2 ) até chegar a zero. A massa da bala é
3g. (a) Qual o Impulso na bala? (b) Qual a velocidade de saída da bala?
Resp: 1,44 kg.m/s e 480 m/s
7) Uma bola de borracha cai verticalmente de uma altura h 1, a partir do repouso, choca-se com o chão e sobe a uma altura h2.
Qual o coeficiente de restituição ? Qual a a fração da energia cinética é perdida em termos de ? Resp: (h2/h1)1/2; 1 - 2
8) Um jato de líquido é dirigido contra uma superfície segundo um ângulo com a normal. Após atingir a superfície o líquido se
espalha sobre ela. Sabendo que a densidade do líquido é  e sua velocidade é v, determine a pressão sobre a superfície.
Resp: p= v2 cos2
9) Na figura, m1= 4 kg, m2 = 6kg, v1 = 2 m/s e v2 = 3m/s. Determine o momento angular total do
sistema em relação a O e em relação ao centro de massa e verifique a relação entre eles.
v1
m1
Resp: 48 m2.kg/s e 14,4 m2kg/s
3m
v2
v3= 2 m/s
m3= 0,5 kg
0,3 m
30o
m
m1= 4 kg
kg
vf= 1 m/s
m2= 2 kg
4m
m2
10) Duas partículas, de massas m1 e m2, são ligadas por uma haste de comprimento
0,3 m e massa desprezível. O conjunto está sobre um plano horizontal liso. Uma
terceira partícula, de massa m3= 0,5 kg, colide com a massa m2 e sai com velocidade
vf= 1m/s, conforme mostra a figura. Determine a velocidade do centro de massa das
duas partículas ligadas.
Resp: (0,167ux – 0,083uy)m/s