g 10m/s = e) 12,5 g 10,0 m / s , = a) 10,0 m / s b) 6,0 m / s c) 3,0 m

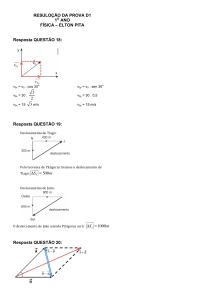
1. (Pucrj 2015) Uma bola é lançada com velocidade horizontal de 2,5 m / s do alto de um edifício e alcança o solo
a 5,0 m da base do mesmo.
Despreze efeitos de resistência do ar e indique, em metros, a altura do edifício.
Considere: g  10 m / s2
a) 10
b) 2,0
c) 7,5
d) 20
e) 12,5
2. (Mackenzie 2015) Vários corpos idênticos são abandonados de uma altura de 7,20m em relação ao solo, em
intervalos de tempos iguais. Quando o primeiro corpo atingir o solo, o quinto corpo inicia seu movimento de queda
livre. Desprezando a resistência do ar e adotando a aceleração da gravidade g  10,0 m / s2, a velocidade do
segundo corpo nessas condições é
a) 10,0 m / s
b) 6,0 m / s
c) 3,0 m / s
d) 9,0 m / s
e) 12,0 m / s
3. (Ufpr 2015) Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80m, antes de
abrir o paraquedas. Quando este se abre, ele passa a sofrer uma desaceleração vertical de 4m / s2 , chegando ao
solo com uma velocidade vertical de módulo 2m / s. Supondo que, ao saltar do avião, a velocidade inicial do
paraquedista na vertical era igual a zero e considerando g  10m / s2, determine:
a) O tempo total que o paraquedista permaneceu no ar, desde o salto até atingir o solo.
b) A distância vertical total percorrida pelo paraquedista.
4. (Uel 2015) Observe o aspersor de impulso para jardim representado na figura a seguir.
Esse aparelho possui um orifício circular de saída de 2 mm de diâmetro, e seu bico faz um ângulo de 30 com a
horizontal. Esse aspersor, quando colocado em funcionamento, fica no nível do chão e lança o jato de água em
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
um movimento parabólico que alcança o chão a uma distância de 3m. Considere que a velocidade da água na
mangueira até o aspersor é desprezível, com relação à velocidade de saída da água do aparelho, e que a
velocidade de saída da água do aspersor é v. Despreze a resistência do ar.
Dados: densidade da água p  1000
g  10
m
s2
kg
m3
; cos(30)  0,87; sen(30)  0,5; pressão atmosférica  1,01 105 Pa;
.
Com base no enunciado, calcule
a) a velocidade de saída da água do aspersor;
b) a diferença de pressão necessária para o jato de água alcançar os 3 m. Justifique sua resposta apresentando
todos os cálculos realizados.
5. (Upf 2015) Na Copa do Mundo de 2014, alguns gols foram marcados a partir de cobranças de falta. Nessa situação,
considere que um jogador bate uma falta de modo que a velocidade inicial da bola forma um ângulo de 45 com o plano do
gramado. Depois de 2 s de voo no ponto mais alto de sua trajetória, a bola bate na parte superior da trave, que está a
2,4 m do plano do gramado. Considerando g  10 m / s2 e desprezando os efeitos do atrito com o ar, pode-se dizer que a
distância, em metros, do ponto onde foi batida a falta até a trave, é de, aproximadamente:
a) 22
b) 32
c) 42
d) 52
e) 62
6. (Ufrgs 2015) Em uma região onde a aceleração da gravidade tem módulo constante, um projétil é disparado a partir do
solo, em uma direção que faz um ângulo α com a direção horizontal, conforme representado na figura abaixo.
Assinale a opção que, desconsiderando a resistência do ar, indica os gráficos que melhor representam, respectivamente, o
comportamento da componente horizontal e o da componente vertical, da velocidade do projétil, em função do tempo.
a) I e V.
b) II e V.
c) II e III.
d) IV e V.
e) V e II.
7. (Ime 2015)
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Uma mola comprimida por uma deformação x está em contato com um corpo de massa m, que se encontra
inicialmente em repouso no Ponto A da rampa circular. O corpo é liberado e inicia um movimento sem atrito na
rampa. Ao atingir o ponto B sob um ângulo θ indicado na figura, o corpo abandona a superfície da rampa. No
ponto mais alto da trajetória, entra em contato com uma superfície plana horizontal com coeficiente de atrito
cinético μ. Após deslocar-se por uma distância d nesta superfície horizontal, o corpo atinge o repouso.
Determine, em função dos parâmetros mencionados:
a) a altura final do corpo Hf em relação ao solo;
b) a distância d percorrida ao longo da superfície plana horizontal.
Dados:
- aceleração da gravidade: g;
- constante elástica da mola: k;
- raio da rampa circular: h.
8. (Imed 2015) Considere um lançador de bolinhas de tênis, colocado em um terreno plano e horizontal. O
lançador é posicionado de tal maneira que as bolinhas são arremessadas de 80 cm do chão em uma direção que
faz um ângulo de 30 graus com a horizontal. Desconsiderando efeitos de rotação da bolinha e resistência do ar, a
bolinha deve realizar uma trajetória parabólica. Sabemos também que a velocidade de lançamento da bolinha é de
10,8 km h. Qual é o módulo da velocidade da bolinha quando ela toca o chão? Se necessário, considere que a
aceleração da gravidade seja igual a 10 m s2 e que uma bolinha de tênis tenha 50 g de massa.
a) 3 m s.
b) 5 m s.
c) 6 m s.
d) 14,4 km h.
e) 21,6 km h.
TEXTO PARA A PRÓXIMA QUESTÃO:
Recentemente, uma equipe de astrônomos afirmou ter identificado uma estrela com dimensões comparáveis às
da Terra, composta predominantemente de diamante. Por ser muito frio, o astro, possivelmente uma estrela anã
branca, teria tido o carbono de sua composição cristalizado em forma de um diamante praticamente do tamanho
da Terra.
9. (Unicamp 2015) Considerando que a massa e as dimensões dessa estrela são comparáveis às da Terra,
espera-se que a aceleração da gravidade que atua em corpos próximos à superfície de ambos os astros seja
constante e de valor não muito diferente. Suponha que um corpo abandonado, a partir do repouso, de uma altura
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
h  54 m da superfície da estrela, apresente um tempo de queda t  3,0 s. Desta forma, pode-se afirmar que a
aceleração da gravidade na estrela é de
a) 8,0 m / s2.
b) 10 m / s2.
c) 12 m / s2.
d) 18 m / s2.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Gabarito:
Resposta da questão 1:
[D]
A situação representa um lançamento horizontal e desmembrando este movimento temos um movimento de
queda livre na vertical e movimento uniforme na horizontal.
No eixo horizontal (x), temos um MRU:
x  x0  v x  t
Donde tiramos o tempo de queda, usando o alcance e a velocidade horizontal:
5  0  2,5  t
t2 s
No eixo vertical (y), para a altura em função do tempo, temos a expressão:
hg
t2
2
Com os dados fornecidos e o tempo calculado:
h  10 m / s2 
 2 s2
2
 20 m
Resposta da questão 2:
[D]
Calculando o tempo de queda:
h
1 2
g t q  tq 
2
2h

g
2  7,2
10
 1,44  t q  1,2 s.
A figura mostra os cinco corpos e o tempo (t) de movimento de cada um deles.
A velocidade do 2º corpo é:
v  v0  g t  v  0  10  0,9  
v  9 m/s.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Resposta da questão 3:
a) Tempo total do salto até atingir o solo: t  t1  t2
No primeiro momento, na queda livre do paraquedista.
ΔS1  v o  t 
80 
a  t12
2
10  t12
2
t12  16
t1  4 s
Encontrando a velocidade no final do primeiro momento,
v1  v o  a  t1
v1  10  4
v1  40 m s
Assim, achando o tempo do segundo momento, temos que:
v 2  v1  a  t 2
2  40  4  t 2
t 2  9,5 s
Por fim, o tempo total será:
t  t1  t 2  4  9,5
t  13,5 s
b) A distância total percorrida: ΔSt  ΔS1  ΔS2
A distância percorrida no primeiro momento foi dada no enunciado (80 m). Para o segundo momento, temos
que:
v 22  v12  2  a  ΔS2
22  402  2   4   ΔS2
402  22
8
ΔS2  199,5 m
ΔS2 
Logo,
ΔSt  80  199,5
ΔSt  279,5 m
Resposta da questão 4:
a) A água que sai do aspersor percorre uma trajetória parabólica para um observador inercial, de acordo com
os lançamentos oblíquos, podemos decompor a velocidade inicial oblíqua nas componentes horizontais (eixo x)
e verticais (eixo y) tratando o problema como dois problemas separados. No eixo x temos o módulo da
velocidade constante, ou seja, MRU e no eixo y a velocidade varia com o tempo devido a aceleração da
gravidade e trataremos com MRUV ou ainda como lançamento vertical para cima. Temos que encontrar a
velocidade inicial de acordo com a figura abaixo, sendo dados o alcance (x) e o ângulo de lançamento,
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Decompondo a velocidade inicial em seus módulos horizontal e vertical:
Em x:
v0x  v0  cosθ
Aplicando MRU em x:
x
v0x 
t tot
Onde
x  alcance máximo horizontal e
t tot  tempo total de movimento desde a saída do aspersor até o jato de água tocar o solo.
Em y:
v0y  v0  senθ
Por simetria, notamos que este tempo total representa o dobro do tempo para que o jato de água atinja a altura
máxima. Este tempo pode ser calculado através do eixo y tomando o referencial positivo para cima e usando a
equação do MRUV:
v y  v0y  gt
Sabendo que na altura máxima v y  0, o tempo para atingir a altura máxima será:
v0y v0  sen θ
t

g
g
Então
v0x 
x
t tot
v0  cos θ 
x
t tot
v0  cos θ 
x
2t
v0  cos θ 
x
v0  sen θ
2
g
Isolando a velocidade inicial
xg
v0 
2  cos θ  sen θ
Substituindo os valores fornecidos temos a velocidade de lançamento
m
3m  10 2
30
m
s
v0 

 5,87
2  cos30  sen30
2  0,87  0,5
s
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
b) Para calcularmos a diferença de pressão devemos usar a equação de Bernoulli aplicada a dois pontos. Um
ponto próximo à saída e outro logo após o jato d’água sair do aspersor.
Considerando que o aspersor está ao nível do chão, podemos dizer que não existe diferença significativa de
altura entre a saída do jato de água e o solo, temos:
p1  p0 
ρ  v2
2
Onde:
p1  pressão interna na mangueira (Pa)
p0  pressão atmosférica (Pa)
ρ  massa específica da água (1000kg m3 )
v  velocidade da saída da água (m s)
A diferença de pressão (Δ p) será
Δ p  p1  p0 
2
ρ v

2
1000
kg 
m
 5,87 
3 
s
m
2
2
Δ p  17241Pa
Obs.: O valor é mais exato, quanto maior o número de casas decimais utilizadas no cálculo para a velocidade
obtida anteriormente. Neste caso, foi usado v  5,8722m s.
Resposta da questão 5:
[A]
Lançamento oblíquo
Não utilizando-se a informação errônea de que o ponto mais alto da trajetória é 2,4 m, chega-se a resposta do
problema.
No eixo vertical y, a equação da posição com o tempo é dada por: y  y0  v0y  t 
Substituindo-se os valores fornecidos e sabendo que y0  0
2,4  0  v0y  2 
10 2
2,4  20
 2  v0y 
 11,2 m / s
2
2
Como o ângulo de lançamento é de 45, v0y  v0x
Então a distância horizontal x é dada por: x  x0  v0x  t
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
g 2
t
2
Fazendo as substituições, tem-se: x  0  11,2  2  x  22,4 m
Correspondendo, portanto a alternativa [A]. (mas a questão poderia ter outra resposta usando-se a informação
dada no problema).
Observação: Questão de lançamento oblíquo com sério problema de enunciado, pois dá margem a interpretação
errada por parte do estudante e, portanto na minha opinião esta questão deveria ser anulada.
O fato de mencionar que 2,4 m é o ponto mais alto da trajetória poderia dar margem à seguinte interpretação:
No ponto mais alto da trajetória, a velocidade no eixo vertical é nula e obedece a seguinte equação: v y  v0y  gt
Substituindo os valores: 0  v0y  10  2  v0y  20 m / s
E sabendo que v0x  v0y devido ao ângulo de 45, podemos calcular a distância no eixo horizontal com a
equação: x  x0  v0x  t
Substituindo os valores: x  0  20  2  40 m (incorrendo em um erro decorrente da informação do enunciado dar
margem à dúvidas de interpretação).
Por outro lado, usando-se v0y  11,2 m / s, podemos descobrir qual foi a altura máxima com o tempo de subida:
v y  v0y  gt
0  11,2  10t  tsub 
11,2
 1,12 s
10
E agora calcular a altura máxima real
g
y  y0  v0y  t   t 2
2
10
y  0  11,2  1,12 
 1,122  y  6,27 m
2
Logo, a informação fornecida no enunciado é equivocada e trás confusão para a resolução correta da questão. A
bola antes de bater no travessão está na descendente, ou seja, já passou do ponto de altura máxima. Sendo
assim, não se trata de uma boa questão para ser utilizada a menos que se façam correções no texto da mesma.
Resposta da questão 6:
[B]
As equações dessas componentes são:

v x  constante  reta horizontal  gráfico II .


v y  v0y  gt  reta decrescente  gráfico  V  .
Resposta da questão 7:
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711

vBx  vB cos θ
Na figura: 

vBy  vB sen θ
a) Usando a conservação da energia mecânica entre os pontos A e B, calculamos a velocidade em B:
A
Emec
 EB
mec 
k x2
m vB2
 m g hA 
 mg hB 
2
2
k x2
m vB2
m gh 
 m g h  hcos θ 
2
2
vB2 
k x2
 2 g hcos θ.
m
A partir do ponto B, temos um lançamento oblíquo com altura máxima hf em relação ao ponto de lançamento.

2
v 2y  vBy
 2 g hf  0  vB sen θ
 k x2
 sen2θ
hf  
 2g hcos θ 
 m
 2g



2
 2 g hf
v 2 sen2θ
 hf  B
2g

 k x2

 hf  
 hcos θ  sen2θ.
 2mg



Da figura:
 k x2

Hf  hf  h 1  cos θ  Hf  
 hcos θ  sen2θ  h 1  cos θ
 2mg



Hf 
k x2
sen2θ  hcos θ sen2θ  h 1  cos θ 
2mg
Hf 
k x2
sen2θ  h cos θ 1  cos2 θ  1  cos θ 


2mg
Hf 




k x 2 sen2θ
 h 1  cos3 θ .
2mg
b) O movimento na superfície plana horizontal tem velocidade inicial vC  vBx  vB cosθ e velocidade final
vD  0.
Entre os pontos C e D a força resultante é a força de atrito. Aplicando o teorema da energia cinética entre esses
pontos:
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
C
WFat  ED
cin  Ecin   Fat d 
μ mg d  0 
m  vB cos θ
2
2
m vC
m vD

2
2
2
2
 d

1 2
v cos2 θ 
2μ g B

1  k x2
 2 g hcos θ  cos2 θ 


2μ g  m

d
 k x2
hcos θ 
d 

 cos2 θ.
 2 μ mg

μ


Resposta da questão 8:
[B]
Dados:
h  0,8 m
θ  30
vo  3 m s
g  10m s2
m  50 g  0,05 kg
Tem-se a seguinte situação,
Em relação a energia, pode-se dizer que em 1 a bolinha de tênis possui tanto energia cinética como energia
potencial gravitacional (relacionado a altura h) e na posição 2 a bolinha terá somente energia cinética.
Como pede-se para desconsiderar efeitos dissipativos de energia,
Em  Emf
i
m  v o2
m  v2
 mgh 
2
2
32
v2
 10  0,8 
2
2
v2
 4,5  8
2
v 2  2  12,5
v5 m s
Resposta da questão 9:
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
[C]
h
2 h 2  54
g 2
t  g


2
t2
32
g  12 m/s2 .
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Resumo das questões selecionadas nesta atividade
Data de elaboração:
Nome do arquivo:
21/12/2015 às 23:26
ANEXO 7 - LANÇAMENTO DE PROJÉTEIS
Legenda:
Q/Prova = número da questão na prova
Q/DB = número da questão no banco de dados do SuperPro®
Q/prova Q/DB
Grau/Dif.
Matéria
Fonte
Tipo
1 ............ 135681..... Média ............ Física .............Pucrj/2015 ............................ Múltipla escolha
2 ............ 139816..... Baixa ............. Física .............Mackenzie/2015 ................... Múltipla escolha
3 ............ 136473..... Média ............ Física .............Ufpr/2015.............................. Analítica
4 ............ 136898..... Elevada ......... Física .............Uel/2015 ............................... Analítica
5 ............ 140205..... Média ............ Física .............Upf/2015 ............................... Múltipla escolha
6 ............ 138019..... Baixa ............. Física .............Ufrgs/2015 ............................ Múltipla escolha
7 ............ 141288..... Elevada ......... Física .............Ime/2015 .............................. Analítica
8 ............ 143160..... Baixa ............. Física .............Imed/2015 ............................ Múltipla escolha
9 ............ 135833..... Baixa ............. Física .............Unicamp/2015 ...................... Múltipla escolha
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711