a) 10,2 km. b) 4,50 km. c) 14,7 km. d) 5,70 km. e) 6,00 km.

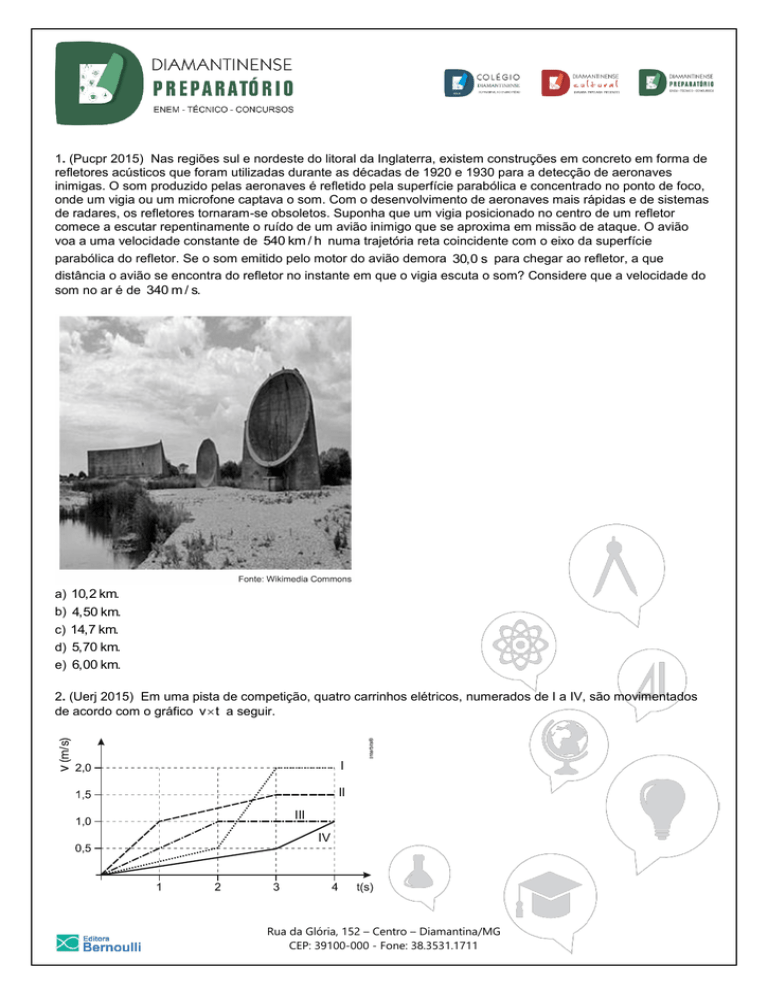
1. (Pucpr 2015) Nas regiões sul e nordeste do litoral da Inglaterra, existem construções em concreto em forma de
refletores acústicos que foram utilizadas durante as décadas de 1920 e 1930 para a detecção de aeronaves
inimigas. O som produzido pelas aeronaves é refletido pela superfície parabólica e concentrado no ponto de foco,
onde um vigia ou um microfone captava o som. Com o desenvolvimento de aeronaves mais rápidas e de sistemas
de radares, os refletores tornaram-se obsoletos. Suponha que um vigia posicionado no centro de um refletor
comece a escutar repentinamente o ruído de um avião inimigo que se aproxima em missão de ataque. O avião
voa a uma velocidade constante de 540 km / h numa trajetória reta coincidente com o eixo da superfície
parabólica do refletor. Se o som emitido pelo motor do avião demora 30,0 s para chegar ao refletor, a que
distância o avião se encontra do refletor no instante em que o vigia escuta o som? Considere que a velocidade do
som no ar é de 340 m / s.
a) 10,2 km.
b) 4,50 km.
c) 14,7 km.
d) 5,70 km.
e) 6,00 km.
2. (Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos, numerados de I a IV, são movimentados
de acordo com o gráfico v  t a seguir.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
3. (Pucmg 2015) Em um hospital, estudantes de medicina registraram o número médio de batimentos cardíacos
de pacientes de diversas idades. Os resultados foram resumidos em uma tabela conforme mostrado a seguir.
BATIMENTOS POR MINUTO
200
195
190
180
170
155
140
IDADE DO PACIENTE (ANOS)
20
25
30
40
50
65
80
Sobre essas observações, é CORRETO afirmar:
a) O período dos batimentos cardíacos diminui com a idade.
b) A frequência cardíaca aumenta com a idade.
c) A frequência e o período dos batimentos cardíacos diminuem com a idade.
d) A frequência dos batimentos cardíacos diminui com a idade enquanto o período aumenta.
4. (Ufrgs 2015) Em 2014, comemoraram-se os 50 anos do início da operação de trens de alta velocidade no Japão, os
chamados trens-bala. Considere que um desses trens desloca-se com uma
velocidade constante de 360km / h sobre trilhos horizontais. Em um trilho paralelo, outro trem desloca-se também com
velocidade constante de 360km / h, porém em sentido contrário.
Nesse caso, o módulo da velocidade relativa dos trens, em m / s. é Igual a
a) 50.
b) 100.
c) 200.
d) 360.
e) 720.
5. (Ufsc 2015) Dois amigos, Tiago e João, resolvem iniciar a prática de exercícios físicos a fim de melhorar o
condicionamento. Tiago escolhe uma caminhada, sempre com velocidade escalar constante de 0,875m / s, 300m
na direção norte e, em seguida, 400m na direção leste. João prefere uma leve corrida, 800m na direção oeste e,
em seguida, 600m na direção sul, realizando o percurso com velocidade média de módulo 1,25m / s. Eles partem
simultaneamente do mesmo ponto.
De acordo com o exposto acima, é CORRETO afirmar que:
01) o módulo da velocidade média de Tiago é 0,625m / s.
02) Tiago e João realizam seus percursos em tempos diferentes.
04) o deslocamento de Tiago é de 700m.
08) a velocidade escalar média de João é de 1,75m / s.
16) o módulo do deslocamento de João em relação a Tiago é 1500m.
32) a velocidade de João em relação a Tiago é de 0,625m / s.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
6. (Uema 2015) “[...] A distância que um atleta de futebol percorre durante uma partida é, em média, 12 km para os
homens e 10 km para as mulheres.”
Fonte: Disponível em: <http://www.univesp.ensinosuperior.sp.gov.br/>. Acesso em: 30 jun. 2014. (adaptado)
As velocidades médias, para homens e mulheres, no decorrer dos 90 min, em um jogo de futebol, são,
respectivamente,
a) 114,3 m / min e 95,2 m / min
b) 8,0 km / h e 6,7 km / h
c) 266,70 m / min e 222,2 m / min
d) 8,0 m / h e 6,7 m / h
e) 16,0 m / h e 13,4 m / h
7. (Unesp 2015) João mora em São Paulo e tem um compromisso às 16 h em São José dos Campos, distante 90
km de São Paulo. Pretendendo fazer uma viagem tranquila, saiu, no dia do compromisso, de São Paulo às 14 h,
planejando chegar ao local pontualmente no horário marcado. Durante o trajeto, depois de ter percorrido um terço
do percurso com velocidade média de 45 km / h, João recebeu uma ligação em seu celular pedindo que ele
chegasse meia hora antes do horário combinado.
Para chegar ao local do compromisso no novo horário, desprezando- se o tempo parado para atender a ligação,
João deverá desenvolver, no restante do percurso, uma velocidade média, em km / h, no mínimo, igual a
a) 120.
b) 60.
c) 108.
d) 72.
e) 90.
8. (Pucrs 2015) Considere o gráfico abaixo, que representa a velocidade de um corpo em movimento retilíneo em
função do tempo, e as afirmativas que seguem.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
I. A aceleração do móvel é de 1,0 m / s2.
II. A distância percorrida nos 10 s é de 50 m.
III. A velocidade varia uniformemente, e o móvel percorre 10 m a cada segundo.
IV. A aceleração é constante, e a velocidade aumenta 10 m / s a cada segundo.
São verdadeiras apenas as afirmativas
a) I e II.
b) I e III.
c) II e IV.
d) I, III e IV.
e) II, III e IV.
9. (Upe 2015) Duas partículas, 1 e 2, se movem ao longo de uma linha horizontal, em rota de encontro com
velocidades iniciais de módulos iguais a v1  10m / s e v2  14m / s e acelerações contrárias às suas
velocidades de módulos a1  1,0m / s2 e a2  0,5m / s2 .
Sabendo que o encontro entre elas ocorre, apenas, uma vez, o valor da separação inicial, d, entre as partículas
vale
a) 4m
b) 8m
c) 16m
d) 96m
e) 192m
10. (Imed 2015) Considere um carro que se movimenta ao longo de uma pista retilínea. O gráfico abaixo descreve
a velocidade do carro em função do tempo, segundo um observador em repouso sobre a calçada.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Em relação a essa situação, assinale a alternativa correta.
a) O movimento é uniformemente variado.
b) O carro realiza um movimento retilíneo uniforme.
c) Ao final do movimento (t  8s), o carro retorna à sua posição de origem (t  0).
d) O carro está freando no intervalo 4s  t  8s.
e) Em t  4, o carro inverte o sentido do seu movimento.
11. (Ufpr 2015) Um veículo está se movendo ao longo de uma estrada plana e retilínea. Sua velocidade em função do tempo,
para um trecho do percurso, foi registrada e está mostrada no gráfico abaixo. Considerando que em t  0 a posição do
veículo s é igual a zero, assinale a alternativa correta para a sua posição ao final dos 45s.
a)
b)
c)
d)
e)
330m.
480m.
700m.
715m.
804m.
TEXTO PARA A PRÓXIMA QUESTÃO:
Para responder à(s) questão(ões), considere as afirmativas referentes à figura e ao texto abaixo.
Na figura acima, está representada uma pista sem atrito, em um local onde a aceleração da gravidade é
constante. Os trechos T1, T2 e T3 são retilíneos. A inclinação de T1 é maior do que a inclinação de T3, e o
trecho T2 é horizontal. Um corpo é abandonado do repouso, a partir da posição A.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
12. (Pucrs 2015) Com base nessas informações, afirma-se:
I. O movimento do corpo, no trecho T1, é uniforme.
II. No trecho T3, o corpo está em movimento com aceleração diferente de zero.
III. No trecho T2, a velocidade e a aceleração do corpo têm a mesma direção e o mesmo sentido.
Está/Estão correta(s) a(s) afirmativa(s)
a) I, apenas.
b) II, apenas.
c) I e III, apenas.
d) II e III, apenas.
e) I, II e III.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Gabarito:
Resposta da questão 1:
[D]
A distância em que o avião se encontra do refletor no instante em que o vigia escuta o seu som é dado pelo tempo
que a onda sonora chega a ele descontando a distância percorrida pelo avião no mesmo tempo que a onda leva
para chegar ao seu destino.
Distância percorrida pelo som (ds ) até o observador no momento inicial t  0s.
ds  vs  t (1)
Onde:
v s  velocidade do som no ar (340 m/s) e
t  tempo para a onda sonora chegar ao observador.
E a distância que o avião percorre enquanto a onda sonora se desloca até o observador é dada por equação
semelhante:
da  va  t (2)
Onde:
da  distância percorrida pelo avião no tempo t,
va  velocidade do avião (m/s)
Sendo, va  540
km
1h
1000m
m


 150
h 3600s 1km
s
Fazendo a diferença das equações (1) e (2) temos a distância do observador do ao avião no momento em que ele
escuta o som.
do  (vs  va )  t
Resposta da questão 2:
[B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o eixo dos tempos. Calculando
cada uma delas:
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711

 2  0,5 1  1 2  0,5  1,25  2  3,75 m.
2  0,5

DI 
2
2





1,5  1 2  1,5  1  0,5  2,5  1,5  4,5 m.
1 1

DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
 IV
2
2
Resposta da questão 3:
[D]
A frequência é no número de batimentos por minuto. O período é o intervalo de tempo entre duas batidas
consecutivas, ou seja, o período é igual ao inverso da frequência.
Consultando a tabela, vemos que a frequência diminui com o aumento da idade, logo o período aumenta.
Resposta da questão 4:
[C]
Em movimentos de sentidos opostos, o módulo da velocidade relativa é igual a soma dos módulos das
velocidades.
720
| vrel |  | v1 |  | v 2 |  360  360  720 km/h 
m/s 
3,6
| vr |  200 m/s.
Resposta da questão 5:
01 + 08 + 16 = 25.
[01] (Verdadeira) O tempo gasto por Tiago foi
d
700m
t 
 800s
m
v
0,875
s
Mas como a velocidade média indica o deslocamento do móvel com o tempo
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Pelo teorema de Pitágoras tiramos o deslocamento Δs
Δs  500m
Calculando a velocidade média:
Δs 500m
m
vm 

 0,625
Δt
800s
s
[02] (Falsa) O deslocamento de João usando Pitágoras será:
Δs  1000m
O tempo gasto no percurso de João é:
Δs 1000m
t

 800s
m
vm
1,25
s
[04] (Falsa) Vimos anteriormente que o deslocamento de Tiago foi de 500m.
[08] (Verdadeira) A velocidade escalar média e dada pela distância percorrida no tempo gasto, então:
d 800m  600m 1400m
m
vm  

 1,75
t
800s
800s
s
[16] (Verdadeira) Como se verifica na figura abaixo, João fica deslocado 1500 m em relação ao Tiago.
[32] (Falsa) Como os dois se deslocam em direções opostas, a intensidade da velocidade relativa de João em
relação a Tiago é representada pela soma de seus módulos:
m
m
m
vJ,T  1,25  0,625  1,875
s
s
s
Resposta da questão 6:
[B]
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
A velocidade escalar média é dada pela razão entre a distância percorrida e o tempo gasto no percurso.
Δs
vm 
Δt
Então para os homens:
12 km 60 min
vm 

 8 km / h
90 min
1h
E para as mulheres:
10 km 60 min
vm 

 6,7 km / h
90 min
1h
Resposta da questão 7:
[D]
D  90 km

Percurso total  
3
Δt  1 e 30 min  1,5 h  2 h

1
90

 30 km
d  D 
Pr imeiro trecho   1 3
3
v  45 km/h
 1
 Δt1 
d1 30
2

 Δt1  h.
v1 45
3
d2  D  d1  90  30  d2  60 km

Segundo trecho  
3 2
5
Δt 2  Δt  Δt1  2  3  Δt 2  6 h

 v2 
d2
60


Δt 2 5
6
v 2  72 km/h.
Resposta da questão 8:
[A]
[I] Verdadeira. Aplicando a definição de aceleração escalar média:
Δv 10
a  am 

 a  1 m/s2.
Δt 10
[II] Verdadeira. O espaço percorrido é dado pela área entre a linha do gráfico e o eixo dos tempos.
10  10
ΔS 
 ΔS  50 m.
2
[III] Falsa. A velocidade é variável.
[IV] Falsa. A velocidade aumenta 1,0 m/s a cada segundo.
Resposta da questão 9:
[E]
Tomando as equações horárias das posições de cada móvel, temos:
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
1
1
s1  0  10t  t2 e s2  d  14t  t 2
2
4
Em que
S  posição de cada móvel (m) no instante t (s)
No encontro dos móveis, as posições são iguais. s1  s2
1
1
10t  t2  d  14t  t2
2
4
Rearranjando os termos
3t 2  96t  4d  0 (1)
Sabendo que o encontro ocorre apenas uma vez, temos um choque totalmente inelástico, isto é, a velocidade final
das duas partículas é a mesma.
t
v1  10  t e v 2  14 
2
v1  v 2
10  t  14 
t
48
t
 t  16 s
2
3
Substituindo o tempo encontrado na equação (1), obtemos:
3  162  96  16  4d  0  d  192m
Outra forma de pensar a resolução desta questão a partir da equação (1) é que o encontro dos móveis significa as
raízes da equação quadrática. Como esse encontro se dá uma única vez, temos duas raízes reais iguais, ou seja,
Δ  0, então:
( 96)2  4  3  4d  0
9216  48d  0
9216
d
 d  192 m
48
Resposta da questão 10:
[D]
Analisando as alternativas,
[A] INCORRETA. Em um movimento uniformemente variado, a aceleração é constante durante o movimento. O
Gráfico mostra claramente que na primeira parte do movimento o módulo da velocidade está aumentando
(aceleração maior que zero) e na segunda parte diminuindo (aceleração menor que zero). Desta forma, podese dizer que a aceleração não é constante durante o movimento.
[B] INCORRETA. Um movimento retilíneo uniforme tem aceleração nula.
[C] INCORRETA. Em momento algum do movimento descrito na figura existe uma inversão de sentido do
movimento. Logo, o carro não irá retornar a sua posição inicial.
[D] CORRETA.
[E] INCORRETA. Inverte o sentido de sua aceleração e não do movimento (velocidade).
Resposta da questão 11:
[D]
Como a posição inicial é zero, a sua posição final será exatamente igual à distância percorrida. Sabendo que a
distância percorrida é igual numericamente à área do gráfico, então:
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
ΔST  A1  A2  A3  A4  A5
Porém, para que seja possível calcular as áreas 4 e 5, é necessário encontrar o tempo em que acontece a
mudança de sentido na velocidade (ponto em que cruza o eixo x).
Sabendo que o movimento de 1 para 2 é um Movimento Retilíneo Uniformemente Variado (MRUV), podemos
analisar este intervalo de tempo para encontrar a aceleração.
v  v0  at
10  36  a  5
a  9,2 m s
Agora, analisando o trecho de 1 para 3, temos que:
v  v 0  at
0  36  9,2  t
t 3,9 s
Assim,
 15  5   28   10  28   3,9  36    6,1  5   10 
ΔST   35  8   




2
2

  2   2  

ΔST  280  280  140  70,2  55,5
ΔST  714,7 m
ΔST
715 m
Resposta da questão 12:
[B]
[I] Incorreta. O movimento do corpo no trecho T1 é acelerado.
[II] Correta. No trecho T3, o corpo está em movimento com aceleração diferente de zero, em sentido oposto ao
da velocidade, pois o movimento é retardado.
[III] Incorreta. No trecho T2, a velocidade é constante e a aceleração é nula.
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711
Resumo das questões selecionadas nesta atividade
Data de elaboração:
Nome do arquivo:
21/12/2015 às 23:08
ANEXO 4 - CINEMATICA ESCALAR=MU E MUV
Legenda:
Q/Prova = número da questão na prova
Q/DB = número da questão no banco de dados do SuperPro®
Q/prova Q/DB
Grau/Dif.
Matéria
Fonte
Tipo
1 ............ 136302..... Baixa ............. Física .............Pucpr/2015 ........................... Múltipla escolha
2 ............ 134157..... Baixa ............. Física .............Uerj/2015 .............................. Múltipla escolha
3 ............ 140307..... Baixa ............. Física .............Pucmg/2015 ......................... Múltipla escolha
4 ............ 138017..... Baixa ............. Física .............Ufrgs/2015 ............................ Múltipla escolha
5 ............ 136635..... Baixa ............. Física .............Ufsc/2015 ............................. Somatória
6 ............ 139094..... Baixa ............. Física .............Uema/2015 ........................... Múltipla escolha
7 ............ 140383..... Baixa ............. Física .............Unesp/2015 .......................... Múltipla escolha
8 ............ 139281..... Baixa ............. Física .............Pucrs/2015 ........................... Múltipla escolha
9 ............ 137702..... Média ............ Física .............Upe/2015 .............................. Múltipla escolha
10 .......... 143159..... Baixa ............. Física .............Imed/2015 ............................ Múltipla escolha
11 .......... 136464..... Média ............ Física .............Ufpr/2015.............................. Múltipla escolha
12 .......... 143168..... Baixa ............. Física .............Pucrs/2015 ........................... Múltipla escolha
Rua da Glória, 152 – Centro – Diamantina/MG
CEP: 39100-000 - Fone: 38.3531.1711