Derivadas de Ordem Superior

1. Derivadas segunda, terceira
e de ordem superior
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
Exemplo
superior
Derivadas de Ordem Superior
1: Cálculo
de derivadas de ordem
f ( x ) = 2x 4 − 3 x 2
Função original
f '( x ) = 8x3 − 6x
Derivada primeira
f '' ( x ) = 24 x 2 − 6
Derivada segunda
f ''' ( x ) = 48 x
Derivada terceira
f ( 4) ( x ) = 48
Derivada quarta
f (5) ( x ) = 0
Derivada quinta
Prof.: Rogério Dias Dalla Riva
4
1. Derivadas segunda, terceira
e de ordem superior
Derivadas de Ordem Superior
1.Derivadas segunda, terceira e de ordem superior
Notação para Derivadas de Ordem Superior
2.Aceleração
1. 1a derivada:
y' ,
f ' ( x ),
2. 2a derivada:
y'' ,
f '' ( x ),
3. 3a derivada:
y''' ,
f ''' ( x ),
4. 4a derivada:
y( 4) , f ( 4) ( x ),
5. n ma derivada:
y( n ), f ( n ) ( x ),
dy
,
dx
d 2y
,
dx 2
3
d y
,
dx 3
4
d y
,
dx 4
dny
,
dx n
d
[f ( x )],
dx
d2
[f ( x )],
dx 2
3
d
[ f ( x )] ,
dx 3
4
d
[f ( x )],
dx 4
dn
[f ( x )],
dx n
Dx [ y ]
Dx 2 [ y ]
Dx 3 [ y ]
Dx 4 [ y ]
Dx n [ y ]
5
1. Derivadas segunda, terceira
e de ordem superior
1. Derivadas segunda, terceira
e de ordem superior
A derivada de f’ é a derivada segunda de f
e se representa por f ’’.
d '
f ( x ) = f " ( x )
dx 
Exemplo 2: Ache o valor de g’’’(2) para a função
g (t ) = −t 4 + 2t 3 + t + 4.
Derivada segunda
Comecemos diferenciando três vezes.
A derivada de f’’ é a derivada terceira de f
e se representa por f’’’.
d ''
f ( x ) = f "' ( x )
dx 
Derivada terceira
Continuando o processo, obtêm-se
derivadas de ordem superior de f.
g ' (t ) = −4t 3 + 6t 2 + 1
Derivada primeira
g '' (t ) = −12t 2 + 12t
Derivada segunda
g ''' (t ) = −24t + 12
Derivada terceira
as
3
6
1
1. Derivadas segunda, terceira
e de ordem superior
2. Aceleração
Calculemos então a derivada terceira de g
em t = 2.
g ''' (2) = −24(2) + 12 = −36
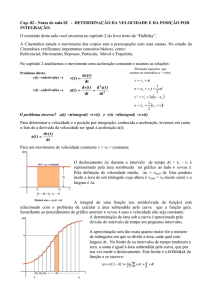
Na aula relativa a Taxas de Variação, vimos
que a velocidade de um objeto em movimento
retilíneo é dada pela derivada de sua função
posição. Em outras palavras, a taxa de variação da
posição em relação ao tempo é definida como a
velocidade. Analogamente, a taxa de variação da
velocidade em relação ao tempo é definida como a
aceleração do objeto.
Valor da derivada terceira
Os exemplos 1 e 2 mostram como achar
derivadas de ordem superior de funções
polinomiais. Note que, a cada diferenciação
sucessiva, o grau do polinômio diminui de uma
unidade. Ao final, as derivadas de ordem superior
de funções polinomiais se reduzem a uma
constante.
7
1. Derivadas segunda, terceira
e de ordem superior
10
2. Aceleração
Especificamente, a derivada de ordem n de
um polinômio de grau n
s = f (t )
f ( x ) = an x n + an −1x n −1 + … a1x + a0
ds
= f ' (t )
dt
d 2s
= f '' (t )
dt 2
é a função constante
f ( n ) = n ! an
onde n! = 1 . 2 . 3 … n. Todas as derivadas de ordem
superior a n são zero. Os polinômios são as únicas
funções com esta característica. Para outras
funções, a diferenciação sucessiva nunca resulta
em uma função constante.
Função posição
Função velocidade
Função aceleração
8
2. Aceleração
1. Derivadas segunda, terceira
e de ordem superior
Exemplo
superior
3: Cálculo
y = x −1 =
de derivadas de ordem
1
x
y ' = ( −1) x −2 = −
1
x2
2
x3
y ''' = ( −1)( −2)( −3) x −4 = −
y
Exemplo 4: Uma bola é atirada para o ar do topo
de um rochedo de 160 pés, conforme a figura a
seguir. A velocidade inicial da bola é de 40 pés/s, o
que implica que a função posição é
Função original
y '' = ( −1)( −2) x −3 =
(4)
11
= ( −1)( −2)( −3)( −4) x
6
x4
−5
24
= 5
x
Derivada primeira
s = −16t 2 + 48t + 160
Derivada segunda
onde o tempo t é dado em segundos. Ache a altura,
a velocidade e a aceleração da bola quando t = 3.
Derivada terceira
Derivada quarta
9
12
2
2. Aceleração
2. Aceleração
Inicie diferenciando, para achar as funções
velocidade e aceleração.
s = −16t 2 + 48t + 160
ds
= −32t + 48
dt
2
d s
= −32
dt 2
Função posição
Função velocidade
Para achar a função aceleração, diferenciamos a função velocidade.
Função aceleração
dv (t + 5)(80) − (80t )(1)
400
=
=
(t + 5)2
(t + 5)2
dt
13
2. Aceleração
16
2. Aceleração
Para achar a altura, a velocidade e a
aceleração quando t = 3, faça t = 3 em cada uma
das funções acima.
t (s)
0
10
20
30
40
50
60
v (pés/s)
0
53,3
64,0
68,6
71,1
72,7
73,8
dv/dt
(pés/s2)
16
1,78
0,64
0,33
0,20
0,13
0,09
s = −16(3) + 48(3) + 160 = 160 pés
2
Na tabela acima, note que a aceleração
tende para zero na medida em que a velocidade
tende a se estabilizar. Esta observação está de
acordo com a experiência: ao dirigirmos um
automóvel em aceleração, não sentimos a
velocidade, e sim a aceleração. Em outras palavras,
sentimos a variação na velocidade.
ds
= −32(3) + 48 = −48 pés/s
dt
2
d s
= −32 pés/s2
dt 2
14
17
2. Aceleração
Exemplo 5: A velocidade v (em pés/s) de um
automóvel que parte do repouso, é
v=
80t
t +5
onde t é o tempo (em s). A figura a seguir mostra a
posição do automóvel. Ache a velocidade e a
aceleração do automóvel com intervalos de 10 s, de
t = 0 a t = 60.
15
3