t(v

Cap. 02 - Notas de aula 02 - DETERMINAÇÃO DA VELOCIDADE E DA POSIÇÃO POR
INTEGRAÇÃO.
O conteúdo desta aula você encontra no capítulo 2 do livro texto do “Halliday”.
A Cinemática estuda o movimento dos corpos sem a preocupação com suas causas. No estudo da
Cinemática verificamos importantes conceitos básicos, como:
Referencial; Movimento; Repouso; Partícula; Móvel e Trajetória.
No capítulo 2 analisamos o movimento com aceleração constante e usamos as relações:
Problema direto,
x(t) →(derivada) →
v(t) →(derivada) →
dx(t )
dt
dv(t ) d 2 x(t )
a(t ) =
=
dt
dt 2
v(t ) =
Principais equações que
usamos na cinemática a = const.
v = v 0 + at
1 2
at
2
v 2 = v 02 + 2a (x − x 0 )
x = x 0 + v0 t +
x = x0 +
1
(v 0 + v)t
2
O problema inverso? a(t) →(integral) → v(t) e v(t) →(integral) → x(t)
Para determinar a velocidade e a posição por integração, conhecida a aceleração, levamos em conta
o fato de a derivada da velocidade ser igual à aceleração a(t).
dv(t )
a( t ) =
dt
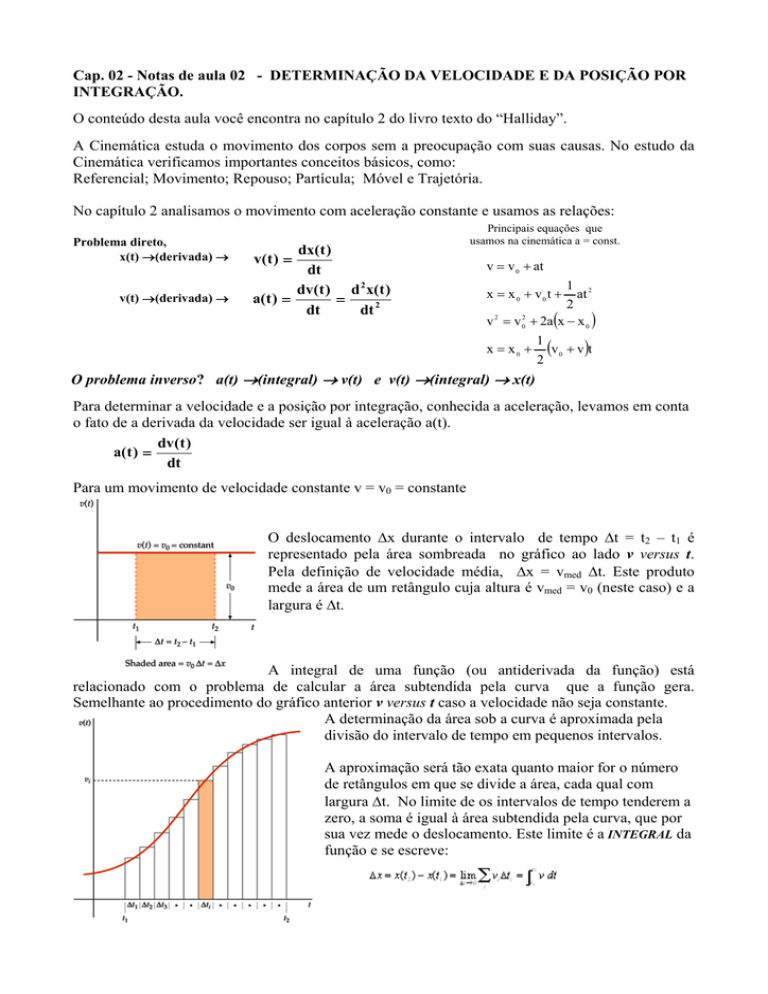
Para um movimento de velocidade constante v = v0 = constante
O deslocamento Δx durante o intervalo de tempo Δt = t2 – t1 é
representado pela área sombreada no gráfico ao lado v versus t.
Pela definição de velocidade média, Δx = vmed Δt. Este produto
mede a área de um retângulo cuja altura é vmed = v0 (neste caso) e a
largura é Δt.
A integral de uma função (ou antiderivada da função) está
relacionado com o problema de calcular a área subtendida pela curva que a função gera.
Semelhante ao procedimento do gráfico anterior v versus t caso a velocidade não seja constante.
A determinação da área sob a curva é aproximada pela
divisão do intervalo de tempo em pequenos intervalos.
A aproximação será tão exata quanto maior for o número
de retângulos em que se divide a área, cada qual com
largura Δt. No limite de os intervalos de tempo tenderem a
zero, a soma é igual à área subtendida pela curva, que por
sua vez mede o deslocamento. Este limite é a INTEGRAL da
função e se escreve:
A regra geral para integração de uma função que seja potência de t é:
tn+1
∫0 t dt = n + 1 + C
t
n
A constante de integração está relacionada ás condições iniciais do problema.
Exemplos:
1) Calculo da posição a partir da velocidade constante (numa dimensão)
t
x(t) = ∫ v(t)dt
v(t) →(integral) → x(t)
0
A constante de integração C = x0 é igual à posição inicial.
t
x(t) = x0 + ∫ v(t)dt
0
Calculo da velocidade a partir da aceleração.
a(t) →(integral) → v(t)
t
r
r
v(t) = v0 + ∫ a(t)dt
0
A constante de integração é obtida considerando t = 0.
t
Assim:
r
r
v(t) = ∫ a(t)dt = at + C
0
Com t = 0 a equação acima fica:
t
r
r
v(0) = ∫ a(t)dt
= a0 + C
0
v(0) = v0 velocidade inicial que é uma das condições iniciais do problema.
Para um movimento onde a aceleração
seja constante podemos considerar:
t
r
v(t) = v0 + at
x(t) = ∫ (v0 + at) dt
0
O que resulta na conhecida equação horária do MRUV.
1
x(t) = C+ v0 t + at2
2
A constante de integração é a posição inicial x0
1
x(t) = x0 + v0 t + at2
2