Aula 20

MATEMÁTICA
1° ANO
ENSINO MÉDIO
PROF. ALEXANDRE DOS SANTOS
PROF. EMERSON MARÃO
CONTEÚDOS E HABILIDADES
Unidade IV
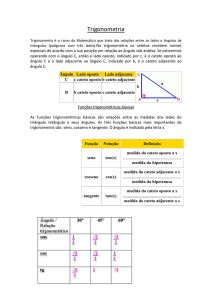
Trigonometria
2
CONTEÚDOS E HABILIDADES
Aula 20.2
Conteúdo
Seno, cosseno e tangente
3
CONTEÚDOS E HABILIDADES
Habilidade
Utilizar as relações, seno, cosseno e tangente na resolução
de problemas.
4
REVISÃO
CO
Sen α=
H
CA
Cos α=
H
5
DESAFIO DO DIA
Um avião se encontra a 600 m de altura quando avista a
cabeceira da pista onde irá pousar sob um ângulo de declive
de 30°. A que distância o avião está da cabeceira da pista?
30
600m
o
x
30
o
pista
6
AULA
Tangente: razão entre o cateto oposto a um ângulo de um
triângulo retângulo e o cateto adjacente.
Hipotenusa
60
o
Cateto
oposto
a 30o
30
o
cateto oposto a 30º
Tg 30º =
cateto adjacente a 60º
cateto oposto a 60º
Tg 60º =
cateto adjacente a 30º
Cateto oposto a 60o
Tg α =
CO
CA
7
AULA
Exemplo:
(Ufjf ) Um topógrafo foi chamado para obter a altura de
um edifício. Para fazer isto, ele colocou um teodolito
(instrumento ótico para medir ângulos) a 200 metros do
edifício e mediu um ângulo de 30°, como indicado na figura
a seguir. Sabendo que a luneta do teodolito está a 1,5
metros do solo, pode-se concluir que, dentre os valores
adiante, o que melhor aproxima a altura do edifício, em
metros, é:
8
AULA
Use os valores:
sen30° = 0,5
cos30° = 0,866
tg30° = 0,577
a) 112
b) 115
c) 117
d) 120
e) 124
9
AULA
Resolução: Conforme os dados do problema, temos: o
cateto adjacente ao ângulo de referência (a distância entre
o teodolito e o edifício) devemos obter a altura do edifício
(cateto adjacente), mais a altura do instrumento ótico para
medir ângulos (teodolito), portanto a razão trigonométrica
utilizada para este problema será a tangente, então:
CO
CO
Tg 30º =
→0,577 =
= 0,577 . 200
200
200
10
AULA
Agora basta adicionar a altura do instrumento para
determinarmos a altura do edifício, portanto temos:
h = 115,4 + 1,5 = 116,9
Sendo assim a alternativa que mais se aproxima da
resposta obtida e a letra c.
a) 112
b) 115
c) 117
d) 120
e) 124
11
DINÂMICA LOCAL INTERATIVA
As estradas AC e AB são asfaltadas. A estrada CB é de
terra e será asfaltada. Sabendo-se que AC tem 30 km, que
o ângulo entre AC e AB é de 30°, e que o triângulo ABC é
retângulo em C, a quantidade de quilômetros da estrada que
será asfaltada é:
B
Use os valores:
sen30° = 0,5
cos30° = 0,866
tg30° = 0,577
A
C
12
AULA
Tabela Trigonométrica
30º
45º
60º
sen
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
3
3
1
3
13
AULA
Exemplo:
Quando o sol se encontra a 45° acima do horizonte, uma
árvore projeta sua sombra no chão com o comprimento
de 15 m. Conforme a ilustração abaixo. Determine a altura
dessa árvore.
45º
15 metros
14
AULA
Resolução: Conforme os dados do problema e a ilustração,
devemos utilizar a razão trigonométrica tangente. Então,
temos:
h
h
Tg 45º=
→1=
→ h = 15.1 = 15
15
15
Resposta 15 metros.
15
DINÂMICA LOCAL INTERATIVA
Agora calcule a altura de uma casa que projeta uma sombra
no chão de 9 metros, sabendo que o sol se encontra 45°
acima do horizonte, conforme a ilustração abaixo:
45o
9 metros
16
RESUMO DO DIA
Canção da Trigonometria
17
RESUMO DO DIA
Função
seno
coseno
tangente
Notação
Definição
sen(x)
medida do cateto oposto
medida da hipotenusa
cos(x)
medida do cateto adjacente a x
medida da hipotenusa
tan(x)
medida do cateto oposto a x
medida do cateto adjacente a x
18
RESUMO DO DIA
Música dos ângulos
19