Aula 4. Trigonometria no Triângulo Retângulo

2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
Aula 4. Trigonometria no Triângulo Retângulo
Definição
Atividades
A trigonometria é o estudo das relações entre lados e
ângulos nos triângulos retângulos. Considere o triângulo
retângulo a seguir.
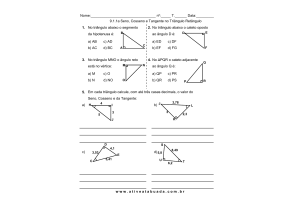
1. Em cada triângulo a seguir, determine o valor do
seno, cosseno e tangente dos ângulos α indicados.
(a)
Todos os triângulos retângulos que têm mesmos ângulos internos são semelhantes a este. As razões de semelhança são chamadas de:
• Seno:
sen x =
medida do cateto oposto a x CO
=
medida da hipotenusa
hip
• Cosseno:
medida do cateto adjacente a x CA
cos x =
=
medida da hipotenusa
hip
(b)
• Tangente:
medida do cateto oposto a x
CO
tg x =
=
medida do cateto adjacente a x CA
Assim, por exemplo, no triângulo anterior, temos:
b
a
c
• cos B̂ =
a
• sen B̂ =
• tg B̂ =
(c)
b
c
Lembre-se que estamos trabalhando com triângulos
retângulos, logo o teorema de pitágoras continua valendo:
a2 = b 2 + c 2
Trigonometria dos ângulos notáveis
2. Um foguete é lançado sob um ângulo de 45° em relação ao solo. Supondo que sua trajetória seja retilínea, qual sua altura quando ele percorreu 4 km?
Ao dividirmos um quadrado ou um triângulo equilátero por uma diagonal ou uma altura, respectivamente,
encontraremos os ângulos de 30◦ , 45◦ e 60◦ . Esses ângulos são chamados de notáveis e, usando as relações definidas, podemos encontrar os seguintes valores:
seno
cosseno
tangente
Professor Podô
30◦
45◦
60◦
1
√2
3
√2
3
3
2
√2
2
2
3
2
1
2
√
1
√
√
3
[email protected]
1
Recuperação Paralela
3. A figura a seguir representa uma árvore de altura
12m. Calcule a sombra s quando um raio luminoso
forma com o solo um ângulo de 60◦ .
2◦ Ano
Tarefa
Em uma folha separada, resolva o exercício 14
da página 219 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
4. Um observador O de altura 1, 75m vê um balão B
sob ângulo de 30◦ em relação ao solo. Em determinado instante, a distância do observador ao balão é
de 146, 50m. Nessas condições:
(a) Desenhe uma figura esquematizando a situação.
(b) Determine a altura h do balão em relação ao
solo.
5. (UFAM-AM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente,
então a tangente do ângulo oposto ao menor lado é:
.
Professor Podô
[email protected]
2